July 18, 2007
Back to 2320AD
The first roleplaying game I gamemastered was 2300AD, the hard science fiction game by GDW. I loved the hard science and the enormous yet well described setting. After a while I knew the 3D coordinates for nearby stars by heart, and I can still feel the extent of the colonisation arms when I look up at the night sky and find the right marker stars.
Perhaps the best idea in the game was the hyperdrive. Rather than allowing ships to travel anywhere at some high speed, it had a finite range. You can only travel 7.7 lightyears before you have to "discharge" the drive near a star or planet. This seemingly simple demand produces a marvellous effect! Instead of spreading out spherically colonies are forced to follow "arms" of locally higher star density. This in turn produces a real sense of geography in the game, with portal systems that can controll access to regions of space, central systems that become trading nexuses and meandering paths around empty regions. Such a simple idea, so many interesting consequences.
The 7.7 lightyear number was of course chosen to produce the right effect. A smaller distance would have limited travel to a small island around the sun, a larger number would have enabled travel anywhere. 7.7 is probably right at the percolation limit. See below for some simulations.
Finally a new version of the game, 2320AD has been published. It builds on the old setting, moving it forward in time by 20 years. This both keeps the continuity and allows the game to change. The somewhat silly cyberpunk GDW introduced has been replaced by a more interesting and sinister control society in the Core and a brewing conflict between transhumanists and "normals". The war against the alien Kafers has been tremendously destructive - it feels good to see that the author is not afraid of wrecking a few worlds and having the humans seriously considering genocide. This also makes the world less squeaky clean than the first and second editions were - now there are colonial seccession attempts, economic hardships and some very dirty political deals. Which of course makes it a fun setting.
I couldn't resist plotting the updated starmap for the 2320 setting. It is also interesting to plot it simply as a topological network. The arms and clusters become even clearer, and the frontiers can be seen extending out from the main arms.
Properly speaking, it is a fictional map because it is based on the first Gliese catalogue: when GDW created the game they used that catalogue, but if newer ones are used the "known" map will change because some star distances were erroneous. Maybe this is the spatial counterpart of an alternate history: an alternate geography.
I like this setting because it is neither soft science space opera nor does it go completely posthuman. It sits on the percolation edge between assuming too little technological change (the computers of the far future are impressively non-impressive) and allowing radical possibilities (some cool material science and biotechnology). That feels much more complex and interesting than allowing or disallowing too much: there is a virtue in limiting a setting so its inhabitants (both purely fictional and player characters) have to spend effort in overcoming it. That makes it like the real world.
I randomly distributed stars with a mean density of 2.34e-3 in a 100 lightyear side cube, and then calculated what fraction of stars were reachable from the midpoint using jumps shorter than a certain range.
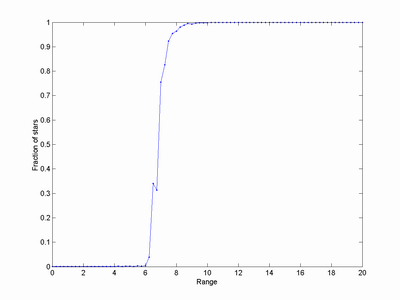
As the range increases we get a typical percolation transition. It seems to happen at 7 lightyears in this run.
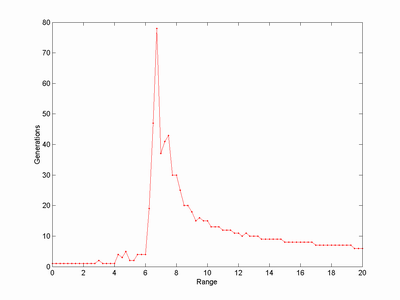
Checking the number of generations needed to find all reachable stars (i.e. the stars reachable from the first one is generation 1, all stars reachable from them not in generation 1 is generation 2, and so on) shows a peak around the transition.
The starmap used in 2300AD is a bit more sparse than the 2.34e-3 number used above; I get 0.0014 stars per cubic lightyear. For that density the critical range is about 8.5 lightyears. Likely the stars are clustered in a nonrandom way to produce the arms. I would expect that there is some theorem in percolation theory that tells us the critical range as a function of density, but I'm not familiar with the literature. The original game authors got a good value, presumably through trial and error.
Posted by Anders3 at July 18, 2007 01:19 AM