Andart

Complex Twisting of Scherk's Surface

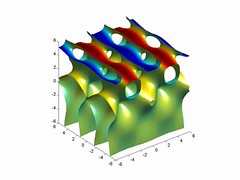Complex Rotation of Sherk's Surface - I did a sequence of how the surface Re(exp(z)cos(x)-cos(y))=0 behaves as real z is replaced with z exp(it). The result is a nice dance as Scherk's minimal surface acquires horizontal planes that squeeze through the small z region, contorting it past a state of rhombic dodecahedra and then over to a 90 degree turned Scherk surface (for t=pi).

I have always liked Scherk's surface. I think it was the first implicit surface I ever plotted, using Maple back in 1991.