May 25, 2011
Why I don't trust Hubbert peak arguments
Recently a post on the Extropians mailing list pointed me to Ugo Bardi's essay "Entropy, peak oil, and Stoic philosophy". Oil, curve fitting, doom and philosophy. What is there not to like?
Lots of data points fitting the curves: good evidence for future predictions, right? Not so fast. It turns out that even something as well behaved as a Gaussian-like curve becomes an unruly beast when trying to fit it with incomplete data.
The basic problem is this: all the lovely curve fits are done to past data where we have the whole sequence from a slow start, exponential increase, peak and then exponential decay. Fitting a curve to a complete data set is very different from fitting it to data that is still arriving: retrodiction is *far* easier than prediction.
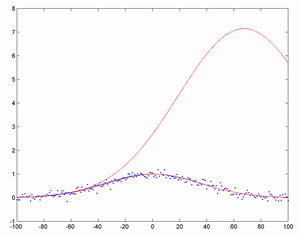
Here is a simple example. I start by taking a Gaussian curve centred on year 0 with a standard deviation of 50 years, with added Gaussian noise of standard deviation 0.1 (i.e. about 10% of the amplitude of the big curve). Then I try fitting a Gaussian to the first N points, and see how well it manages to predict where the peak will be.
The results are pretty bad. At first the fits are all over the place, driven purely by noise. As time goes on, they merely become bad: if you see a roughly exponential increase if is very hard to tell when it is going to stop (the high red curve is based on the first 25% of the data). Eventually, when you have reached the peak (lower red, based on 50% of data), they snap into the right shape and approach the true curve (blue).
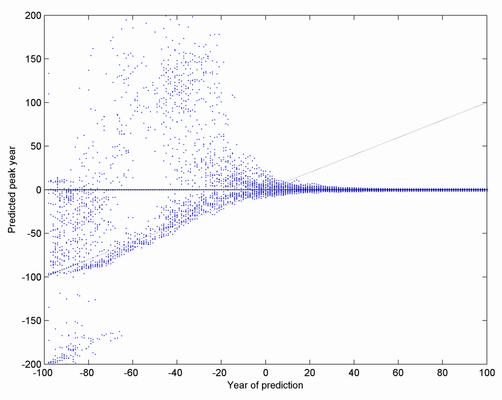
Here is another way of visualizing the results. I plot the predicted peak (y-axis) versus the time the prediction was made (x-axis), for 50 realizations of the noise. As you can see, the predictions are quite worthless until very close to the peak. Afterwards they are just fine, of course. There is also a preponderance in the early days of predictions that the peak is already upon us (the cloud along the diagonal line).
Note that this is an ideal case where the noise is not overwhelming (the problem persists even when I use one tenth as strong noise), the type of curve I am trying to fit actually is the same one as the true one and we have lots of data points with no bias. Reality tends to be worse. Just consider how much selection bias can be introduced by unconsciously picking the right datasets that fit one's theory and discarding the others as 'biased' (especially since you can get nearly any peak by choosing different end dates of your time series). We tend to be overconfident in our ability to predict and remain unbiased.
What to do? The first thing is to stop relying on extrapolated Hubbert peaks as arguments for that we have reached peak oil about now. We can only trust the curve fit if some *other* line of reasoning makes us think we are indeed near or after the peak. Arguments based on other methods are very important - there are plenty of geology, economics, technology and other disciplines that can be brought to bear on the question. In fact, the more *different* lines of evidence are brought to bear on an issue the more reliable the conclusions will be. Past data should feed into rational Bayesian estimation of the real state of the world, but it can be much less powerful than it seems at first glance.
Nice looking retrodictions are not good evidence that predictions will be equally good.
(Edit the 26th May to make conclusions clearer)
Posted by Anders3 at May 25, 2011 05:10 PM