August 30, 2012
My little conjugate minimal surface
In 2006 I found a minimal surface based on the tanh function:
[a,b,c]=Re[tanh(z),i*(2z-tanh(z)), 2ln(cosh(z))].
Maybe not too useful - it is self-intersecting, and since you can get minimal surfaces from the Weierstrass representation from nearly any two functions they are a dime a dozen. But it is still mine (I think).
Today I realized that it had to have a conjugate minimal surface. The Weierstrass representation is the real part of the complex vector function inside the brackets. If you take the imaginary part you get another minimal surface (and by multiplying with exp(it) you can make a seamless morph from one to another).
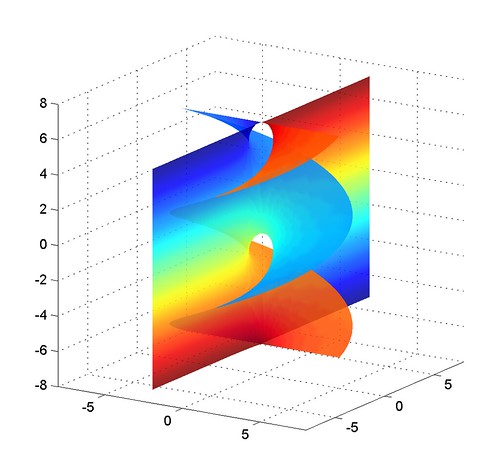
The conjugate of the catenoid is the helicoid. My surface had a lot of catenoid ends, so I suspected it would have helicoid ends. Conjugation also doesn't change the Gauss map (the map to the unit sphere by taking the normal), so I expected the planes to remain. But it was still non-intuitive how the result would look.
The result is fun: it is a surface that has one planar and one helicoidal end. Here are a few pictures:
When plotting it branch cuts matter in order to avoid nasty erroneous triangles. Near Re(z)=0, Im(z)=ąpi/2 the surface blows up into the helicoid: this is literally the counterpart to the catenoid ends of the other surface, each catenoid turning into one period of the helicoid. These pictures make use of the domains Re(z)>0, -pi<Im(z)<pi and Re(z)<0, -pi<Im(z)<pi, avoiding Re(z)=0. Plotting just one domain shows a surface that has a plane end and half a helicoid: those straight lines are places where the surface can be continued using reflection.
