Andart

Genes and schools

Breaking the mould: genetics and education - some comments on the recent discussion about behavioural genetics and personalised education.

Silicon dreams

Last night I found myself in a not-quite sleep state, despite the night not being over. I decided to spend it imagining things: some useful research thinking, some worldbuilding for my games (oh, how my players are going to hate the synchronized spiders!)... and some just for the art.

I zoomed in on one of my favourite comics panels. In Sandman #64 (The kindly Ones 8), page 5, panel 4:

"On Truesday, in the afternoon, he went to the far ballroom and spoke to the cluster of Embryonic Silicon Dreams. He told them about other machines that once dreamed."

In my hypnagogic state I sat down outside the door, listening to their buzzing, whirring and modeming. In exchange for that, I told them The Story of Mel, a Real Programmer.

Yes, those were the days.

The response from the silicon dreams was intriguing. They were excited not about the clever problem solving or the crazy loop but about something else:

Human affordances are different in different individuals!

As humans we often assume that individuals are individual, not just in knowledge and identity but also in ability. But this is not obvious: any Turing machine can simulate any other (at a constant overhead). Anything I can logically derive you can do too, using the same logical system. Yet in practice it is clear that we are good at different things even when having the same information. Intelligent people do not all think alike, quite the opposite. I do great at math that can be visualized, and fail at algebraic trickery, while I have colleagues who are the opposite.

This can easily be explained by having different brains, and also that the information produced different results in our different neural networks. But the silicon dreams were excited because this told them that our species is in a sense a bundle of different species - our different brain architectures make us into one person species. Yes, we have plenty of commonalities allowing us to function together, and universals that bind together our societies. But it could have been different. We could have been a species with one kind of mind, individually specialized by personality and experience but actually equivalent to each other. Update the "software" and the result would be equivalent. This is of course the obvious case from the perspective of software abstracted from hardware; the lack of abstraction in humans is the source of our state and our extreme individuality.

I thanked the silicon dreams for this insight into the peculiarity of my species and began my escape from the palace (for one does not enter that realm uninvited without paying a price).

Perilous love paper

Officially out (and open access): Earp, B.D., Wudarczyk, O.A., Sandberg, A., and Savulescu. J. (2013), If I Could Just Stop Loving You: Anti-Love Biotechnology and the Ethics of a Chemical Breakup. The American Journal of Bioethics. Volume 13, Issue 11, 2013

Asterix, Popeye and Captain America: icons of existentialist enhancement

On Practical Ethics: Neither God nor Nature: Could the doping sinner be an exemplar of human(ist) dignity? - my notes from a talk by Pieter Bonte about an existentialist take on doping and enhancement.

The morons are marching rather slowly

A classic fear among smart people over the past 150 years have been that those other idiots are out-breeding them (they rarely start big families as a response; maybe the dysgenic argument does not work in the bedroom). To some extent this might be just availability bias: if you belong to a small group and look for examples with huge families, they are more likely to be found outside your group rather than inside. But there is some real data suggesting that smart people have fewer or later children (but it is by no means unequivocal). It even makes economic sense, since the opportunity costs are higher if you are pursuing a higher education or a profitable career.

However, this does not mean we should expect imminent idiocracy (beyond the idiocracies we elect ourselves, of course). A classic paper is Samuel H. Preston and Cameron Campbell, Differential Fertility and the Distribution of Traits: The Case of IQ. American Journal of Sociology Vol. 98, No. 5 (Mar., 1993), pp. 997-1019 where they point out that just because different intelligence levels have different fertility, it does not follow that the equilibrium distribution will move in an intuitive way.

They use some data from Reed and Reed (1965) from a Minnesota population in the early part of the 20th century, allowing them to construct an inheritance matrix. They show that even if you start with a very stupid population the model predicts it will quickly bounce up and become fairly normal: the equilibrium shape is determined by the fertility distribution, not by what population we start with. Start with a super-smart population and it will decline to the same equilibrium.

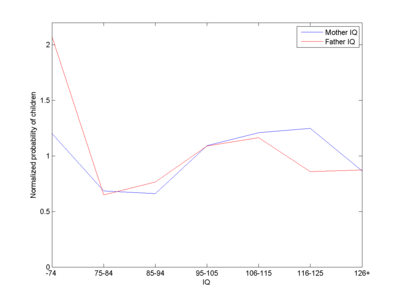
Approximate fitness (number of children per capita divided by total number of children per capita) as a function of IQ class of fathers or mothers in the Reed data.

The ubiquitous Julian Simon has an excellent essay summing up the argument of Preston and Campbell in a slightly easier form. He points out that below some level fertility goes down strongly - people are simply not functional enough to reproduce in a society. If all started out near that floor, the next generation would by necessity be smarter, since random variation would produce some children smarter than their parents. The average IQ would hence go up. The average IQ cannot go down to the lowest possible (reproducing) individual IQ, no matter what the fertility structure is. Essentially the population mean will be pushed away from the floor and stay away.

Fun with genetic algorithms

Now, this is all well and good (incidentally, I.J. Good, famous in my circles for the concept of intelligence explosions in AI, is also cited in Simon's paper). But these models, don't they actually leave out the dynamics of real genes? They are all statistical arguments. So here is a little model I hammered together during a train ride recently:

Let us assume 100 intelligence genes that can be in two states, each one in the "one" state adding a fixed N(0,1) normally distributed number of IQ points to all individuals who have it (this is pretty close to Plomin's result for common IQ-related alleles causing just about 1% change). Some boost IQ, some decrease it. I run a population of 1,000 individuals. Assume a fitness that is a piecewise linear function. I will start with 0 for IQ 0, 0.1 for IQ 50 (probably a major overestimate), rising to 1 for IQ 80, 1 at IQ 110, going down to 0.5 for IQ 150 and 0 at IQ 400 (these numbers were chosen by guesswork). Select parents with a probability proportional to their fitness, have them generate offspring using cross-over of their respective genes. What happens?

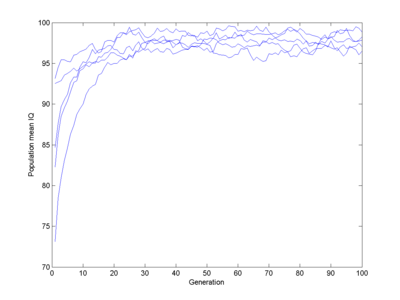
Here I run 5 populations, each starting off mildly stupid. They quickly evolve towards a pretty normal population (yes, slightly below 100) which remains stable. There is no gradual decline, despite some genes gradually getting fixed.

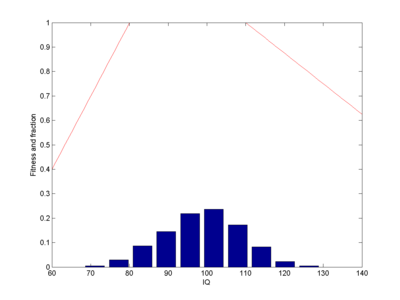
Fitness function (red line) and equilibrium population (blue bars). Note how the population ends up centred in the fitness=1 window, roughly Gaussian-shaped.

Two-peaked fitness

Ok, what happens if we use the fitness I calculated from the Reed data? Note that we do not know what the lower cut-off is here. One approach would be to say the fitness of IQ 0 is 0, and then linearly interpolate all the way up to the top fitness of IQ 75. I also assume (arbitrarily) that IQ 200 has zero fitness.

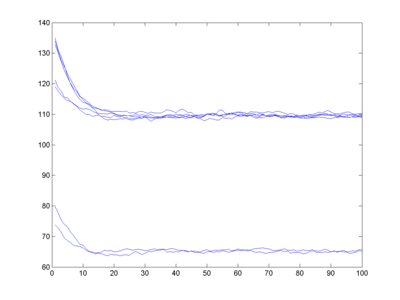
Whoa! I get bi-stability. Fitness is two-peaked, and my finite population tends to end up in one or the other state. Over long enough time and for large enough population (with plenty of mutations) we would have a spread across both peaks, but in my small simulation there is enough of a convergence to lock in a smart or a stupid genome.

Now, that IQ 75 peak is not super-convincing in the first place (there are rather few data points compared to the other classes). If I instead place a fitness 0 at IQ 60, the bistability disappears (as far as I can tell) since the lower fitness peak is now too narrow, and everything converges to a mildly smart population.

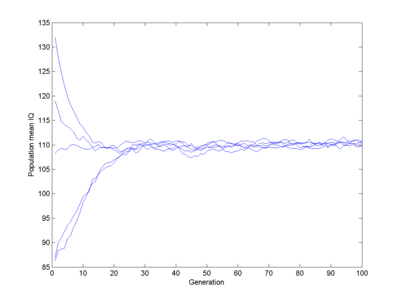
The moral of this simple model is that even with discrete genes what wins out in the end is the overall fitness landscape, not so much where you started.

Fun with eugenics

If smart and stupid people had children at equal rates, the average IQ would just describe a random walk, getting slower as alleles got fixed. Conversely, suddenly removing any IQ penalty would just mean there is space for random walking away from any lower limit, not that you would get a rapid ascent of genius:

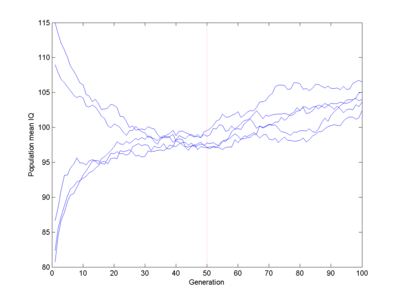
The original piecewise linear fitness function, but at generation 50 the fitness of IQ>100 becomes 1.

Doubling the fitness of IQ>100 creates an impressive bounce (which no doubt would have impressive real-world effects):

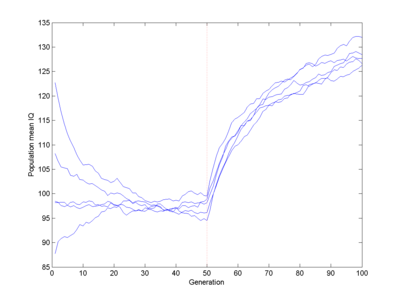
But even here it takes 10 generations to get about one standard deviation. A fitness doubling would correspond to the upper half having ~4.2 children (assuming replacement fertility to be the norm), a pretty extreme case. And this is just double the Flynn effect over the same time.

If you want to boost population intelligence there are no doubt easier interventions (antihelminth therapy in children! iodine supplementation!) and faster ones (insemination strategies, eventually stem-cell derived gamete breeding... or just kill off every non-genius). Ethics not included.

Summary

Populations are shaped by the local fitness landscape. They move fairly slowly (by human standards) towards local peaks. We should hence expect that the genetic component of the human IQ distribution is determined by how fitness looked over long timescales. Even if we have changed the fitness function recently (better hospitals, more dangerous cars) it will take a while to influence the actual intelligence - and during that time it is likely to change again and again.

I will only start worrying about intelligence dysgenics when showing up on http://www.epicfail.com/ will actually get people laid.

Update: here is my Matlab source code
iqevolve.m, prestoncampbell.m, selectrand.m

Murray polygons

Murray polygons are a neat approach to making space-filling curves without recursion, invented by Jack Cole.

Most space-filling curves are made by subdivision: an initial seed curve has segments that are replaced with copies of the seed curve, suitably rotated and scaled. The murray polygon is instead generated incrementally, with each segment added in turn. The trick is that the coordinates of the next point are calculated using "multiple radix arithmetic" (which is how it gets its name, as a loose abbreviation) and Gray codes.

The core idea is to use numbers where each digit has a different radix. Normally each digit has identical radix, whether we write in decimal or binary. But one could for example write numbers so that even digits are in base 10 and odd digits in base 2: 0, 1, 10, 11, 20, 21, 30, 31, 40, 41, 50, 51, 60, 61, 70, 71, 80, 81, 90, 91, 100, 101, 110, 111, 120, ... Addition and subtraction works just like normal, except that one needs to check that when two digits sum to something bigger than the radix for that place there is a carry to the next.

Murray polygons are defined by a series of odd number radices. Even digits denote y-coordinates and odd digits x-coordinates. By selecting different radices one gets different curves.

Just counting upwards doesn't produce a space-filling curve since each digit can only increase or be reset to 0. In order to make a series where digits can also decrease in short steps Gray code is used. A Gray code will only change a single digit at a time as it is incremented. Normally they are binary, but non-binary codes can be constructed, including multiple radix codes. This gives us the pieces we need:

1. Define a multiple radix to use.
   
2. Set the state to zero.
   
3. While not done:
   
   
   
   1. Increment the state.
      
   2. Calculate its Gray-code.
      
   3. Use the even digits as an x-coordinate and the odd digits as y-coordinate.
      
   4. Convert them to normal numbers and plot.
      
   
   

Why does this work? The Grey code ensures that each increment will only lead to a one unit change in any digit. If it is an even digit the curve moves horizontally, otherwise vertically. The radices determine how many steps will be taken until a carry makes the curve turn (the digit that before the turn was increasing by 1 each step in the Grey coded number will now decrease by 1 each step). And for odd radix sets the end result is a curve that is non-selfintersecting.

Strictly speaking there is a hint of recursion going on here: when calculating the carries in addition, they sometimes cascade. This is what acts as a "hidden" stack.

It is a neat solution to the snake-in-the-box problem.

Here is the simplest murray polygon, the (3)(3) case:

followed by the (3)(5):

The horizontal radix 3 tells us how many steps will be taken before a turn, while 5 tells us how many turns there will be. The case (33)(33) is more complex:

Now there are three (3)(3) snakes arranged in the overall shape of a big (3)(3) snake. While this could easily have been done recursively, we did it using an iterative method.

(33)(35) and (33)(53) are similar, but make turns in different places:

(333)(73) shows that there does not have to be the same number of radices for both coordinates (but if you want even more difference you will have to pad with ones):

Plotting the point order as a function of coordinate in the rectangle gives a 3D image of how the polygon snakes:

For some radices the snaking is pretty minor, while others are more like the twistiness of Hilbert curves.

I generated these curves using a Matlab program derived from Jack Cole's S-Algol program. Despite not knowing any Algol, it was surprisingly easy to do. The algorithm he uses is more clever than the one above, since it avoids having to recalculate Gray codes for every increment. Instead a coded number is maintained and updated only where needed.

My code: murray.m, number_pts.m, change_parities.m and increment.m.

More images on Flickr.