October 19, 2013
The morons are marching rather slowly
A classic fear among smart people over the past 150 years have been that those other idiots are out-breeding them (they rarely start big families as a response; maybe the dysgenic argument does not work in the bedroom). To some extent this might be just availability bias: if you belong to a small group and look for examples with huge families, they are more likely to be found outside your group rather than inside. But there is some real data suggesting that smart people have fewer or later children (but it is by no means unequivocal). It even makes economic sense, since the opportunity costs are higher if you are pursuing a higher education or a profitable career.
However, this does not mean we should expect imminent idiocracy (beyond the idiocracies we elect ourselves, of course). A classic paper is Samuel H. Preston and Cameron Campbell, Differential Fertility and the Distribution of Traits: The Case of IQ. American Journal of Sociology Vol. 98, No. 5 (Mar., 1993), pp. 997-1019 where they point out that just because different intelligence levels have different fertility, it does not follow that the equilibrium distribution will move in an intuitive way.
They use some data from Reed and Reed (1965) from a Minnesota population in the early part of the 20th century, allowing them to construct an inheritance matrix. They show that even if you start with a very stupid population the model predicts it will quickly bounce up and become fairly normal: the equilibrium shape is determined by the fertility distribution, not by what population we start with. Start with a super-smart population and it will decline to the same equilibrium.
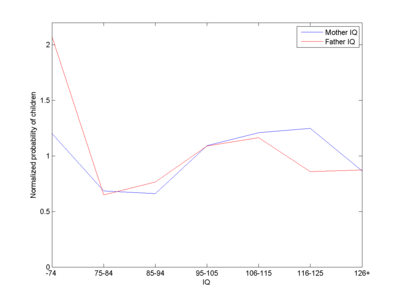
Approximate fitness (number of children per capita divided by total number of children per capita) as a function of IQ class of fathers or mothers in the Reed data.
The ubiquitous Julian Simon has an excellent essay summing up the argument of Preston and Campbell in a slightly easier form. He points out that below some level fertility goes down strongly - people are simply not functional enough to reproduce in a society. If all started out near that floor, the next generation would by necessity be smarter, since random variation would produce some children smarter than their parents. The average IQ would hence go up. The average IQ cannot go down to the lowest possible (reproducing) individual IQ, no matter what the fertility structure is. Essentially the population mean will be pushed away from the floor and stay away.
Fun with genetic algorithms
Now, this is all well and good (incidentally, I.J. Good, famous in my circles for the concept of intelligence explosions in AI, is also cited in Simon's paper). But these models, don't they actually leave out the dynamics of real genes? They are all statistical arguments. So here is a little model I hammered together during a train ride recently:
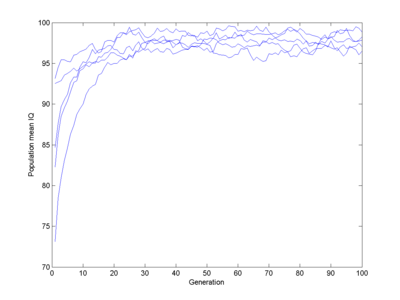
Let us assume 100 intelligence genes that can be in two states, each one in the "one" state adding a fixed N(0,1) normally distributed number of IQ points to all individuals who have it (this is pretty close to Plomin's result for common IQ-related alleles causing just about 1% change). Some boost IQ, some decrease it. I run a population of 1,000 individuals. Assume a fitness that is a piecewise linear function. I will start with 0 for IQ 0, 0.1 for IQ 50 (probably a major overestimate), rising to 1 for IQ 80, 1 at IQ 110, going down to 0.5 for IQ 150 and 0 at IQ 400 (these numbers were chosen by guesswork). Select parents with a probability proportional to their fitness, have them generate offspring using cross-over of their respective genes. What happens?
Here I run 5 populations, each starting off mildly stupid. They quickly evolve towards a pretty normal population (yes, slightly below 100) which remains stable. There is no gradual decline, despite some genes gradually getting fixed.
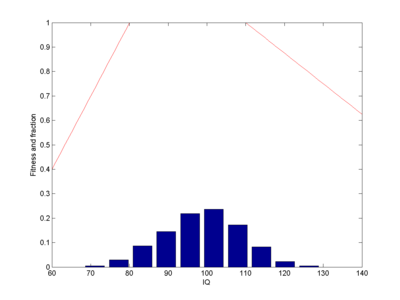
Fitness function (red line) and equilibrium population (blue bars). Note how the population ends up centred in the fitness=1 window, roughly Gaussian-shaped.
Two-peaked fitness
Ok, what happens if we use the fitness I calculated from the Reed data? Note that we do not know what the lower cut-off is here. One approach would be to say the fitness of IQ 0 is 0, and then linearly interpolate all the way up to the top fitness of IQ 75. I also assume (arbitrarily) that IQ 200 has zero fitness.
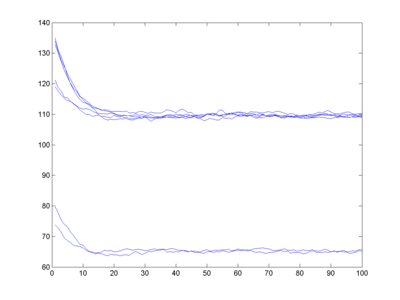
Whoa! I get bi-stability. Fitness is two-peaked, and my finite population tends to end up in one or the other state. Over long enough time and for large enough population (with plenty of mutations) we would have a spread across both peaks, but in my small simulation there is enough of a convergence to lock in a smart or a stupid genome.
Now, that IQ 75 peak is not super-convincing in the first place (there are rather few data points compared to the other classes). If I instead place a fitness 0 at IQ 60, the bistability disappears (as far as I can tell) since the lower fitness peak is now too narrow, and everything converges to a mildly smart population.
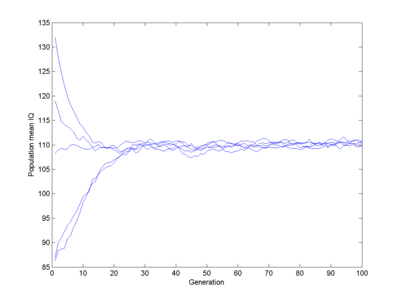
The moral of this simple model is that even with discrete genes what wins out in the end is the overall fitness landscape, not so much where you started.
Fun with eugenics
If smart and stupid people had children at equal rates, the average IQ would just describe a random walk, getting slower as alleles got fixed. Conversely, suddenly removing any IQ penalty would just mean there is space for random walking away from any lower limit, not that you would get a rapid ascent of genius:
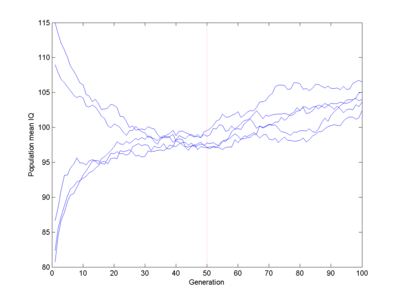
The original piecewise linear fitness function, but at generation 50 the fitness of IQ>100 becomes 1.
Doubling the fitness of IQ>100 creates an impressive bounce (which no doubt would have impressive real-world effects):
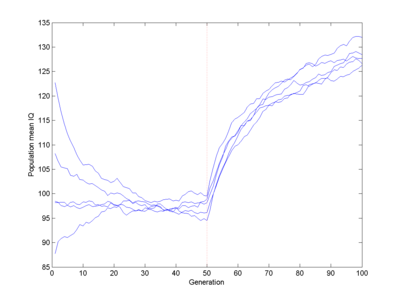
But even here it takes 10 generations to get about one standard deviation. A fitness doubling would correspond to the upper half having ~4.2 children (assuming replacement fertility to be the norm), a pretty extreme case. And this is just double the Flynn effect over the same time.
If you want to boost population intelligence there are no doubt easier interventions (antihelminth therapy in children! iodine supplementation!) and faster ones (insemination strategies, eventually stem-cell derived gamete breeding... or just kill off every non-genius). Ethics not included.
Summary
Populations are shaped by the local fitness landscape. They move fairly slowly (by human standards) towards local peaks. We should hence expect that the genetic component of the human IQ distribution is determined by how fitness looked over long timescales. Even if we have changed the fitness function recently (better hospitals, more dangerous cars) it will take a while to influence the actual intelligence - and during that time it is likely to change again and again.
I will only start worrying about intelligence dysgenics when showing up on http://www.epicfail.com/ will actually get people laid.
Update: here is my Matlab source code
iqevolve.m, prestoncampbell.m, selectrand.m