April 17, 2014
Tables of Soyga: the first cellular automaton?
Was the first cellular automaton intended to do encryption and/or summon angels?
Normally the history of cellular automata begins with von Neumann’s classical study of self-replicating systems in the 1950s. While clearly influenced by Turing’s discrete automata, this was the first paper using a grid of cells in different states where each cell changed each clock tick according to a fixed, universal rule. Even Stephen Wolfram seems to think so: "Despite their very simple construction, nothing like general cellular automata appear to have been considered before about the 1950s."
But maybe von Neumann was scooped by a few centuries.
Liber Soyga
Liber Soyga is a early modern book. It was owned by Dr John Dee, the Elizabethan scholar, magician and government adviser (check out Leslie A. Rutledge's entertaining "John Dee: Consultant to Queen Elizabeth I"). He mentioned it in a few locations, but the identity of the work was lost for many years. In 1994 Deborah Harkness managed some nice scholarly sleuthing and found copies at the Oxford Bodleian Library and the British Library (filed under an alternative, non-obvious title).
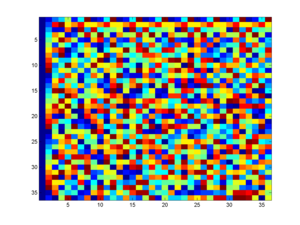
The work contains various pieces of astrology, cabalism, lists of supernatural names and summoning formulas. At the end there are 36 36x36 squares of apparently random letters, labelled by the constellations (twice), planets, elements and the word "magistri".
An example is the first square of Aries:
ndizbdizbdizbdizbdizbdizbdizbdizbdiz
isrlytrlytrlytrlytrlytrlytrlytrlytrl
scucbxibaxibaxibaxibaxibaxibaxibaxib
roernmhggdokqsrnplfdfzlyqsrnplfdfzly
aqbtxdnxytybscuefnutohqtauiducisohqt
mppimcqsgbadzelbhsekfkhaczlaysrfqegb
mozlirdziqxthkceykubhpxqzbnpmreuhkyr
aqucmqablnmsqgitgqrnygdxppcsuiteybat
rdbectiqhsukhmhaigzpmffzrcfumhageqxl
smagikasqpkbkdnpyypeciupgiumlepuuhco
icdmhpoctzmamcqmxozgizygnzydqbrhbksy
nrpbkgusdecdroaofquyabaidensadyzdphd
nhurxymrpslatyqlctenpporpsxkqaabfrtm
iymqsgsbrfnpingrodkefrbtzunasipptbxd
sgsauykreueflkyiessnuiqqummzuarcyris
rscdbamqbyuxcnnzgauelfsaydrlrmqzatrf
ausmacpfddbzedshmzyuciipmcucudxpodyx
mtcpolmesmabgkkzohdbezlmlzysesfrbfaz
mslmnbonicdgnamyfktkupaothdzgahyrrmy
aucpceedolaidfogmikbygguleshmzkobtuo
rhhusntmnbcmciexdoskopumkukzohpdgbyf
sqelpcydsksusrqsmniaqmtubybbqeffiqto
iglhusgkkbumregaoxactulrnnqyhkxxasdt
nxclrfiamaydyuyqlsirgcobpctgosfzcxtd
nmbnhlfcpogkoengrflopqlygikyfuxpqsdi
icednbhhufiaqbpuiucrcttgnzmxxmugyktr
slbfppxzyxactkgcmtlolqqdshrimlrsgqqo
ryrrcsfbazcfxbirzxcryhxtclorznhzigyf
aatbeiurmysofdobbzehdnmslhtbbpxpyyoo
mzxrqfyicbufhieqypsqapbuclqyrcarkoyf
mynhxxorokmeyagyozuhfrnlzngehhftsyoo
aapxnmnhtsuuoixoypkzhyebbpuuzkxlpmne
rmofpbpxlpkmnzzqtzmyzaghgxmthplhudsn
sufhurcanfmlkpngbbogfckzimlqefnymcxe
ilclrermmecoszpurnexxsshouctnuencfzg
nbebtnhrzgieiozyidknmrfkfysdsetxsohm
This is similar to many other early modern magical books: John Dee is himself famous among hermeticists for his "Enochian squares". Exactly how the Soyga squares were to be used is apparently unclear; Dee himself tried asking the archangel Uriel if the book was any good but got told that it was above his clearance.
The next step of the story is that the Soyga squares were reverse engineered by Jim Reeds. He found the rule to generate them: a keyword is used to seed the left edge (the word is written downwards, followed by itself in reverse, in the right order, reverse, and so on - in the above example the word is "nisram"). Each cell depends on the cell to the left and above itself: the letter to the left determines how many steps forward in the alphabet to move from the letter above.
L(i,j)= [L(i-1,j)+f(L(i,j-1))] mod 23, if L(i,j) is the letter in row i and column j. f() is an apparently arbitrary list of values. The top row is generated by L(1,j)= [L(1,j-1)+f(L(1,j-1))] mod 23, taking the left letter as the top letter too.
Plotting the result as color rather than letters gives the following pattern:
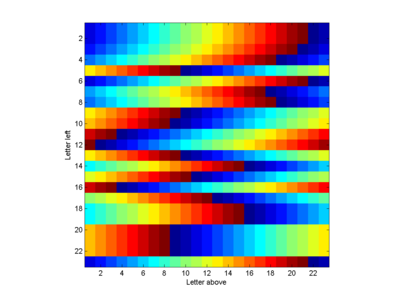
The Soyga Automaton
The cool thing is that this is essentially a 23 state 1D cellular automaton, where the time is running from the left to the right.
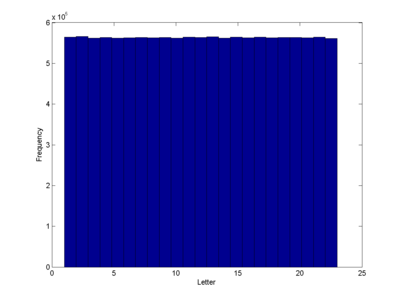
The dynamics is strongly chaotic (class 3), producing an apparently random distribution of letters. There is a slight bias because of the top boundary condition: there are two attractor states along the top, one consisting of repetitions of ”dizb” and one of repetitions of “oy”. The oy attractor tends to produce a triangle of repeated “oy”. But even if the keyword is just "a" the pattern is chaotic (as demonstrated in the image at the top).
Using this kind of rule generically produces pseudorandom behavior: nearly any transition table f() will work. Some have triangle slices along the top of repeating patterns, but most seem to approach an even distribution of letter frequency.
That the dynamics is generically random for many-state automata is well known.
It is less obvious that it would also generate an even distribution of states. However, if one looks at the transition table T(i,j) denoting what letter one gets from having letters i and j to the left and above the uniformity becomes more obvious: each row is a circular shift of the alphabet, so the total number of instances of each resulting letter is the same. A random transition matrix would have produced some letters more often than others. There is still the issue that some matrices like these might have subsets of letters permuted to each other (imagine one where even letters are turned into even letters and odd ones into odd), so some keywords would induce an uneven distribution. But presumably ergodicity is generic for this class of automata.
What was it good for?
Why did the originator invent this rule? Reeds compares it to other letter tables from the same era, and it is pretty clear that Soyga is indeed far more advanced than the other tables. Most have very simple repeating or zigzagging patterns. Rutledge notes that some of Dee’s tables had crudely random patterns reminiscent of a person filling them in by hand in an arbitrary way.
Most of these tables were intended for magical use: to make talismans or find sacred names in order to perform magical invocations of angels.
However, I wonder if the purpose was cryptographic: the medieval and early modern ciphers made use of tables of rectification. Trithemius Steganographia is mentioned in Soyga, and is itself an apparent treatise on magic that actually does contain cryptographic work.
Hiding a cipher key in the form of a magical table would seem fairly rational as a cover today, but given how much more sensitive magic was back then (it landed both Trithemius and Dee in trouble) it is a bit like using illegal pornography as a way of hiding encryption keys: not exactly a discreet method if somebody pries.
Soyga might have been a method of generating new tables that were far more random than the Trithemius table. It produces an uniform distribution of letters with nearly no pattern. Take the first 23 rows and columns as a tabula recta and you have something that would be far more resistant to cryptoanalysis.
But given that the Vigenčre cipher was viewed as uncrackable, was there a perceived need for anything else? I suspect that the urge to invent new encryption methods has always been strong: if you have a cool idea based on your own field of expertise, you will suggest it (after all, if you cannot break it, it must be unbreakable!).
In fact, the use of a transformation of the previous column seems to be like an autokey cipher. The first real autokey cipher was suggested ion 1556 by Cardano in De Subtilitate, but the first useful on was invented in 1564 by Giovan Battista Bellaso. Vigenčre published one in 1586. Liber Soyga was mentioned by Dee in 1583. Could the Soyga automaton be the result of somebody working on an autokey method, perhaps getting the bright idea of applying it again and again to itself? It would seem to fit into the time.
Of course, the border between cryptography and angelic communication might have been blurry. Maybe the tables were seen as both: sufficiently advanced cryptography is indistinguishable from magic.