analysis

Some math for Epiphany

Analytic functions helping you out

Recently I chatted with a mathematician friend about generating functions in combinatorics. Normally they are treated as a neat symbolic trick: you have a sequence a_n (typically how many there are of some kind of object of size n), you formally define a function f(z)=\sum_{n=0}^\infty a_n z^n, you derive some constraints on the function, and from this you get a formula for the a_n or other useful data. Convergence does not matter, since this is purely symbolic. We used this in our paper counting tie knots. It is a delightful way of solving recurrence relations or bundle up moments of probability distributions.

I innocently wondered if the function (especially its zeroes and poles) held any interesting information. My friend told me that there was analytic combinatorics: you can actually take f(z) seriously as a (complex) function and use the powerful machinery of complex analysis to calculate asymptotic behavior for the a_n from the location and type of the “dominant” singularities. He pointed me at the excellent course notes from a course at Princeton linked to the textbook by Philippe Flajolet and Robert Sedgewick. They show a procedure for taking combinatorial objects, converting them symbolically into generating functions, and then get their asymptotic behavior from the properties of the functions. This is extraordinarily neat, both in terms of efficiency and in linking different branches of math.

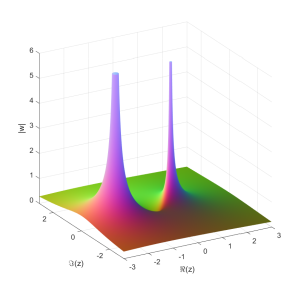
Plot of z/(1-z-z^2), the generating function of the Fibonacci numbers. It has poles at (1+sqrt(5))/2 (the dominant pole giving the overall asymptotic growth of Fibonacci numbers) and (1-sqrt(5))/2, which does not contribute much to the asymptotic behavior.
Plot of z/(1-z-z^2), the generating function of the Fibonacci numbers. It has poles at (1+sqrt(5))/2 (the dominant pole giving the overall asymptotic growth of Fibonacci numbers) and (1-sqrt(5))/2, which does not contribute much to the asymptotic behavior.

In our case, one can show nearly by inspection that the number of Fink-Mao tie knots grow with the number of moves as \sim 2^n, while single tuck tie knots grow as \sim \sqrt{6}^n.

Analytic functions behaving badly

The second piece of math I found this weekend was about random Taylor series and lacunary functions.

If f(z)=\sum_{n=0}^\infty X_n z^n where X_n are independent random numbers, what kind of functions do we get? Trying it with complex Gaussian X_n produces a disk of convergence with some nondescript function on the inside.

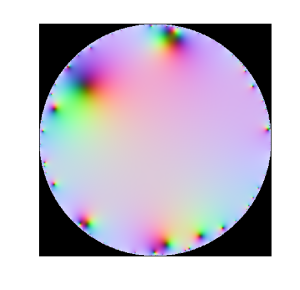
Plot of function with a Gaussian Taylor series. Color corresponds to stereographic mapping of the complex plane to a sphere, with infinity being white and zeros black. The domain of convergence is the unit circle.
Plot of function with a Gaussian Taylor series. Color corresponds to stereographic mapping of the complex plane to a sphere, with infinity being white and zeros black. The domain of convergence is the unit circle.

Replacing the complex Gaussian with a real one, or uniform random numbers, or even power-law numbers gives the same behavior. They all seem to have radius 1. This is not just a vanilla disk of convergence (where an analytic function reaches a pole or singularity somewhere on the boundary but is otherwise fine and continuable), but a natural boundary – that is, a boundary so dense with poles or singularities that continuation beyond it is not possible at all.

The locus classicus about random Taylor series is apparently Kahane, J.-P. (1985), Some Random Series of Functions. 2nd ed., Cambridge University Press, Cambridge.

A naive handwave argument is that for |z|<1 we have an exponentially decaying sequence of z^n, so if the X_n have some finite average size E(X) and not too divergent variance we should expect convergence, while outside the unit circle any nonzero E(X) will allow it to diverge. We can even invoke the Markov inequality P(X>t) \leq E(X)/t to argue that a series \sum X_n f(n) would converge if \sum f(n)/n converges. However, this is not correct enough for proper mathematics. One entirely possible Gaussian outcome is X_n=1,10,100,1000,\ldots or worse. We need to speak of probabilistic convergence.

Andrés E. Caicedo has a good post about how to approach it properly. The “trick” is the awesome Kolmogorov zero-one law that implies that since the radius of convergence depends on the entire series X_n rather than any finite subset (and they are all independent) it will be a constant.

This kind of natural boundary disk of convergence may look odd to beginning students of complex analysis: after all, none of the functions we normally encounter behave like this. Except that this is of course selection bias. If you look at the example series for lacunary functions they all look like fairly reasonable sparse Taylor series like $z+z^4+z^8+z^16+^32+\lddots$. In calculus we are used to worrying that the coefficients in front of the z-terms of a series don’t diminish fast enough: having fewer nonzero terms seems entirely innocuous. But as Hadamard showed, it is enough that the size of the gaps grow geometrically for the function to get a natural boundary (in fact, even denser series do this – for example having just prime powers). The same is true for Fourier series. Weierstrass’ famous continuous but nowhere differentiable function is lacunary (in his 1880 paper on analytic continuation he gives the example \sum a_n z^{b^n} of an uncontinuable function). In fact, as Emile Borel found and Steinhardt eventually proved in a stricter sense, in general (“almost surely”) a Taylor series isn’t continuable because of boundaries.

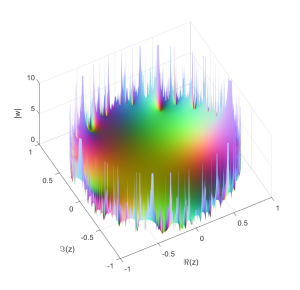
The function sum_p z^p, where p runs over the primes.
The function [latex]sum_p z^p[/latex], where [latex]p[/latex] runs over the primes.

One could of course try to combine the analytic combinatorics with the lacunary stuff. In a sense a lacunary generating function is a worst case scenario for the singularity-measuring methods used in analytical combinatorics since you get an infinite number of them at a finite and equal distance, and now have to average them together somehow. Intuitively this case seems to correspond to counting something that becomes rarer at a geometric rate or faster. But the Borel-Steinhardt results suggest that even objects that do not become rare could have nasty natural boundaries – if the number a_n were due to something close enough to random we should expect estimating asymptotics to be hard. The funniest example I can think of is the number of roots of Chaitin-style Diophantine equations where for each n it is an independent arithmetic fact whether there are any: this is hardcore random, and presumably the exact asymptotic growth rate will be uncomputable both practically and theoretically.