How much should we spread out across future scenarios?

Robin Hanson mentions that some people take him to task for working on one scenario (WBE) that might not be the most likely future scenario (“standard AI”); he responds by noting that there are perhaps 100 times more people working on standard AI than WBE scenarios, yet the probability of AI is likely not a hundred times higher than WBE. He also notes that there is a tendency for thinkers to clump onto a few popular scenarios or issues. However:

In addition, due to diminishing returns, intellectual attention to future scenarios should probably be spread out more evenly than are probabilities. The first efforts to study each scenario can pick the low hanging fruit to make faster progress. In contrast, after many have worked on a scenario for a while there is less value to be gained from the next marginal effort on that scenario.

This is very similar to my own thinking about research effort. Should we focus on things that are likely to pan out, or explore a lot of possibilities just in case one of the less obvious cases happens? Given that early progress is quick and easy, we can often get a noticeable fraction of whatever utility the topic has by just a quick dip. The effective altruist heuristic of looking at neglected fields also is based on this intuition.

A model

But under what conditions does this actually work? Here is a simple model:

There are $N$ possible scenarios, one of which ( $j$ ) will come about. They have probability $P_i$ . We allocate a unit budget of effort to the scenarios: $\sum a_i = 1$ . For the scenario that comes about, we get utility $\sqrt{a_j}$ (diminishing returns).

Here is what happens if we allocate proportional to a power of the scenarios, $a_i \propto P_i^\alpha$ . $\alpha=0$ corresponds to even allocation, 1 proportional to the likelihood, >1 to favoring the most likely scenarios. In the following I will run Monte Carlo simulations where the probabilities are randomly generated each instantiation. The outer bluish envelope represents the 95% of the outcomes, the inner ranges from the lower to the upper quartile of the utility gained, and the red line is the expected utility.

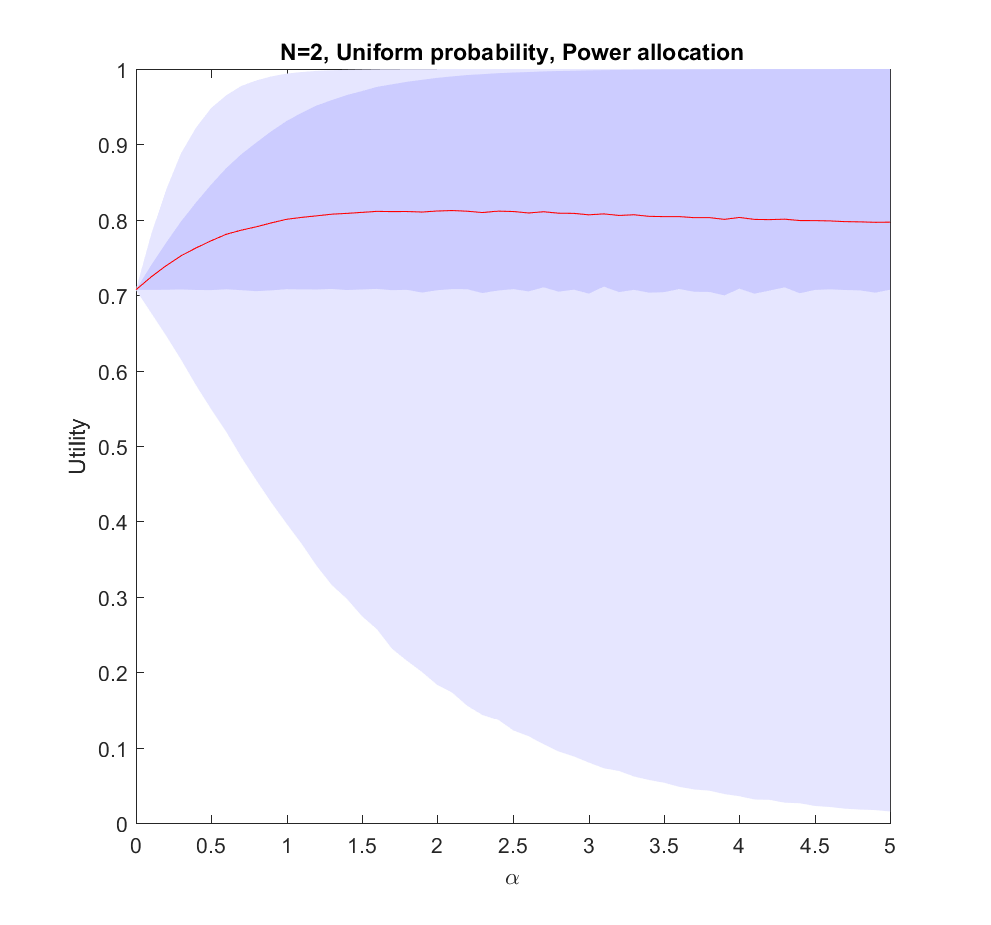
Utility of allocating effort as a power of the probability of scenarios. Red line is expected utility, deeper blue envelope is lower and upper quartiles, lighter blue 95% interval.

This is the $N=2$ case: we have two possible scenarios with probability $p$ and $1-p$ (where $p$ is uniformly distributed in [0,1]). Just allocating evenly gives us $1/\sqrt{2}$ utility on average, but if we put in more effort on the more likely case we will get up to 0.8 utility. As we focus more and more on the likely case there is a corresponding increase in variance, since we may guess wrong and lose out. But 75% of the time we will do better than if we just allocated evenly. Still, allocating nearly everything to the most likely case means that one does lose out on a bit of hedging, so the expected utility declines slowly for large $\alpha$ .

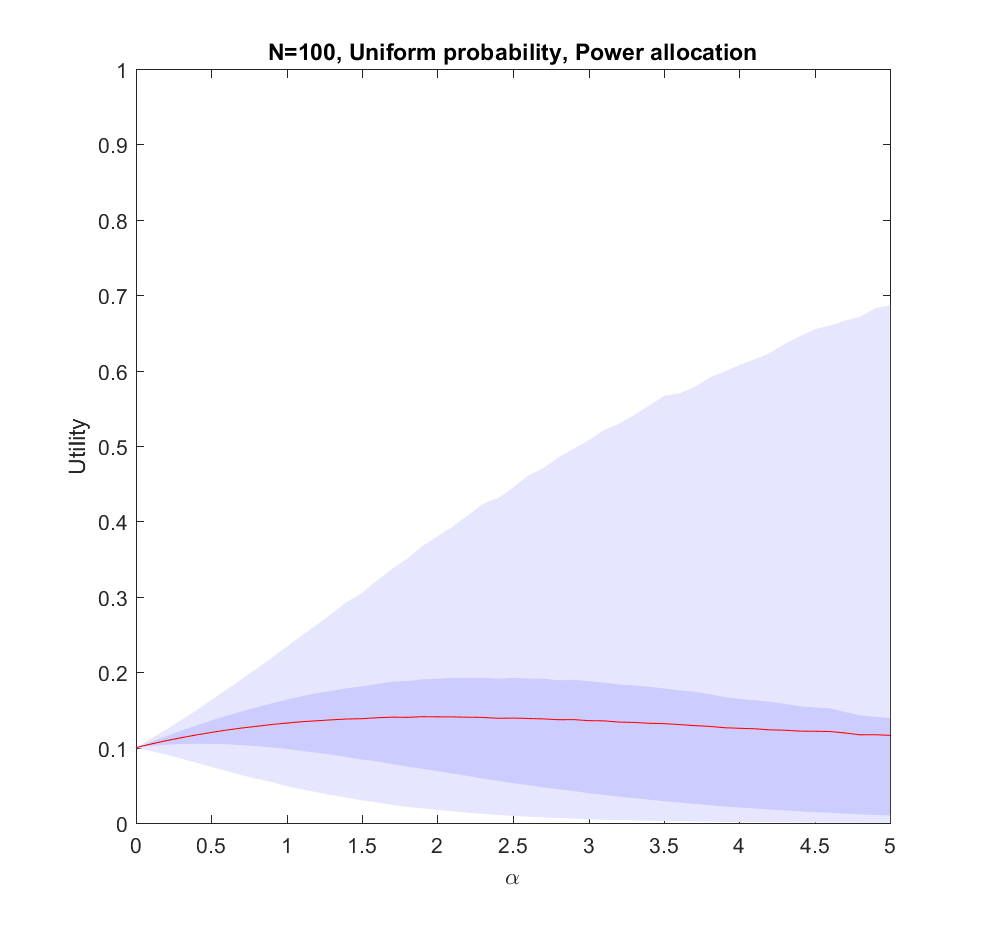
The $N=100$ case (where the probabilities are allocated based on a flat Dirichlet distribution) behaves similarly, but the expected utility is smaller since it is less likely that we will hit the right scenario.

What is going on?

This doesn’t seem to fit Robin’s or my intuitions at all! The best we can say about uniform allocation is that it doesn’t produce much regret: whatever happens, we will have made some allocation to the possibility. For large N this actually works out better than the directed allocation for a sizable fraction of realizations, but on average we get less utility than betting on the likely choices.

The problem with the model is of course that we actually know the probabilities before making the allocation. In reality, we do not know the likelihood of AI, WBE or alien invasions. We have some information, and we do have priors (like Robin’s view that $P_{AI} < 100 P_{WBE}$ ), but we are not able to allocate perfectly. A more plausible model would give us probability estimates instead of the actual probabilities.

We know nothing

Let us start by looking at the worst possible case: we do not know what the true probabilities are at all. We can draw estimates from the same distribution – it is just that they are uncorrelated with the true situation, so they are just noise.

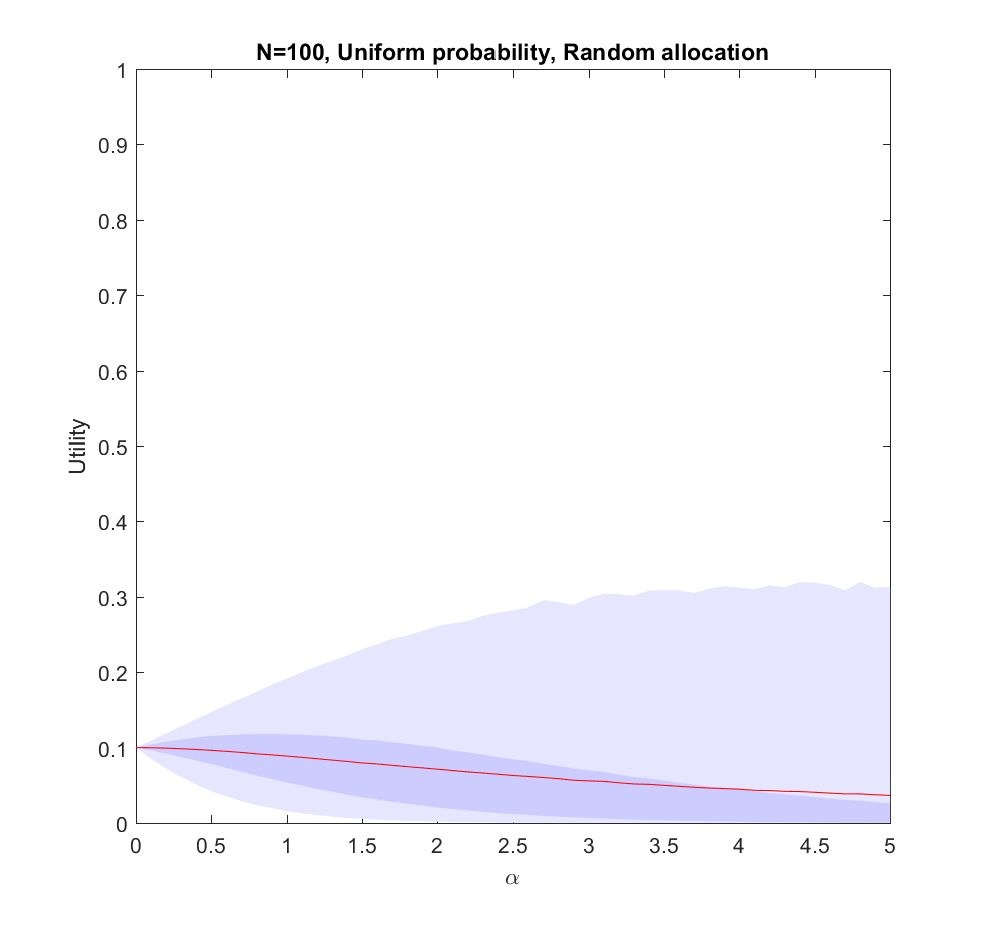
Utility of allocating effort as a power of the probability of scenarios, but the probabilities are just random guesses. Red line is expected utility, deeper blue envelope is lower and upper quartiles, lighter blue 95% interval. 100 possible scenarios, with uniform probability on the simplex.

In this case uniform distribution of effort is optimal. Not only does it avoid regret, it has a higher expected utility than trying to focus on a few scenarios ( $\alpha>0$ ). The larger N is, the less likely it is that we focus on the right scenario since we know nothing. The rationality of ignoring irrelevant information is pretty obvious.

Note that if we have to allocate a minimum effort to each investigated scenario we will be forced to effectively increase our $\alpha$ above 0. The above result gives the somewhat optimistic conclusion that the loss of utility compared to an even spread is rather mild: in the uniform case we have a pretty low amount of effort allocated to the winning scenario, so the low chance of being right in the nonuniform case is being balanced by having a slightly higher effort allocation on the selected scenarios. For high $\alpha$ there is a tail of rare big “wins” when we hit the right scenario that drags the expected utility upwards, even though in most realizations we bet on the wrong case. This is very much the hedgehog predictor story: ocasionally they have analysed the scenario that comes about in great detail and get intensely lauded, despite looking at the wrong things most of the time.

We know a bit

We can imagine that knowing more should allow us to gradually interpolate between the different results: the more you know, the more you should focus on the likely scenarios.

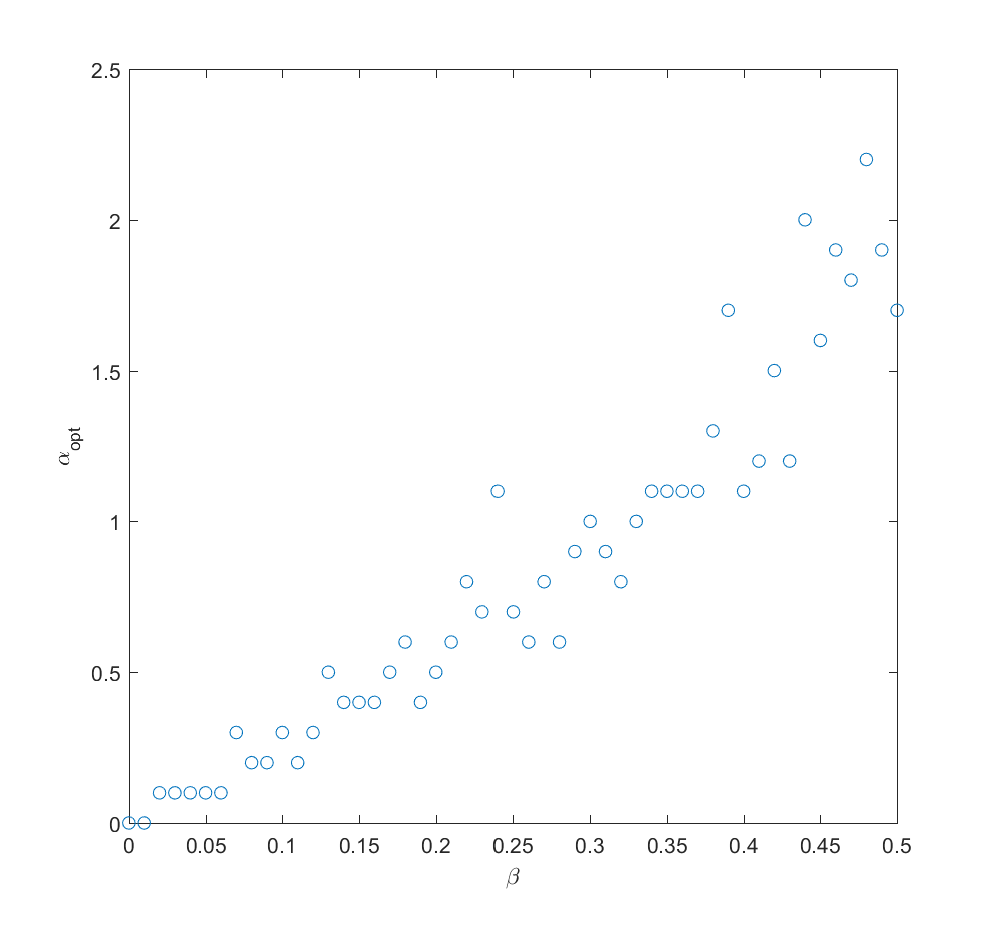
Optimal alpha as a function of how much information we have about the true probabilities. N=2. — Optimal alpha as a function of how much information we have about the true probabilities (noise due to Monte Carlo and discrete steps of alpha). N=2 (N=100 looks similar).

If we take the mean of the true probabilities with some randomly drawn probabilities (the “half random” case) the curve looks quite similar to the case where we actually know the probabilities: we get a maximum for $\alpha\approx 2$ . In fact, we can mix in just a bit ( $\beta$ ) of the true probability and get a fairly good guess where to allocate effort (i.e. we allocate effort as $a_i \propto (\beta P_i + (1-\beta)Q_i)^\alpha$ where $Q_i$ is uncorrelated noise probabilities). The optimal alpha grows roughly linearly with $\beta$ , $\alpha_{opt} \approx 4\beta$ in this case.

We learn

Adding a bit of realism, we can consider a learning process: after allocating some effort $\gamma$ to the different scenarios we get better information about the probabilities, and can now reallocate. A simple model may be that the standard deviation of noise behaves as $1/\sqrt{\tilde{a}_i}$ where $\tilde{a}_i$ is the effort placed in exploring the probability of scenario $i$ . So if we begin by allocating uniformly we will have noise at reallocation of the order of $1/\sqrt{\gamma/N}$ . We can set $\beta(\gamma)=\sqrt{\gamma/N}/C$ , where $C$ is some constant denoting how tough it is to get information. Putting this together with the above result we get $\alpha_{opt}(\gamma)=\sqrt{2\gamma/NC^2}$ . After this exploration, now we use the remaining $1-\gamma$ effort to work on the actual scenarios.

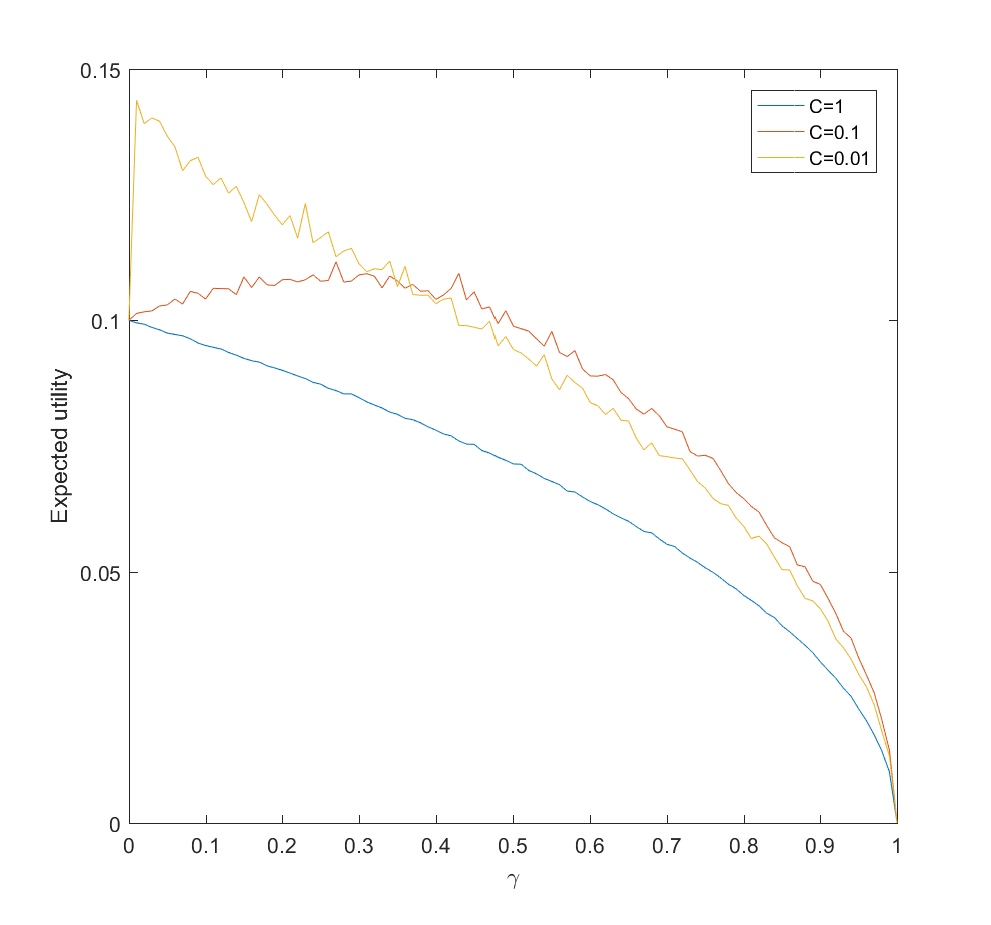
Expected utility as a function of amount of probability-estimating effort (gamma) for C=1 (hard to update probabilities), C=0.1 and C=0.01 (easy to update). N=100.

This is surprisingly inefficient. The reason is that the expected utility declines as $\sqrt{1-\gamma}$ and the gain is just the utility difference between the uniform case $\alpha=0$ and optimal $\alpha_{opt}$ , which we know is pretty small. If C is small (i.e. a small amount of effort is enough to figure out the scenario probabilities) there is an optimal nonzero $\gamma$ . This optimum $\gamma$ decreases as C becomes smaller. If C is large, then the best approach is just to spread efforts evenly.

Conclusions

So, how should we focus? These results suggest that the key issue is knowing how little we know compared to what can be known, and how much effort it would take to know significantly more.

If there is little more that can be discovered about what scenarios are likely, because our state of knowledge is pretty good, the world is very random, or improving knowledge about what will happen will be costly, then we should roll with it and distribute effort either among likely scenarios (when we know them) or spread efforts widely (when we are in ignorance).

If we can acquire significant information about the probabilities of scenarios, then we should do it – but not overdo it. If it is very easy to get information we need to just expend some modest effort and then use the rest to flesh out our scenarios. If it is doable but costly, then we may spend a fair bit of our budget on it. But if it is hard, it is better to go directly on the object level scenario analysis as above. We should not expect the improvement to be enormous.

Here I have used a square root diminishing return model. That drives some of the flatness of the optima: had I used a logarithm function things would have been even flatter, while if the returns diminish more mildly the gains of optimal effort allocation would have been more noticeable. Clearly, understanding the diminishing returns, number of alternatives, and cost of learning probabilities better matters for setting your strategy.

In the case of future studies we know the number of scenarios are very large. We know that the returns to forecasting efforts are strongly diminishing for most kinds of forecasts. We know that extra efforts in reducing uncertainty about scenario probabilities in e.g. climate models also have strongly diminishing returns. Together this suggests that Robin is right, and it is rational to stop clustering too hard on favorite scenarios. Insofar we learn something useful from considering scenarios we should explore as many as feasible.

Review of Robin Hanson’s The Age of Em

Introduction

Robin Hanson’s The Age of Em is bound to be a classic.

It might seem odd, given that it is both awkward to define what kind of book it is – economics textbook, future studies, speculative sociology, science fiction without any characters? – and that most readers will disagree with large parts of it. Indeed, one of the main reasons it will become classic is that there is so much to disagree with and those disagreements are bound to stimulate a crop of blogs, essays, papers and maybe other books.

This is a very rich synthesis of many ideas with a high density of fascinating arguments and claims per page just begging for deeper analysis and response. It is in many ways like an author’s first science fiction novel (Zindell’s Neverness, Rajaniemi’s The Quantum Thief, and Egan’s Quarantine come to mind) – lots of concepts and throwaway realizations has been built up in the background of the author’s mind and are now out to play. Later novels are often better written, but first novels have the freshest ideas.

The second reason it will become classic is that even if mainstream economics or futurism pass it by, it is going to profoundly change how science fiction treats the concept of mind uploading. Sure, the concept has been around for ages, but this is the first through treatment of what it means to a society. Any science fiction treatment henceforth will partially define itself by how it relates to the Age of Em scenario.

Plausibility

The Age of Em is all about the implications of a particular kind of software intelligence, one based on scanning human brains to produce intelligent software entities. I suspect much of the debate about the book will be more about the feasibility of brain emulations. To many people the whole concept sparks incredulity and outright rejection. The arguments against brain emulation range from pure arguments of incredulity (“don’t these people know how complex the brain is?”) over various more or less well-considered philosophical positions (“don’t these people read Heidegger?” to questioning the inherent functionalist reductionism of the concept) to arguments about technological feasibility. Given that the notion is one many people will find hard to swallow I think Robin spent too little effort bolstering the plausibility, making the book look a bit too much like what Nordmann called if-then ethics: assume some outrageous assumption, then work out the conclusion (which Nordmann finds a waste of intellectual resources). I think one can make fairly strong arguments for the plausibility, but Robin is more interested in working out the consequences. I have a feeling there is a need now for a good defense of the plausibility (this and this might be a weak start, but much more needs to be done).

Scenarios

In this book, I will set defining assumptions, collect many plausible arguments about the correlations we should expect from these assumptions, and then try to combine these many correlation clues into a self-consistent scenario describing relevant variables.

What I find more interesting is Robin’s approach to future studies. He is describing a self-consistent scenario. The aim is not to describe the most likely future of all, nor to push some particular trend the furthest it can go. Rather, he is trying to describe what, given some assumptions, is likely to occur based on our best knowledge and fits with the other parts of the scenario into an organic whole.

The baseline scenario I generate in this book is detailed and self-consistent, as scenarios should be. It is also often a likely baseline, in the sense that I pick the most likely option when such an option stands out clearly. However, when several options seem similarly likely, or when it is hard to say which is more likely, I tend instead to choose a “simple” option that seems easier to analyze.

This baseline scenario is a starting point for considering variations such as intervening events, policy options or alternatives, intended as the center of a cluster of similar scenarios. It typically is based on the status quo and consensus model: unless there is a compelling reason elsewhere in the scenario, things will behave like they have done historically or according to the mainstream models.

As he notes, this is different from normal scenario planning where scenarios are generated to cover much of the outcome space and tell stories of possible unfoldings of events that may give the reader a useful understanding of the process leading to the futures. He notes that the self-consistent scenario seems to be taboo among futurists.

Part of that I think is the realization that making one forecast will usually just ensure one is wrong. Scenario analysis aims at understanding the space of possibility better: hence they make several scenarios. But as critics of scenario analysis have stated, there is a risk of the conjunction fallacy coming into play: the more details you add to the story of a scenario the more compelling the story becomes, but the less likely the individual scenario. The scenario analyst respond by claiming individual scenarios should not be taken as separate things: they only make real sense as part of the bigger structure. The details are to draw the reader into the space of possibility, not to convince them that a particular scenario is the true one.

Robin’s maximal consistent scenario is not directly trying to map out an entire possibility space but rather to create a vivid prototype residing somewhere in the middle of it. But if it is not a forecast, and not a scenario planning exercise, what is it? Robin suggest it is a tool for thinking about useful action:

The chance that the exact particular scenario I describe in this book will actually happen just as I describe it is much less than one in a thousand. But scenarios that are similar to true scenarios, even if not exactly the same, can still be a relevant guide to action and inference. I expect my analysis to be relevant for a large cloud of different but similar scenarios. In particular, conditional on my key assumptions, I expect at least 30% of future situations to be usefully informed by my analysis. Unconditionally, I expect at least 10%.

To some degree this is all a rejection of how we usually think of the future in “far mode” as a neat utopia or dystopia with little detail. Forcing the reader into “near mode” changes the way we consider the realities of the scenario (compare to construal level theory). It makes responding to the scenario far more urgent than responding to a mere possibility. The closest example I know is Eric Drexler’s worked example of nanotechnology in Nanosystems and Engines of Creation.

Again, I expect much criticism quibbling about whether the status quo and mainstream positions actually fit Robin’s assumptions. I have a feeling there is much room for disagreement, and many elements presented as uncontroversial will be highly controversial – sometimes to people outside the relevant field, but quite often to people inside the field too (I am wondering about the generalizations about farmers and foragers). Much of this just means that the baseline scenario can be expanded or modified to include the altered positions, which could provide useful perturbation analysis.

It may be more useful to start from the baseline scenario and ask what the smallest changes are to the assumptions that radically changes the outcome (what would it take to make lives precious? What would it take to make change slow?) However, a good approach is likely to start by investigating robustness vis-à-vis plausible “parameter changes” and use that experience to get a sense of the overall robustness properties of the baseline scenario.

Beyond the Age of Em

But is this important? We could work out endlessly detailed scenarios of other possible futures: why this one? As Robin argued in his original paper, while it is hard to say anything about a world with de novo engineered artificial intelligence, the constraints of neuroscience and economics make this scenario somewhat more predictable: it is a gap in the mist clouds covering the future, even if it is a small one. But more importantly, the economic arguments seem fairly robust regardless of sociological details: copyable human/machine capital is economic plutonium (c.f. this and this paper). Since capital can almost directly be converted into labor, the economy will likely grow radically. This seems to be true regardless of whether we talk about ems or AI, and is clearly a big deal if we think things like the industrial revolution matter – especially a future disruption of our current order.

In fact, people have already criticized Robin for not going far enough. The age described may not last long in real-time before it evolves into something far more radical. As Scott Alexander pointed out in his review and subsequent post, an “ascended economy” where automation and on-demand software labor function together can be a far more powerful and terrifying force than merely a posthuman Malthusian world. It could produce some of the dystopian posthuman scenarios envisioned in Nick Bostrom’s “The future of human evolution“, essentially axiological existential threats where what gives humanity value disappears.

We do not yet have good tools for analyzing this kind of scenarios. Mainstream economics is busy with analyzing the economy we have, not future models. Given that the expertise to reason about the future of a domain is often fundamentally different from the expertise needed in the domain, we should not even assume economists or other social scientists to be able to say much useful about this except insofar they have found reliable universal rules that can be applied. As Robin likes to point out, there are far more results of that kind in the “soft sciences” than outsiders believe. But they might still not be enough to constrain the possibilities.

Yet it would be remiss not to try. The future is important: that is where we will spend the rest of our lives.

If the future matters more than the past, because we can influence it, why do we have far more historians than futurists? Many say that this is because we just can’t know the future. While we can project social trends, disruptive technologies will change those trends, and no one can say where that will take us. In this book, I’ve tried to prove that conventional wisdom wrong.

Andart II

Part of Anders' Exoself

robin hanson