Why do some musical tones sound consonant, and others dissonant? And how does this change with different musical instruments – or universes?
William Sethares has a great overview of this topic, from which I will borrow a lot (including his code). This thread was primed by this very good video, which got me thinking about a weird issue in theoretical music.
Pythagoras famously discovered that strings that had lengths in a rational ratio produces harmonious sounds. Galileo (1638) suggested that these sounds make the eardrum move regularly, and irregular motion sounds bad. Helmholtz (1863) suggested that tones with nearly similar frequencies produce a beating effect, which sounds dissonant. But he also noted that the overtones giving a sound its timbre also matters.
Plomp and Levelt (1965) measured people’s responses to mixes of two sine waves, which produced curves showing how pleasant and harmonious the mixes were. Several models have been built on top of their psychoacoustical work.
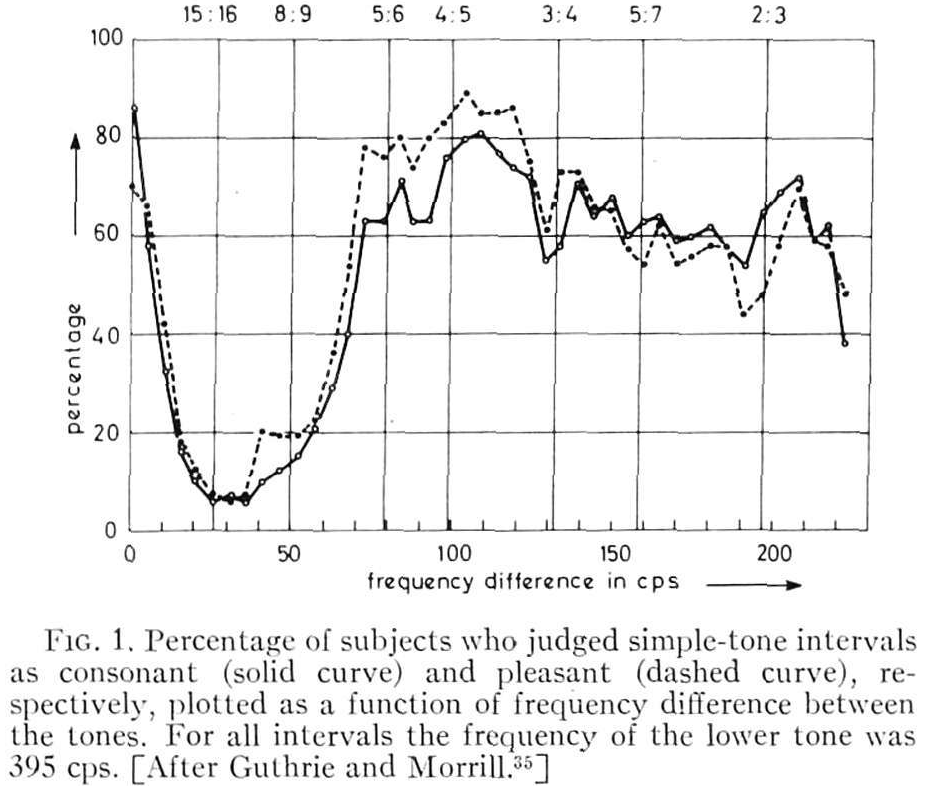
The assumed pattern is simple. Unison sounds great, near unison produces beats or (further away) roughness that sound bad, and gradually it turns into two separate simultaneous tones. A kind of uncanny valley.
Actual notes have overtones, and these also add to how much discordance you hear (Helmholtz). So if you play an instrument with overtones at 2, 3, 4, 5, … times the root frequency, two notes with different root frequencies will interact through all the combinations of overtones. Some may be consonant, others dissonant.
This can be calculated!
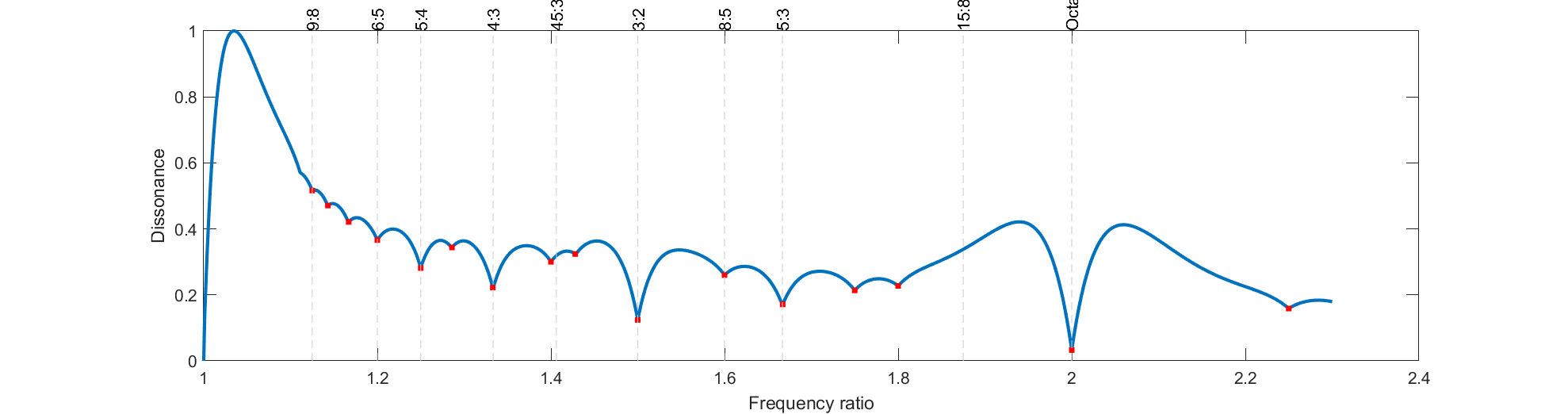
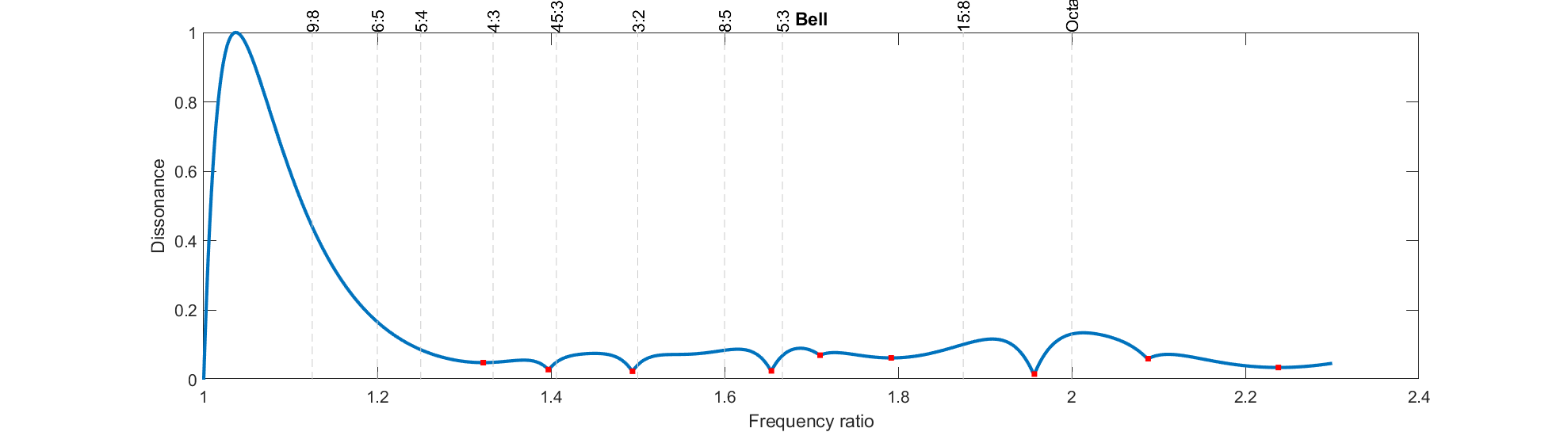
Doing this produces this cool plot. Note the dips (greater harmony) at certain frequencies: this is where all the overtones align. These dips at rational points correspond to the just interval scale.
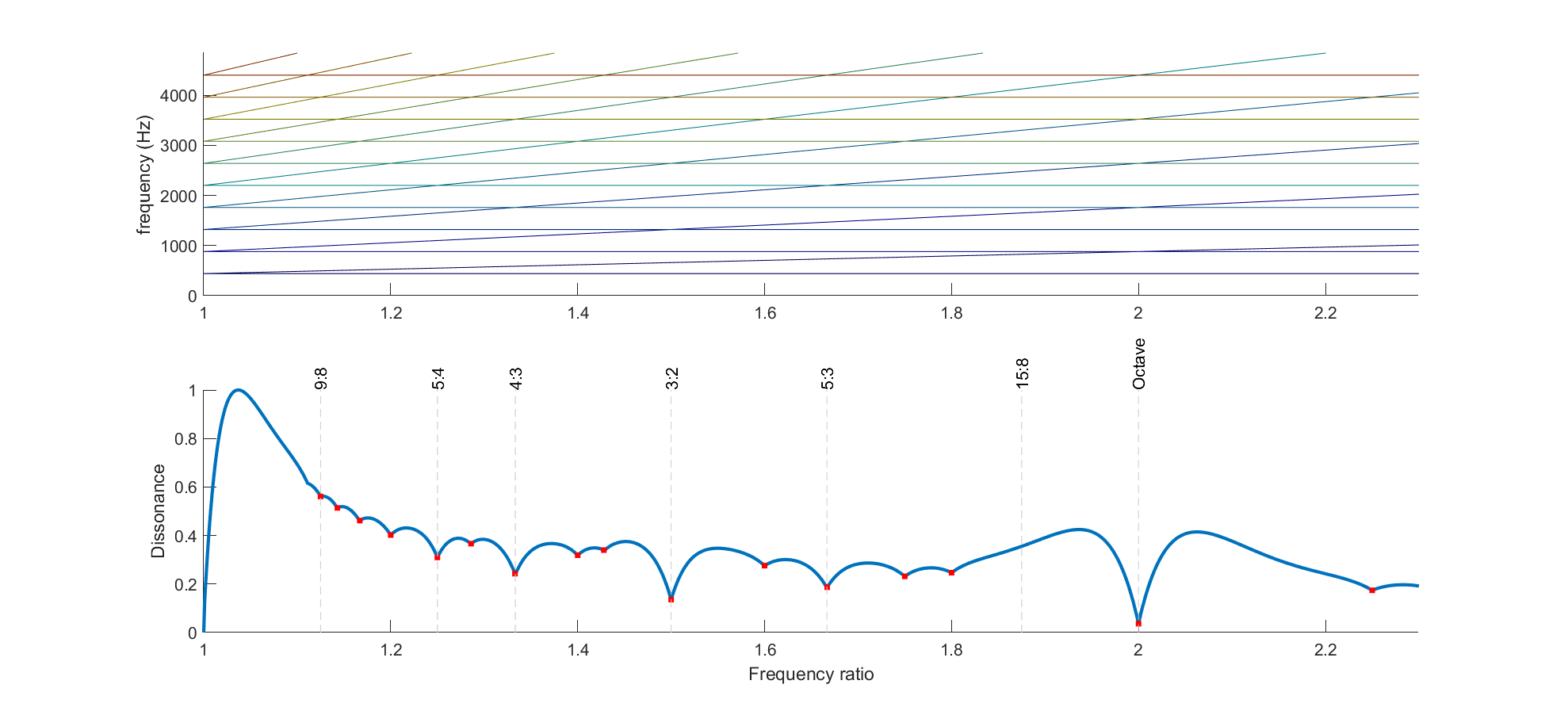
You can see why the dips occur if we plot the spectrum above the curve. The lines denote the frequencies of the root and overtones of the two tones played: when there are multiple crossings there is more harmony. These correspond in this case to the rational ratios of the root frequencies: not a coincidence!
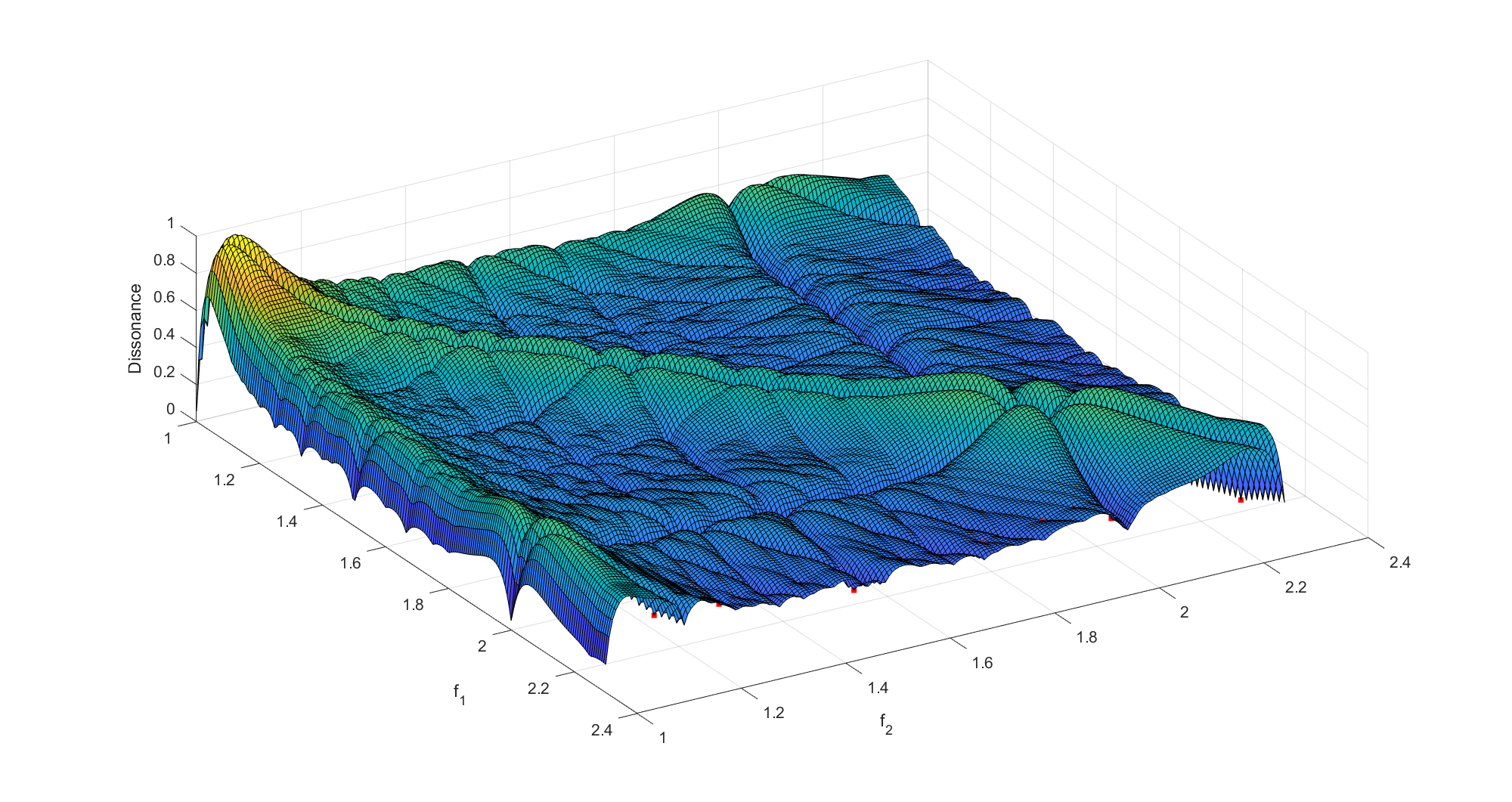
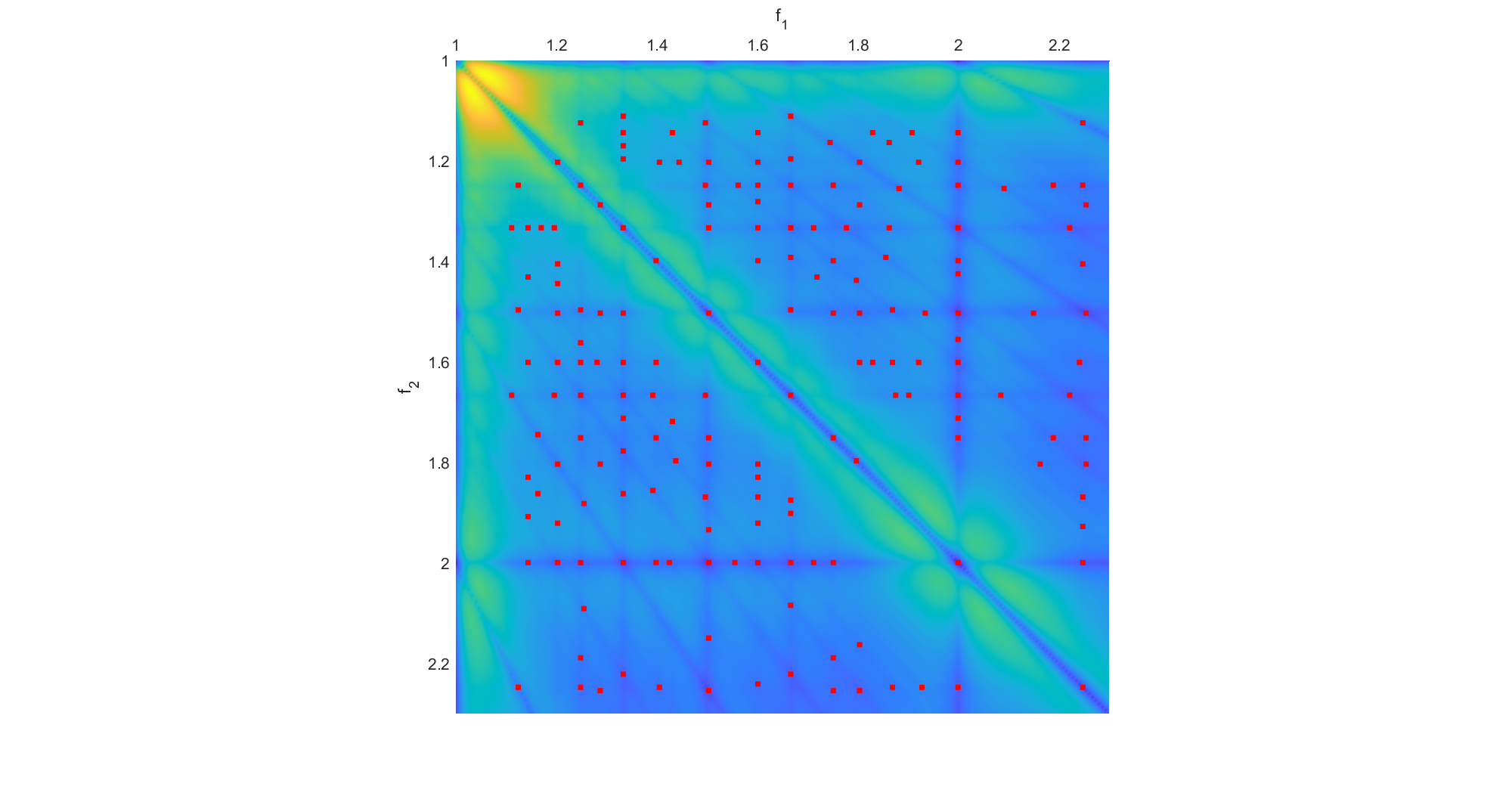
You can also do a 2D plot of the interactions between the notes in a triad.
Plotting the local minima suggests triads that ought to sound good. I have no doubt most of them have established names (I have serious trouble interpreting music-speak). One can also consider chords with four tones, although the visualization becomes more complex.
Universal harmony from math, right?
Hah! In the above plots I assumed that the overtones had frequencies that were integer multiples of the root. This is true for
strings and
pipe instruments.
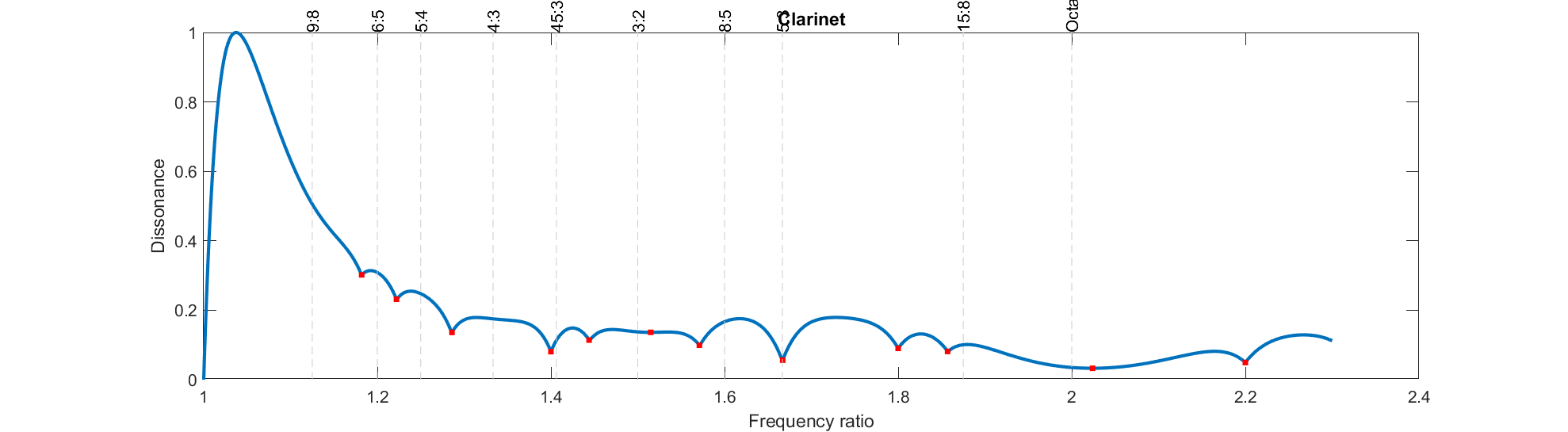
Clarinets only have odd harmonics. Bells,
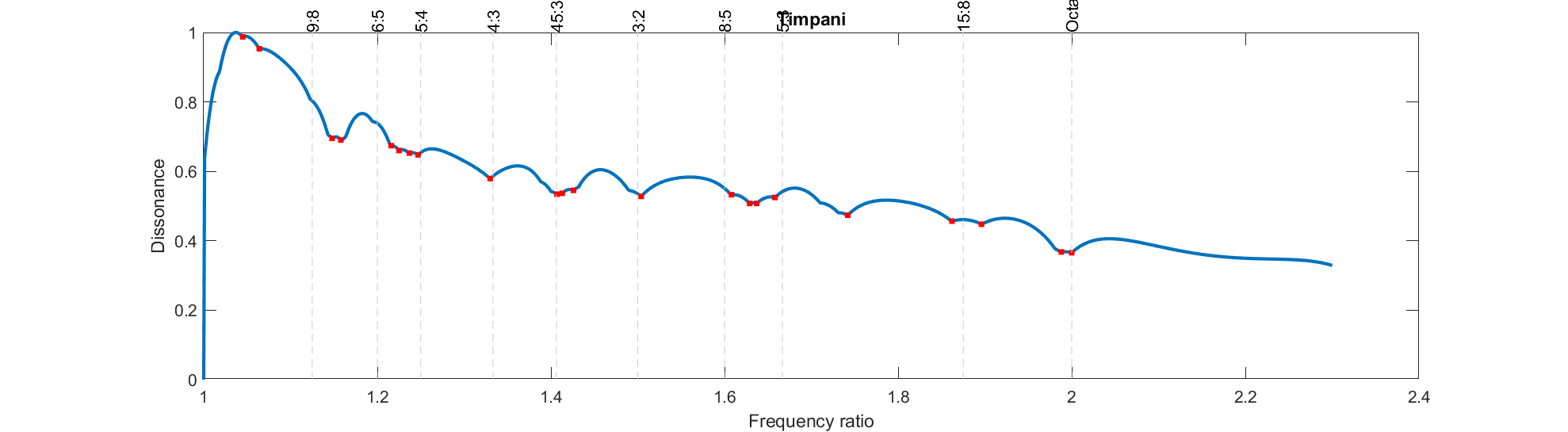
timpani and
bars have different spectrums. These things affect the timbre, how the instrument sounds. But these changes will also change the dissonance curve – making the previous consonance locations change. They no longer correspond to the standard tunings!
So much for the perfect harmony of the spheres!
Bells and gamelans don’t lend themselves to the standard scales (Gamelan also has rather few pitches, which means meshing it with Western scales is troublesome. This produced some of the really memorable parts of the music of Akira soundtrack by Shoji Yamashiro; see
this really interesting video analysis of how Kaneda’s and Tesuo’s themes got their character from this.). One can tune bells or bars to fit with a given scale with some effort. In many cultures commonly used instruments have timbres that make different scales sound better. One can also (
Sethares is interested in this) take some weird synthesized timbre and figure out scales that work with it.
I also assumed amplitudes declining like 1/n (ideal struck or bowed strings, wind instruments). Plucking goes as 1/n^2, and plucking very near the bridge excites all harmonics strongly (bright sound). The more overtones, the messier the dissonance diagram. But the basic structure remains.
Why I looked into this: I was dusting off an old project about music in universes with extra time dimensions, and wondered if harmony worked entirely differently there. To my delight it looks like the basic scheme is independent of number of time dimensions! Hearing in such universes presumably involves an ear that vibrates like a string or surface, allowing standard separation of variables of the different time dimensions. You get separate consonance for the different dimensions, and demanding notes of the same fundamental pitch to be in harmony forces a
Pythagorean triple relation, which produces some very strange scales.
The cool thing about this entire scheme is that the pattern does come from the mathematics of eigenvalues of differential equations. It is not arbitrary. In a sense it is universal to creatures that do not like stimuli that cannot be well separated.
But it should not be assumed to be the full truth. The psychoacoustic assumptions here are only typical: there are plenty of individual variation. Cultural tastes and training differ. Perhaps most importantly, one should not assume harmony is the end-all of music. Music is sound and silence distributed over time, not necessarily harmonious sounds.