Quantifying busyness

Tempus fugit

If I have one piece of advice to give to people, it is that they typically have way more time now than they will ever have in the future. Do not procrastinate, take chances when you see them – you might never have the time to do it later.

One reason is the gradual speeding up of subjective time as we age: one day is less time for a 40 year old than for a 20 year old, and way less than the eon it is to a 5 year old. Another is that there is a finite risk that opportunities will go away (including our own finite lifespans). The main reason is of course the planning fallacy: since we underestimate how long our tasks will take, our lives tend to crowd up. Accepting to give a paper in several months time is easy, since there seems to be a lot of time to do it in between… which mysteriously disappears until you sit there doing an all-nighter. There is also the likely effect that as you grow in skill, reputation and career there will be more demands on your time. All in all, expect your time to grow in preciousness!

Mining my calendar

I recently noted that my calendar had filled up several weeks in advance, something I think did not happen to this extent a few years back. A sign of a career taking off, worsening time management, or just bad memory? I decided to do some self-quantification using my Google calendar. I exported the calendar as an .ics file and made a simple parser in Matlab.

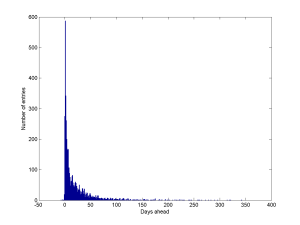
Histogram of time distance between scheduling time and actual event.

It is pretty clear from a scatter plot that most entries are for the near future – a few days or weeks ahead. Looking at a histogram shows that most are within a month (a few are in the past – I sometimes use my calendar to note when I have done something like an interview that I may want to remember later).

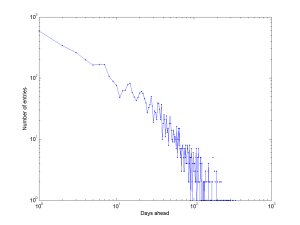
Log-log plot of the histogram of event scheduling intervals.

Plotting it as a log-log diagram suggests it is lighter-tailed than a power-law: there is a characteristic scale. And there are a few wobbles suggesting 1-week, 2-week and 3-week periodicities.

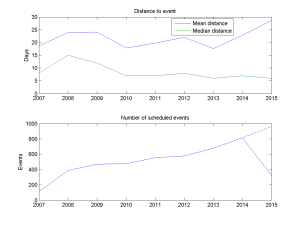
Mean and median distance to newly scheduled events (top), annual number of events scheduled (bottom). The eventual 2015 annual number has been estimated (dashed line).

Am I getting busier? Plotting the mean and median distance to scheduled events, and the number of events per year, suggests yes. The median distance to the things I schedule seems to be creeping downwards, while the number of events per year has clearly doubled from about 400 in 2008 to 800 in 2014 (and extrapolating 2015 suggests about 1000 scheduled events).

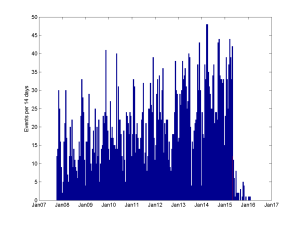
Number of calendar events per 14 day period. Red line marks present.

Plotting the number of events I had per 14-day period also suggests that I have way more going on now than a few years ago. The peaks are getting higher and the mean period is more intense.

When am I free?

A good measure of busyness would be the time horizon: how far ahead should you ask me for a meeting if you want to have a high chance of getting it?

One approach would be to look for the probability $Q(t)$ that a day $t$ days ahead is entirely empty. If the probability that I will fill in something $i$ days ahead is $P(i)$ , then the chance for an empty day is $Q(t) = \prod_{i=t}^\infty (1-P(i))$ . We can estimate $P(i)$ by doing a curve-fit (a second degree curve works well), but we can of course just estimate from the histogram counts: $\hat{P}(i)=N(i)/N$ .

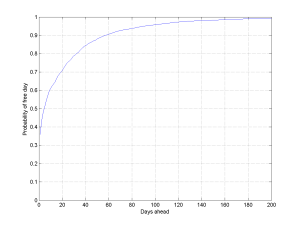
Probability that I will have an entirely free day a certain number of days ahead.

However, this method is slightly wrong. Some days are free, others have many different events. If I schedule twice as many events the chance of a free day should be lower. A better way of estimating $Q(t)$ is to think in terms of the rate of scheduling. We can view this as a Poisson process, where the rate of scheduling $\lambda(i)$ tells us how often I schedule something $i$ days ahead. An approximation is $\hat{\lambda}(i)=N(i)/T$ , where $T$ is the time interval we base our estimate on. This way $Q(t) = \prod_{i=t}^\infty e^{-\lambda(i)}$ .

Probability that I will be free a certain number of days ahead for different years of my calender, estimated using a Poisson rate model.

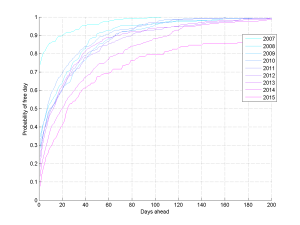
If we slice the data by year, then there seems to be a fairly clear trend towards the planning horizon growing – I have more and more events far into future, and I have more to do. Oh, those halcyon days in 2007 when I presumably just lazed around…

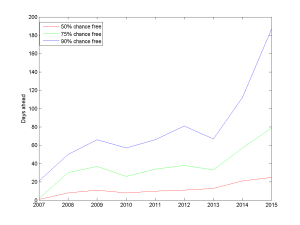
Distance to first day where I have 50%, 75% or 90% chance of being entirely unscheduled.

If we plot when I have 50%, 75% and 90% chance of being free, the trend is even clearer. At present you need to ask about three weeks in advance to have a 50% chance of grabbing me, and 187 days in advance to be 90% certain (if you want an entire working week with 50% chance, this is close to where you should go). Back in 2008 the 50% point was about a week and the 90% point 1.5 months ahead. I have become around 3 times busier.

Conclusions

So, I have become busier. This is of course no evidence of getting more done – a lot of events are pointless meetings, and who knows if I am doing anything helpful at the other events. Plus, I might actually be wasting my time doing statistics and blogging instead of working.

But the exercise shows that it is possible to automatically estimate necessary planning horizons. Maybe we should add this to calendar apps to help scheduling: my contact page or virtual secretary might give you an automatically updated estimate of how far ahead you need to schedule things to have a good chance of getting me. It doesn’t have to tell you my detailed schedule (in principle one could do a privacy attack on the schedule by asking for very specific dates and seeing if they were blocked).

We can also use this method to look at levels of busyness across organisations. Who have flexibility in their schedules, who are so overloaded that they cannot be effectively involved in projects? In the past, tasks tended to be simple and the issue was just the amount of time people had. But today we work individually yet as part of teams, and coordination (meetings, seminars, lectures) are the key links: figuring out how to schedule them right is important for effectivity.

If team member $j$ has scheduling rates $\lambda_j(i)$ and they are are uncorrelated (yeah, right), then $Q(t)=\prod_{i=t}^\infty e^{-\sum_j\lambda_j(i)}$ . The most important lesson is that the chance of everybody being able to make it to any given meeting day declines exponentially with the number of people. If the $\lambda_j(i)$ decline exponentially with time (plausible in at least my case) then scheduling a meeting requires the time ahead to be proportional to the number of people involved: double the meeting size, at least double the planning horizon. So if you want nimble meetings, make them tiny.

In the end, I prefer to live by the advice my German teacher Ulla Landvik once gave me, glancing at the school clock: “I see we have 30 seconds left of the lesson. Let’s do this excercise – we have plenty of time!” Time not only flies, it can be stretched too.

Addendum 2015-05-01

Some further explorations.

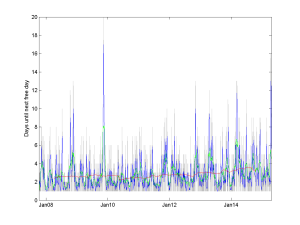
Days until next completely free day as a function of time. Grey shows data day-by-day, blue averaged over 7 days, green 30 days and red one year.

Owen Cotton-Barratt pointed out that another measure of busyness might be the distance to the next free day. Plotting it shows a very bursty pattern, with noisy peaks. The mean time was about 2-3 days: even though a lot of time the horizon is far away, often an empty day slips through too. It is just that it cannot be relied on.

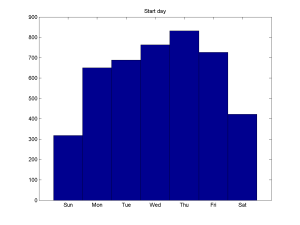
Histogram of the timing of events by weekday.

Are there periodicities? The most obvious is the weekly dynamics: Thursdays are busiest, weekend least busy. I tend to do scheduling in a roughly similar manner, with Tuesdays as the top scheduling day.

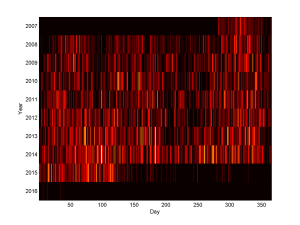
Number of events scheduled per day, plotted across my calendar.

Over the years, plotting the number of events per day (“event intensity”) it is also clear that there is a loose pattern. Back in 2008-2011 one can see a lower rate around day 75 – that is the break between Hilary and Trinity term here in Oxford. There is another trough around day 200-250, the summer break and the time before the Michaelmas term. However, this is getting filled up over time.

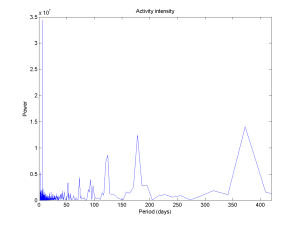
Periodogram of event intensity, showing periodicities in my schedule. Note the weekly and yearly peaks.

Making a periodogram produces an obvious peak for 7 days, and a loose yearly periodicity. Between them there is a bunch of harmonics. The funny thing is that the week periodicity is very strong but hard to see in the map above.

Crispy embryos

Researchers at Sun Yat-sen University in Guangzhou have edited the germline genome of human embryos (paper). They used the ever more popular CRISPR/Cas9 method to try to modify the gene involved in beta-thalassaemia in non-viable leftover embryos from a fertility clinic.

As usual there is a fair bit of handwringing, especially since there was a recent call for a moratorium on this kind of thing from one set of researchers, and a more liberal (yet cautious) response from another set. As noted by ethicists, many of the ethical concerns are actually somewhat confused.

That germline engineering can have unpredictable consequences for future generations is as true for normal reproduction. More strongly, somebody making the case that (say) race mixing should be hindred because of unknown future effects would be condemned as a racist: we have overarching reasons to allow people live and procreate freely that morally overrule worries about their genetic endowment – even if there actually were genetic issues (as far as I know all branches of the human family are equally interfertile, but this might just be a historical contingency). For a possible future effect to matter morally it needs to be pretty serious and we need to have some real reason to think it is more likely to happen because of the actions we take now. A vague unease or a mere possibility is not enough.

However, the paper actually gives a pretty good argument for why we should not try this method in humans. They found that the efficiency of the repair was about 50%, but more worryingly that there was off-target mutations and that a similar gene was accidentally modified. These are good reasons not to try it. Not unexpected, but very helpful in that we can actually make informed decisions both about whether to use it (clearly not until the problems have been fixed) and what needs to be investigated (how can it be done well? why does it work worse here than advertised?).

The interesting thing with the paper is that the fairly negative results which would reduce interest in human germline changes is anyway hailed as being unethical. It is hard to make this claim stick, unless one buys into the view that germline changes of human embryos is intrinsically bad. The embryos could not develop into persons and would have been discarded from the fertility clinic, so there was no possible future person being harmed (if one thinks fertilized but non-viable embryos deserve moral protection one has other big problems). The main fear seems to be that if the technology is demonstrated many others will follow, but an early negative result would seem to reduce this slippery slope argument.

I think the real reason people think there is an ethical problem is the association of germline engineering with “designer babies”, and the conditioning that designer babies are wrong. But they can’t be wrong for no reason: there has to be an ethics argument for their badness. There is no shortage of such arguments in the literature, ranging from ideas of the natural order, human dignity, accepting the given, the importance of an open-ended life to issues of equality, just to mention a few. But none of these are widely accepted as slam-dunk arguments that conclusively show designer babies are wrong: each of them also have vigorous criticisms. One can believe one or more of them to be true, but it would be rather premature to claim that settles the debate. And even then, most of these designer baby arguments are irrelevant for the case at hand.

All in all, it was a useful result that probably will reduce both risky and pointless research and focus on what matters. I think that makes it quite ethical.

The end of the worlds

George Dvorsky has a piece on Io9 about ways we could wreck the solar system, where he cites me in a few places. This is mostly for fun, but I think it links to an important existential risk issue: what conceivable threats have big enough spatial reach to threaten a interplanetary or even star-faring civilization?

This matters, since most existential risks we worry about today (like nuclear war, bioweapons, global ecological/societal crashes) only affect one planet. But if existential risk is the answer to the Fermi question, then the peril has to strike reliably. If it is one of the local ones it has to strike early: a multi-planet civilization is largely immune to the local risks. It will not just be distributed, but it will almost by necessity have fairly self-sufficient habitats that could act as seeds for a new civilization if they survive. Since it is entirely conceivable that we could have invented rockets and spaceflight long before discovering anything odd about uranium or how genetics work it seems unlikely that any of these local risks are “it”. That means that the risks have to be spatially bigger (or, of course, that xrisk is not the answer to the Fermi question).

Of the risks mentioned by George physics disasters are intriguing, since they might irradiate solar systems efficiently. But the reliability of them being triggered before interstellar spread seems problematic. Stellar engineering, stellification and orbit manipulation may be issues, but they hardly happen early – lots of time to escape. Warp drives and wormholes are also likely late activities, and do not seem to be reliable as extinctors. These are all still relatively localized: while able to irradiate a largish volume, they are not fine-tuned to cause damage and does not follow fleeing people. Dangers from self-replicating or self-improving machines seems to be a plausible, spatially unbound risk that could pursue (but also problematic for the Fermi question since now the machines are the aliens). Attracting malevolent aliens may actually be a relevant risk: assuming von Neumann probes one can set up global warning systems or “police probes” that maintain whatever rules the original programmers desire, and it is not too hard to imagine ruthless or uncaring systems that could enforce the great silence. Since early civilizations have the chance to spread to enormous volumes given a certain level of technology, this might matter more than one might a priori believe.

So, in the end, it seems that anything releasing a dangerous energy effect will only affect a fixed volume. If it has energy $E$ and one can survive it below a deposited energy $e$ , if it just radiates in all directions the safe range is $r = \sqrt{E/4 \pi e} \propto \sqrt{E}$ – one needs to get into supernova ranges to sterilize interstellar volumes. If it is directional the range goes up, but smaller volumes are affected: if a fraction $f$ of the sky is affected, the range increases as $\propto \sqrt{1/f}$ but the total volume affected scales as $\propto f\sqrt{1/f}=\sqrt{f}$ .

Self-sustaining effects are worse, but they need to cross space: if their space range is smaller than interplanetary distances they may destroy a planet but not anything more. For example, a black hole merely absorbs a planet or star (releasing a nasty energy blast) but does not continue sucking up stuff. Vacuum decay on the other hand has indefinite range in space and moves at lightspeed. Accidental self-replication is unlikely to be spaceworthy unless is starts among space-moving machinery; here deliberate design is a more serious problem.

The speed of threat spread also matters. If it is fast enough no escape is possible. However, many of the replicating threats will have sublight speed and could hence be escaped by sufficiently paranoid aliens. The issue here is if lightweight and hence faster replicators can always outrun larger aliens; given the accelerating expansion of the universe it might be possible to outrun them by being early enough, but our calculations do suggest that the margins look very slim.

The more information you have about a target, the better you can in general harm it. If you have no information, merely randomizing it with enough energy/entropy is the only option (and if you have no information of where it is, you need to radiate in all directions). As you learn more, you can focus resources to make more harm per unit expended, up to the extreme limits of solving the optimization problem of finding the informational/environmental inputs that cause desired harm (=hacking). This suggests that mindless threats will nearly always have shorter range and smaller harms than threats designed by (or constituted by) intelligent minds.

In the end, the most likely type of actual civilization-ending threat for an interplanetary civilization looks like it needs to be self-replicating/self-sustaining, able to spread through space, and have at least a tropism towards escaping entities. The smarter, the more effective it can be. This includes both nasty AI and replicators, but also predecessor civilizations that have infrastructure in place. Civilizations cannot be expected to reliably do foolish things with planetary orbits or risky physics.

[Addendum: Charles Stross has written an interesting essay on the risk of griefers as a threat explanation. ]

[Addendum II: Robin Hanson has a response to the rest of us, where he outlines another nasty scenario. ]

Do we want the enhanced military?

Some notes on Practical Ethics inspired by Jonathan D. Moreno’s excellent recent talk.

My basic argument is that enhancing the capabilities of military forces (or any other form of state power) is risky if the probability that they can be misused (or the amount of expected/maximal damage in such cases) does not decrease more strongly. This would likely correspond to some form of moral enhancement, but even the morally enhanced army may act in a bad manner because the values guiding it or the state commanding it are bad: moral enhancement as we normally think about it is all about coordination, the ability to act according to given values and to reflect on these values. But since moral enhancement itself is agnostic about the right values those values will be provided by the state or society. So we need to ensure that states/societies have good values, and that they are able to make their forces implement them. A malicious or stupid head commanding a genius army is truly dangerous. As is tails wagging dogs, or keeping the head unaware (in the name of national security) of what is going on.

In other news: an eclipse in a teacup:

Consequentialist world improvement

I just rediscovered an old response to the Extropians List that might be worth reposting. Slight edits.

On 06/10/2012 16:17, Tomaz Kristan wrote:

>> If you want to reduce death tolls, focus on self-driving cars.
> Instead of answering terror attacks, just mend you cars?

Sounds eminently sensible. Charlie makes a good point: if we want to make the world better, it might be worth prioritizing fixing the stuff that makes it worse according to the damage it actually makes. Toby Ord and me have been chatting quite a bit about this.

Death

In terms of death (~57 million people per year), the big causes are cardiovascular disease (29%), infectious and parasitic diseases (23%) and cancer (12%). At least the first and last are to a sizeable degree caused or worsened by ageing, which is a massive hidden problem. It has been argued that malnutrition is similarly indirectly involved in 15-60% of the total number of deaths: often not the direct cause, but weakening people so they become vulnerable to other risks. Anything that makes a dent in these saves lives on a scale that is simply staggering; any threat to our ability to treat them (like resistance to antibiotics or anthelmintics) is correspondingly bad.

Unintentional injuries are responsible for 6% of deaths, just behind respiratory diseases 6.5%. Road traffic alone is responsible for 2% of all deaths: even 1% safer cars would save 11,400 lives per year. If everybody reached Swedish safety (2.9 deaths per 100,000 people per year) it would save around 460,000 lives per year – one Antwerp per year.

Now, intentional injuries are responsible for 2.8% of all deaths. Of these suicide is responsible for 1.53% of total death rate, violence 0.98% and war 0.3%. Yes, all wars killed about the same number of people as were killed by meningitis, and slightly more than the people who died of syphilis. In terms of absolute numbers we might be much better off improving antibiotic treatments and suicide hotlines than trying to stop the wars. And terrorism is so small that it doesn’t really show up: even the highest estimates put the median fatalities per year in the low thousands.

So in terms of deaths, fixing (or even denting) ageing, malnutrition, infectious diseases and lifestyle causes is a far more important activity than winning wars or stopping terrorists. Hypertension, tobacco, STDs, alcohol, indoor air pollution and sanitation are all far, far more pressing in terms of saving lives. If we had a choice between ending all wars in the world and fixing indoor air pollution the rational choice would be to fix those smoky stoves: they kill nine times more people.

Existential risk

There is of course more to improving the world than just saving lives. First there is the issue of outbreak distributions: most wars are local and small affairs, but some become global. Same thing for pandemic respiratory disease. We actually do need to worry about them more than their median sizes suggest (and again the influenza totally dominates all wars). Incidentally, the exponent for the power law distribution of terrorism is safely strongly negative at -2.5, so it is less of a problem than ordinary wars with exponent -1.41 (where the expectation diverges: wait long enough and you get a war larger than any stated size).

There are reasons to think that existential risk should be weighed extremely strongly: even a tiny risk that we loose all our future is much worse than many standard risks (since the future could be inconceivably grand and involve very large numbers of people). This has convinced me that fixing the safety of governments needs to be boosted a lot: democides have been larger killers than wars in the 20th century and both seems to have most of the tail risk, especially when you start thinking nukes. It is likely a far more pressing problem than climate change, and quite possibly (depending on how you analyse xrisk weighting) beats disease.

How to analyse xrisk, especially future risks, in this kind of framework is a big part of our ongoing research at FHI.

Happiness

If instead of lives lost we look at the impact on human stress and happiness wars (and violence in general) look worse: they traumatize people, and terrorism by its nature is all about causing terror. But again, they happen to a small set of people. So in terms of happiness it might be more important to make the bulk of people happier. Life satisfaction correlates to 0.7 with health and 0.6 with wealth and basic education. Boost those a bit, and it outweighs the horrors of war.

In fact, when looking at the value of better lives, it looks like an enhancement in life quality might be worth much more than fixing a lot of the deaths discussed above: make everybody’s life 1% better, and it corresponds to more quality adjusted life years than is lost to death every year! So improving our wellbeing might actually matter far, far more than many diseases. Maybe we ought to spend more resources on applied hedonism research than trying to cure Alzheimers.

Morality

The real reason people focus so much about terrorism is of course the moral outrage. Somebody is responsible, people are angry and want revenge. Same thing for wars. And the horror tends to strike certain people: my kind of global calculations might make sense on the global scale, but most of us think that the people suffering the worst have a higher priority. While it might make more utilitarian sense to make everybody 1% happier rather than stop the carnage in Syria, I suspect most people would say morality is on the other side (exactly why is a matter of some interesting ethical debate, of course). Deontologists might think we have moral duties we must implement no matter what the cost. I disagree: burning villages in order to save them doesn’t make sense. It makes sense to risk lives in order to save lives, both directly and indirectly (by reducing future conflicts).

But this requires proportionality: going to war in order to avenge X deaths by causing 10X deaths is not going to be sustainable or moral. The total moral weight of one unjust death might be high, but it is finite. Given the typical civilian causality ratio of 10:1 any war will also almost certainly produce far more collateral unjust deaths than the justified deaths of enemy soldiers: avenging X deaths by killing exactly X enemies will still lead to around 10X unjust deaths. So achieving proportionality is very, very hard (and the Just War Doctrine is broken anyway, according to the war ethicists I talk to). This means that if you want to leave the straightforward utilitarian approach and add some moral/outrage weighting, you risk making the problem far worse by your own account. In many cases it might indeed be the moral thing to turn the other cheek… ideally armoured and barbed with suitable sanctions.

Conclusion

To sum up, this approach of just looking at consequences and ignoring who is who is of course a bit too cold for most people. Most people have Tetlockian sacred values and get very riled up if somebody thinks about cost-effectiveness in terrorism fighting (typical US bugaboo) or development (typical warmhearted donor bugaboo) or healthcare (typical European bugaboo). But if we did, we would make the world a far better place.

Bring on the robot cars and happiness pills!

Future Humans: science fiction and human enhancement

Recording of a fun panel we (Imre Bard, Caroline Edwards, Adam Roberts and me) had at the LSE 2015 literary festival about science fiction, human enhancement and cyborgs. Are cyborgs neoliberal, and what about collectivist libertarian solutions like information markets?

Continued integrals

Many of the most awesome formulas you meet when getting into mathematics are continued fractions like

$\Phi = 1+\frac{1}{1+\frac{1}{1+\frac{1}{\ldots}}}$

and nested radicals like

$2 = \sqrt{2 + \sqrt{2 + \sqrt{2 + \ldots}}}$ .

What about nested/continued integrals? Here is a simple one:

$e^x=1+x+\int x+\left(\int x+\left(\int x+\left(\ldots\right)dx\right)dx\right)dx$ .

The way to see this is to recognize that the x in the first integral is going to integrate to $x^2/2$ , the x in the second will be integrated twice $\int x^2/2 dx = x^3/3!$ , and so on.

In general additive integrals of this kind turn into sums (assuming convergence, handwave, handwave…):

$I(x)=\int f(x)+\left(\int f(x)+\left(\int f(x)+\left(\ldots\right)dx\right)dx\right)dx = \sum_{n=1}^\infty \int^n f(x) dx$ .

On the other hand, $I'(x)=f(x)+I(x)$ .

So if we insert $f_k(x)=\sin(kx)$ we get the sum $I_k(x)=-\cos(kx)/k-\sin(kx)/k^2+\cos(kx)/k^3+\sin(x)/k^4-\cos(kx)/k^5-\ldots$ . For $x=0$ we end up with $I_k(0)=\sum_{n=0}^\infty 1/k^{4n+2} - \sum_{n=0}^\infty 2/k^{4n+1}$ . The differential equation has solution $I_k(x)=ce^x-\sin(kx)/(k^2+1) - k\cos(kx)/(k^2+1)$ . Setting $k=0$ the integral is clearly zero, so $c=0$ . Tying it together we get:

$\sum_{n=0}^\infty 1/k^{4n+2}-\sum_{n=0}^\infty 1/k^{4n+1}=-k/(k^2+1)$ .

Things are trickier when the integrals are multiplicative, like $I(x)=\int x \int x \int x \ldots dx dx dx$ . However, we can turn it into a differential equation: $I'(x)=x I(x)$ which has the well known solution $I(x)=ce^{x^2/2}$ . Same thing for $f_k(x)=\sin(kx)$ , giving us $I_k(x)=ce^{-\cos(kx)/k}$ . Since we are running indefinite integrals we get those pesky constants.

Plugging in $f(x)=1/x$ gives $I(x)=cx$ . If we set $c=1$ we get the mildly amusing and in retrospect obvious formula

$x=\int \frac{\int \frac{\int \frac{\ldots}{x} dx}{x} dx}{x} dx$ .

We can of course mess things up further, like $I(x)=\int\sqrt{\int\sqrt{\int\sqrt{\ldots} dx} dx} dx$ , where the differential equation becomes $I'^2=I$ with the solution $I(x)=(1/4)(c^2 + 2cx + x^2)$ . A surprisingly simple solution to a weird-looking integral. In a similar vein:

$2\cot^{-1}(e^{c-x})=\int\sin\left(\int\sin\left(\int\sin\left(\ldots\right)dx\right) dx\right) dx$

$-\log(c-x)=\int \exp\left(\int \exp\left(\int \exp\left(\ldots \right) dx \right) dx \right) dx$

$1/(c-x)=\int \left(\int \left(\int \left(\ldots \right)^2 dx \right)^2 dx \right)^2 dx$

And if you want a real mind-bender, use the Lambert W function:

$I(x)=\int W\left(\int W\left(\int W\left(\ldots \right) dx \right) dx \right) dx$ , then $x=\int_1^{I(x)}1/W(t) dt + c$ .

(that is, you get an implicit but well defined expression for the (x,I(x)) values. With Lambert, the x and y axes always tend to switch place).

[And yes, convergence is handwavy in this essay. I think the best way of approaching it is to view the values of these integrals as the functions invariant under the functional consisting of the integral and its repeated function: whether nearby functions are attracted to it (or not) under repeated application of the functional depends on the case. ]

“A lump of cadmium”

Cadmium crystal and metal. From Wikimedia Commons, Cc: creator Alchemist-hp 2010. — Cadmium crystal and metal. From Wikimedia Commons, creator Alchemist-hp 2010.

Stuart Armstrong sent me this email:

I have a new expression: “a lump of cadmium”.

Background: in WW2, Heisenberg was working on the German atomic reactor project (was he bad? see the fascinating play “Copenhagen” to find out!). His team almost finished a nuclear reactor. He thought that a reaction with natural uranium would be self-limiting (spoiler: it wouldn’t), so had no cadmium control rods or other means of stopping a chain reaction.

But, no worries: his team has “a lump of cadmium” that they could toss into the reactor if things got out of hand. So, now, if someone has a level of precaution woefully inadequate to the risk at hand, I will call it a lump of cadmium.

(Based on German Nuclear Program Before and During World War II by Andrew Wendorff)

It reminds me of the story that SCRAM (emergency nuclear reactor shutdowns) stands for “Safety Control Rod Axe Man“, a guy standing next to the rope suspending the control rods with an axe, ready to cut it. It has been argued it was liquid cadmium solution instead. Still, in the US project they did not assume the reaction was self stabilizing.

Going back to the primary citation, we read:

To understand it we must say something about Heisenberg’s concept of reactor design. He persuaded himself that a reactor designed with natural uranium and, say, a heavy water moderator would be self-stabilizing and could not run away. He noted that U(238) has absorption resonances in the 1-eV region, which means that a neutron with this kind of energy has a good chance of being absorbed and thus removed from the chain reaction. This is one of the challenges in reactor design—slowing the neutrons with the moderator without losing them all to absorption. Conversely, if the reactor begins to run away (become supercritical) , these resonances would broaden and neutrons would be more readily absorbed. Moreover, the expanding material would lengthen the mean free paths by decreasing the density and this expansion would also stop the chain reaction. In short, we might experience a nasty chemical explosion but not a nuclear holocaust. Whether Heisenberg realized the consequences of such a chemical explosion is not clear. In any event, no safety elements like cadmium rods were built into Heisenberg’s reactors. At best, a lump of cadmium was kepton hand in case things threatened to get out of control. He also never considered delayed neutrons, which, as we know, play an essential role in reactor safety. Because none of Heisenberg’s reactors went critical, this dubious strategy was never put to the test.

(Jeremy Bernstein, Heisenberg and the critical mass. Am. J. Phys. 70, 911 (2002); http://dx.doi.org/10.1119/1.1495409)

This reminds me a lot of the modelling errors we discuss in the “Probing the improbable” paper, especially of course the (ahem) energetic error giving Castle Bravo 15 megatons of yield instead of the predicted 4-8 megatons. Leaving out Li(7) from the calculations turned out to leave out the major contributor of energy.

Note that Heisenberg did have an argument for his safety, in fact two independent ones! The problem might have been that he was thinking in terms of mostly U(238) and then getting any kind of chain reaction going would be hard, so he was biased against the model of explosive chain reactions (but as the Bernstein paper notes, somebody in the project had correct calculations for explosive critical masses). Both arguments were flawed when dealing with reactors enriched in U(235). Coming at nuclear power from the perspective of nuclear explosions on the other hand makes it natural to consider how to keep things from blowing up.

We may hence end up with lumps of cadmium because we approach a risk from the wrong perspective. The antidote should always be to consider the risks from multiple angles, ideally a few adversarial ones. The more energy, speed or transformative power we expect something to produce, the more we should scrutinize existing safeguards for them being lumps of cadmium. If we think our project does not have that kind of power, we should both question why we are even doing it, and whether it might actually have some hidden critical mass.

The 12 threats of xrisk

The Global Challenges Foundation has (together with FHI) produced a report on the 12 risks that threaten civilization.

And, yes, the use of “infinite impact” grates on me – it must be interepreted as “so bad that it is never acceptable”, a ruin probability, or something similar, not that the disvalue diverges. But the overall report is a great start on comparing and analysing the big risks. It is worth comparing it with the WEF global risk report, which focuses on people’s perceptions of risk. This one aims at looking at what risks are most likely/impactful. Both try to give reasons and ideas for how to reduce the risks. Hopefully they will also motivate others to make even sharper analysis – this is a first sketch of the domain, rather than a perfect roadmap. Given the importance of the issues, it is a bit worrying that it has taken us this long.

Gamma function surfaces

The gamma function has a long and interesting history (check out (Davis 1963) excellent review), but one application does not seem to have shown up: minimal surfaces.

A minimal surface is one where the average curvature is always zero; it bends equally in two opposite directions. This is equivalent to having the (locally) minimal area given its boundary: such surfaces are commonly seen as soap films stretched from frames. There exists a rich theory for them, linking them to complex analysis through the Enneper-Weierstrass representation: if you have a meromorphic function g and an analytic function f such that $fg^2$ is holomorphic, then

$X(z)=\Re\left(\int_{z_0}^z f(1-g^2)/2 dz\right)$
$Y(z)=\Re\left(\int_{z_0}^z if(1+g^2)/2 dz\right)$
$Z(z)=\Re\left(\int_{z_0}^z fg dz\right)$

produces a minimal surface $(X(z),Y(z),Z(z))$ .

When plugging in the hyperbolic tangent as g and using f=1 I got a new and rather nifty surface a few years back. What about plugging in the gamma function? Let $f=1, g=\Gamma(z)$ .

We integrate from the regular point $z_0=1$ to different points $z$ in the complex plane. Let us start with the simple case of $\Re(z)>1/2$ .

Gamma function minimal surface for z in 0.5<Re(z)<3.5, -8<Im(z)<8. Color denotes Re(z). — Gamma function minimal surface for z in 0.5<Re(z)<3.5, -8<Im(z)

The surface is a billowing strip, and as we include z with larger and larger real parts the amplitude of the oscillations grow rapidly, making it self-intersect. The behaviour is somewhat similar to the Catalan minimal surface, except that we only get one period. If we go to larger imaginary parts the surface approaches a horizontal plane. OK, the surface is a plane with some wild waves, right?

Not so fast, we have not looked at the mess for Re(z)<0. First, let’s examine the area around the z=0 singularity. Since the values of the integrand blows up close to it, they produce a surface expanding towards infinity – very similar to a catenoid. Indeed, catenoid ends tend to show up where there are poles. But this one doesn’t close exactly: for re(z)<0 there is some overshoot producing a self-intersecting plane-like strip.

Gamma function minimal surface close to the z=0 singularity. Colour denotes Re(z). Integration contours from 1 to z run clockwise for Im(z)0. — Gamma function minimal surface close to the z=0 singularity. Colour denotes Re(z). Integration contours from 1 to z run clockwise for Im(z)<0 and counterclockwise for Im(z)>0.

The problem is of course the singularity: when integrating in the complex plane we need to avoid them, and depending on the direction we go around them we can get a complex phase that gives us an entirely different value of the function. In this case the branch cut corresponds to the real line: integrating clockwise or counter-clockwise around z=0 to the same z gives different values. In fact, a clockwise turn adds [3.6268i, 3.6268, 6.2832i] (which looks like $\gamma\pi$ – a rather neat residue!) to the coordinates: a translation in the positive y-direction. If we extend the surface by going an extra turn clockwise or counterclockwise a number of times, we get copies that attach seamlessly.

Gamma minimal surface extended by integration paths between the -1 and 0 singularities (blue patches).

Gamma minimal surface patch that can be repeated by translation along the y-axis. Colour denotes Re(z).

OK, we have a surface with some planar strips that turn wobbly and self-intersecting in the x-direction, with elliptic catenoid ends repeating along the y-direction due to the z=0 singularity. Going down the negative x-direction things look plane between the catenoids… except of course for the catenoids due to all the other singularities for $z=-1,-2,\ldots$ . They also introduce residues along the y-direction, but different ones from the z=0 – their extensions of the surface will be out of phase with each other, making the fully extended surface fantastically self-intersecting and confusing.

Gamma function minimal surface extended by integrating around poles.

So, I think we have a simple answer to why the gamma function minimal surface is not well known: it is simply too messy and self-intersecting.

Of course, there may be related nifty surfaces. $1/\Gamma(z)$ is nicely behaved and looks very much like the Enneper surface near zero, with “wings” that oscillate ever more wildly as we move towards the negative reals. No doubt there are other beautiful things to look for in the vicinity.

Andart II

Part of Anders' Exoself