In physics inverse square forces are among the most reliable things. You can trust that electric and gravitational fields from monopole charges decay like . Sure, dipoles and multipoles may add higher order terms, and extended conductors like wires and planes produce other behaviour. But most of us think we can trust the
behaviour for spherical objects.
I was surprised to learn that this is not at all true recently when a question at the Astronomy Stack Exchange asked about whether gravity changes near the surface of dense objects.
Electromagnetism does not quite obey the inverse square law
The cause was this paper by John Lekner, that showed that there can be attraction between conductive spheres even when they have the same charge! (Popular summary in Nature by Philip Ball) The “trick” here is that when the charged spheres approach each other the charges on the surface redistribute themselves which leads to a polarization. Near the the other sphere charges are pushed away, and if one sphere has a different radius from the other the “image charge” can be opposite, leading to a net attraction.
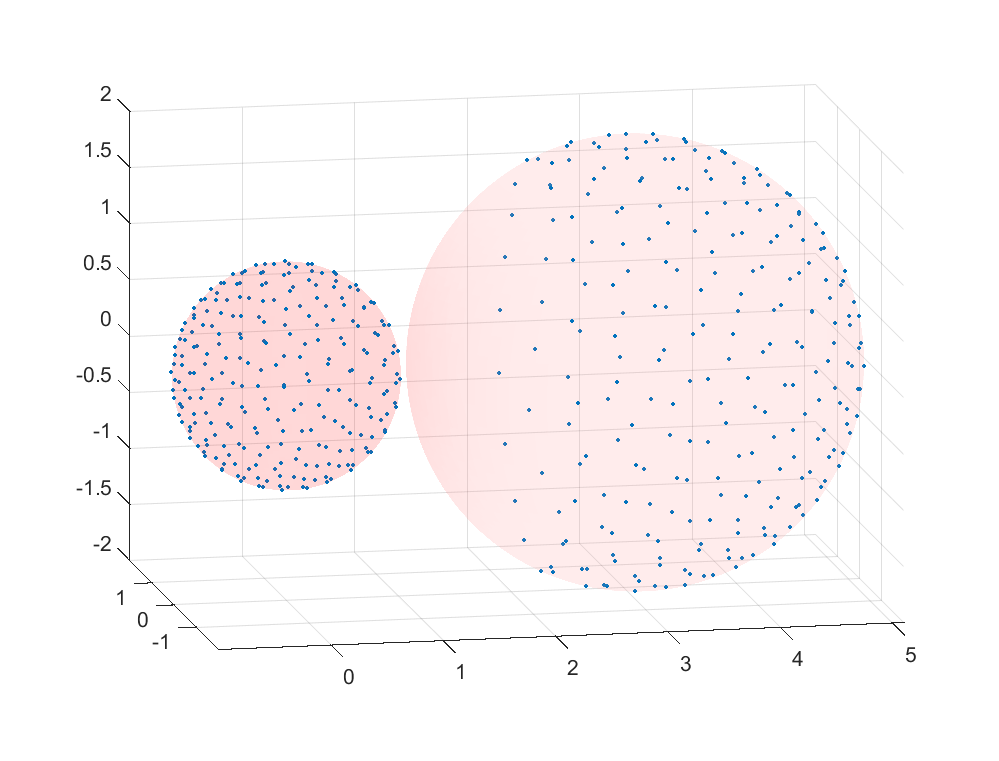
The formulas in the paper are fairly non-intuitive, so I decided to make an approximate numeric model. I put 500 charges on two spheres (radius 1.0 and 2.0) and calculated the mutual electrostatic repulsion/attraction moving them along the surface. Iterate until it stabilizes, then calculate the overall force on one of the spheres.
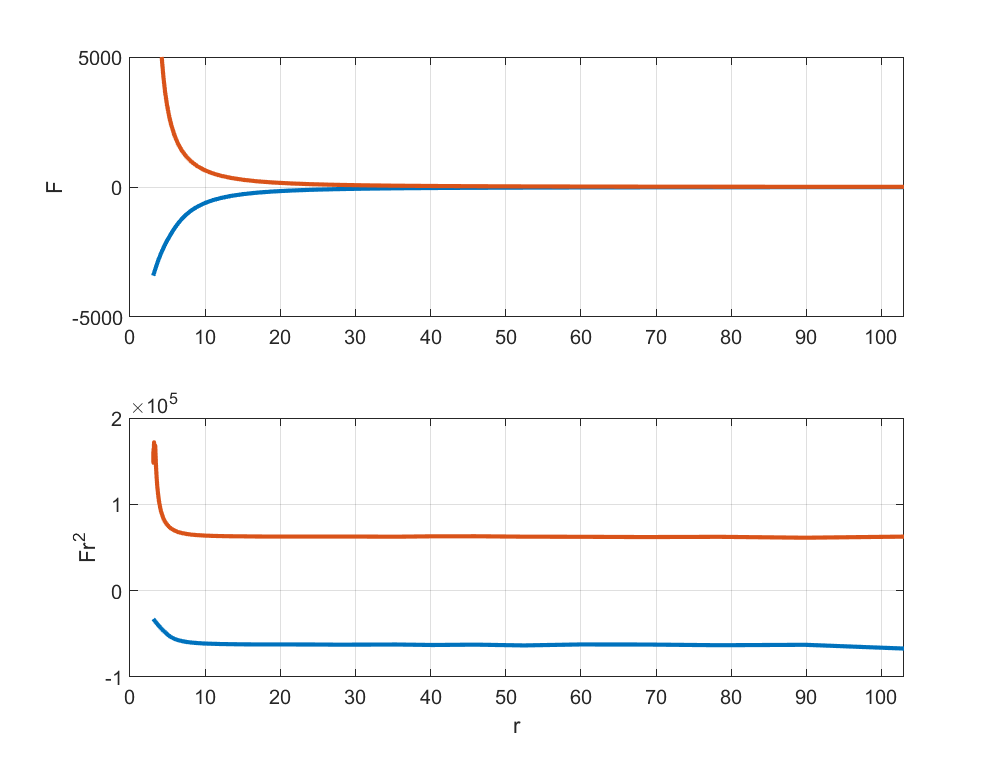
The result is indeed that the law fails as the spheres approach each other. The force times squared distance is constant until they get within a few radii, and then the equally charged sphere begins to experience less repulsion and the oppositely charged spheres more attraction than expected. My numerical method is too sloppy to do a really good job of modelling the near-touching phenomena, but it is enough to show that that the inverse square effect is not true for conductors close enough.
Gravity doesn’t obey the inverse square law either
My answer to the question was along the same lines: if two spherical bodies get close to each other they are going to deform, and this will also affect the force between them. In this case it is not charges moving on the surface, but rather gravitational and tidal distortion turning them into ellipsoids. Strictly speaking, they will turn into more general teardrop shapes, but we can use the ellipsoid as an approximation. If they have fixed centres of mass they will be prolate ellipsoids, while if they are orbiting each other they would be general three-axis ellipsoids.
Calculating the gravitational field of an ellipsoid has been done and has a somewhat elegant answer that unfortunately needs to be expressed terms of special functions. The gravitational potential in the system is just the sum of the potentials from both ellipsoids. The equilibrium shapes would correspond to ellipsoids with the same potential along their entire surface; maybe there is an explicit solution, but it does look likely to be an algebraic mess of special functions.
I did a numeric exploration instead. To find the shape I started with spheres and adjusted the semi-major axis (while preserving volume) so the potential along the surface became more equal at the poles. After a few iterations this gives a self-consistent shape. Then I calculated the force (the derivative of the potential) due to this shape on the other mass.
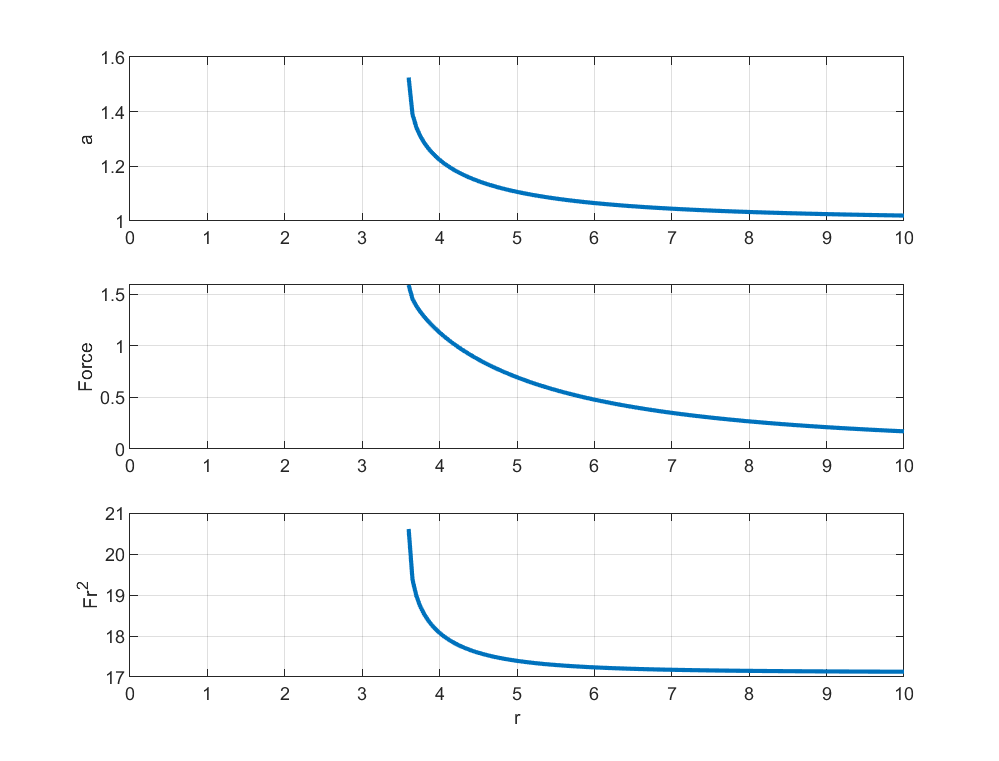
The result is indeed that the force increases faster than as the bodies approach each other, since they elongate and eventually merge (a bit before this they will deviate from my ellipsoidal assumption).
This was the Newtonian case. General relativity is even messier. In intense gravitational fields space-time is curved and expanded, making even the meaning of the distance in the inverse square law problematic. For black holes the Paczyński–Wiita potential is an approximation of the potential, and it deviates from the potential as
(where
is the Schwarzschild radius). It makes the force increase faster than the classical potential as we approach
.
Normally we assume that charges and masses stay where they are supposed to be, just as we prefer to reason as if objects are perfectly rigid or well described by point masses. In many situations this stops being true and then the effective forces can shift as the objects and their charges shift around.
Strongly disagree with your interpretation. 🙂
It’s not that the inverse square law is wrong, it’s that you cannot necessarily treat a bunch of small particles as one big particle.
Yes, that is my meaning too.