Bobby Azarian writes in The Atlantic about Apeirophobia: The Fear of Eternity. This is the existential vertigo experienced by some when considering everlasting life (typically in a religious context), or just the infinite. Pascal’s Pensées famously touches on the same feeling: “The eternal silence of these infinite spaces frightens me.” For some this is upsetting enough that it actually count as a specific phobia, although in most cases it seems to be more a general unease.

Fearing immortality

I found the concept relevant since yesterday I had a conversation with a philosopher arguing against life extension. Many of her arguments were familiar: they come up again and again if you express a positive view of longevity. It is interesting to notice that many other views do not elicit the same critical response. Suggest a future in space and some think it might be wasteful or impossible, but rarely with the same tenaciousness as life extension. As soon as one rational argument is disproven another one takes its place.

In the past I have usually attributed this to ego defence and maybe terror management. We learn about our mortality when we are young and have to come up with a way of handling it: ignoring it, denying it by assuming eternal hereafters, that we can live on through works or children, various philosophical solutions, concepts of the appropriate shape of our lives, etc. When life extension comes up, this terror management or self image is threatened and people try to defend it – their emotional equilibrium is risked by challenges to the coping strategy (and yes, this is also true for transhumanists who resolve mortality by hoping for radical life extension: there is a lot of motivated thinking going on in defending the imminent breakthroughs against death, too). While “longevity is disturbing to me” is not a good argument it is the motivator for finding arguments that can work in the social context. This is also why no amount of knocking down these arguments actually leads anywhere: the source is a coping strategy, not a rationally consistent position.

However, the apeirophobia essay suggests a different reason some people argue against life extension. They are actually unsettled by indefinite or infinite lives. I do not think everybody who argues has apeirophobia, it is probably a minority fear (and might even be a different take on the fear of death). But it is a somewhat more respectable origin than ego defence.

When I encounter arguments for the greatness of finite and perhaps short spans of life, I often rhetorically ask – especially if the interlocutor is from a religious worldview – if they think people will die in Heaven. It is basically Sappho’s argument (“to die is an evil; for the gods have thus decided. For otherwise they would be dying.”) Of course, this rarely succeeds in convincing anybody but it tends to throw a spanner in the works. However, the apeirophobia essay actually shows that some religious people may have a somewhat consistent fear that eternal life in Heaven isn’t a good thing. I respect that. Of course, I might still ask why God in their worldview insists on being eternal, but even I can see a few easy ways out of that issue (e.g. it is a non-human being not affected by eternity in the same way).

Arbitrariness

As I often have to point out, I do not believe immortality is a thing. We are finite beings in a random universe, and sooner or later our luck runs out. What to aim for is indefinitely long lives, lives that go on (with high probability) until we no longer find them meaningful. But even this tends to trigger apeirophobia. Maybe one reason is the indeterminacy: there is nothing pre-set at all.

Pascal’s worry seem to be not just the infinity of the spaces but also their arbitrariness and how insignificant we are relative to them. The full section of the Pensées:

205: When I consider the short duration of my life, swallowed up in the eternity before and after, the little space which I fill, and even can see, engulfed in the infinite immensity of spaces of which I am ignorant, and which know me not, I am frightened, and am astonished at being here rather than there; for there is no reason why here rather than there, why now rather than then. Who has put me here? By whose order and direction have this place and time been allotted to me? Memoria hospitis unius diei prætereuntis.

206: The eternal silence of these infinite spaces frightens me.

207: How many kingdoms know us not!

208: Why is my knowledge limited? Why my stature? Why my life to one hundred years rather than to a thousand? What reason has nature had for giving me such, and for choosing this number rather than another in the infinity of those from which there is no more reason to choose one than another, trying nothing else?

Pascal is clearly unsettled by infinity and eternity, but in the Pensées he tries to resolve this psychologically: since he trusts God, then eternity must be a good thing even if it is hard to bear. This is a very different position from my interlocutor yesterday, who insisted that it was the warm finitude of a human life that gave life meaning (a view somewhat echoed in Mark O’Connell’s To Be a Machine). To Pascal apeirophobia was just another challenge to become a good Christian, to the mortalist it is actually a correct, value-tracking intuition.

Apeirophobia as a moral intuition

I have always been sceptical of psychologizing why people hold views. It is sometimes useful for emphatizing with them and for recognising the futility of knocking down arguments that are actually secondary to a core worldview (which it may or may not be appropriate to challenge). But it is easy to make mistaken guesses. Plus, one often ends up in the “sociological fallacy”: thinking that since one can see non-rational reasons people hold a belief then that belief is unjustified or even untrue. As Yudkowsky pointed out, forecasting empirical facts by psychoanalyzing people never works. I also think this applies to values, insofar they are not only about internal mental states: that people with certain characteristics are more likely to think something has a certain value than people without the characteristic only gives us information about the value if that characteristic somehow correlates with being right about that kind of values.

Feeling apeirophobia does not tell us that infinity is bad, just as feeling xenophobia does not tell us that foreigners are bad. Feeling suffering on the other hand does give us direct knowledge that it is intrinsically aversive (it takes a lot of philosophical footwork to construct an argument that suffering is actually OK). Moral or emotional intuitions certainly can motivate us to investigate a topic with better intellectual tools than the vague unease, conservatism or blind hope that started the process. The validity of the results should not depend on the trigger since there is no necessary relation between the feeling and the ethical state of the thing triggering it: much of the debate about “the wisdom of repugnance” is clarifying when we should expect the intuition to overwhelm the actual thinking and when they are actually reliable. I always get very sceptical when somebody claims their intuition comes from a innate sense of what the good is – at least when it differs from mine.

Would people with apeirophobia have a better understanding of the value of infinity than somebody else? I suspect apeirophobes are on average smarter and/or have a higher need for cognition, but this does not imply that they get things right, just that they think more and more deeply about concepts many people are happy to gloss over. There are many smart nonapeirophobes too.

A strong reason to be sceptical of apeirophobic intuitions is that intuitions tend to work well when we have plenty of experience to build them from, either evolutionarily or individually. Human practical physics intuitions are great for everyday objects and speeds, and progressively worsens as we reach relativistic or quantum scales. We do not encounter eternal life at all, and hence we should be very suspicious about the validity of aperirophobia as a truth-tracking innate signal. Rather, it is triggered when we become overwhelmed by the lack of references to infinity in our lived experience or we discover the arbitrarily extreme nature of “infinite issues” (anybody who has not experienced vertigo when they understood uncountable sets?) It is a correct signal that our minds are swimming above an abyss we do not know but it does not tell us what is in this abyss. Maybe it is nice down there? Given our human tendency to look more strongly for downsides and losses than positives we will tend to respond to this uncertainty by imagining diffuse worst case scenario monsters anyway.

Bad eternities

I do not think I have apeirophobia, but I can still see how chilling belief in eternal lives can be. Unsong’s disutility-maximizing Hell is very nasty, but I do not think it exists. I am not worried about Eternal Returns: if you chronologically live forever but actually just experience a finite length loop of experiences again and again then it makes sense to say that your life just that long.

My real worry is quantum immortality: from a subjective point of view one should expect to survive whatever happen in a multiverse situation, since one cannot be aware in those branches where one died. The problem is that the set of nice states to be in is far smaller than the set of possible states, so over time we should expect to end up horribly crippled and damaged yet unable to die. But here the main problem is the suffering and reduction of circumstances, not the endlessness.

There is a problem with endlessness here though: since random events play a decisive role in our experienced life paths it seems that we have little control over where we end up and that whatever we experience in the long run is going to be wholly determined by chance (after all, beyond 10¹⁰⁰ years or more we will all have to be a succession of Boltzmann brains). But the problem seems to be more  the pointlessness that emerges from this chance than that it goes on forever: a finite randomised life seems to hold little value, and as Tolstoy put it, maybe we need infinite subjective lives where past acts matter to actually have meaning. I wonder what apeirophobes make of Tolstoy?

Embracing the abyss

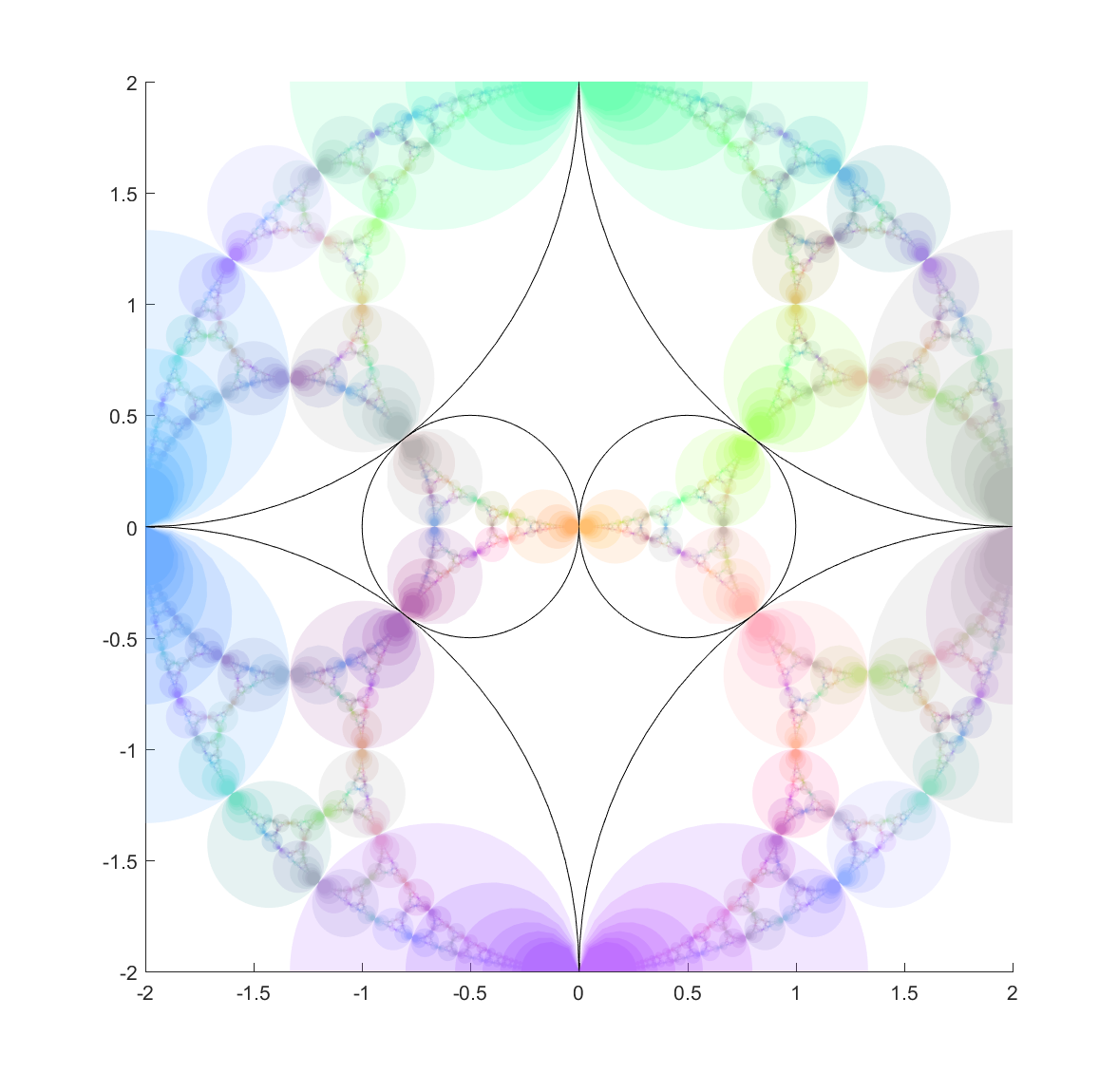
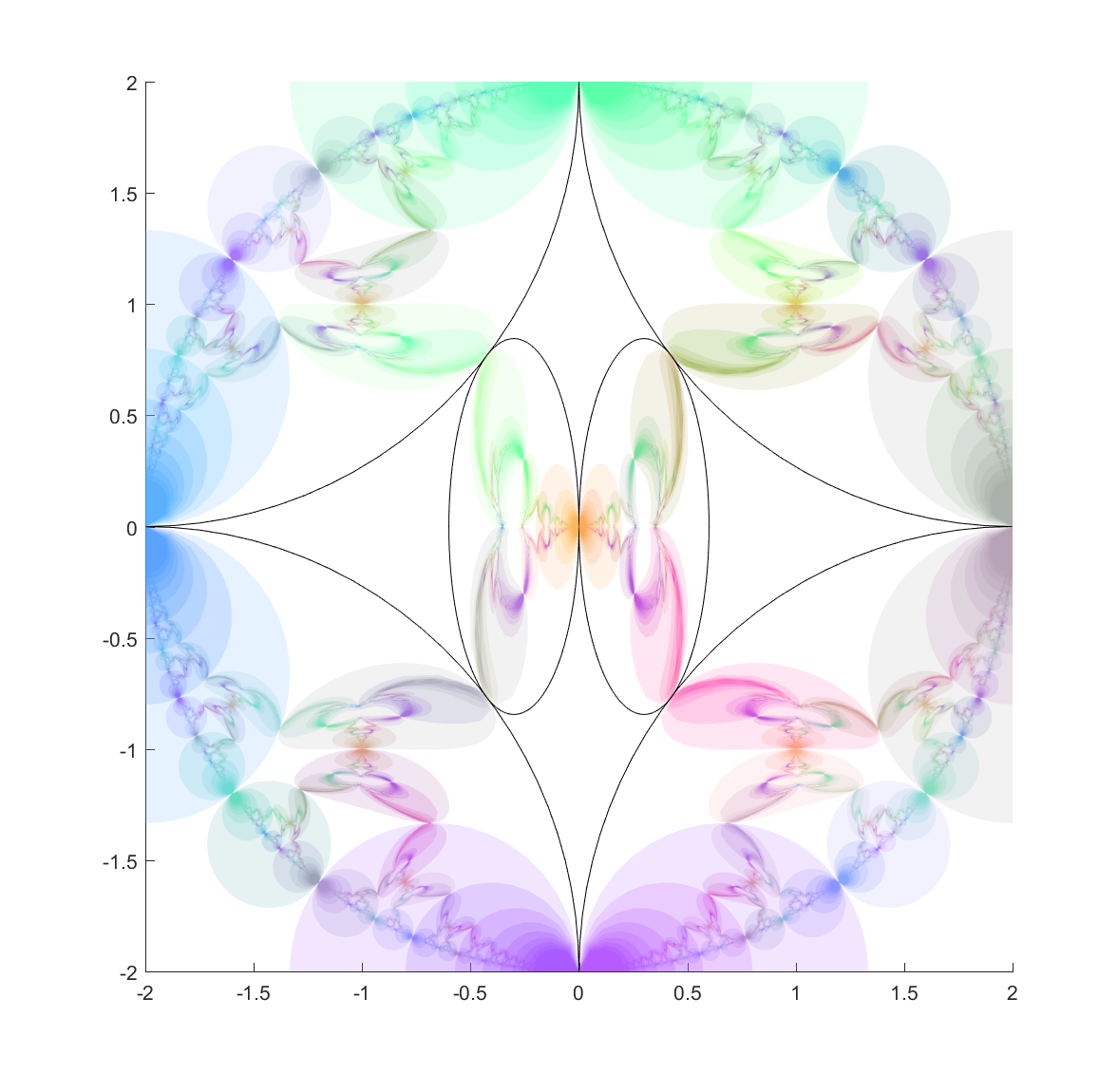
My recommendation to apeirophobes is not to take Azarian’s advice and put eternity out of mind, but instead to embrace it in a controllable way. Learn set theory and the paradoxes of infinity. And then look at the time interval 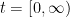and realise it can be mapped into the interval (e.g. by 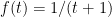). From the infinite perspective any finite length of life is equal. But infinite spans can be manipulated too: in a sense they are also all the same. The infinities hide within what we normally think of as finite.

I suspect Pascal would have been delighted if he knew this math. However, to him the essential part was how we turn intellectual meditation into emotional or existential equilibrium:

Let us therefore not look for certainty and stability. Our reason is always deceived by fickle shadows; nothing can fix the finite between the two Infinites, which both enclose and fly from it.

If this be well understood, I think that we shall remain at rest, each in the state wherein nature has placed him. As this sphere which has fallen to us as our lot is always distant from either extreme, what matters it that man should have a little more knowledge of the universe? If he has it, he but gets a little higher. Is he not always infinitely removed from the end, and is not the duration of our life equally removed from eternity, even if it lasts ten years longer?

In comparison with these Infinites all finites are equal, and I see no reason for fixing our imagination on one more than on another. The only
comparison which we make of ourselves to the finite is painful to us.

In the end it is we who make the infinite frightening or the finite painful. We can train ourselves to stop it. We may need very long lives in order to grow to do it well, though.