
XKCD joked about the problem of secure generation of random 32 bit numbers by rolling a 65536-sided die. Such a die would of course be utterly impractical, but could you actually make a polyhedron that when rolled is a fair dice with 65536 equally likely outcomes?
The curse of wrong number of faces
I immediately tweeted one approach: take a d8 (octahedron), and subdivide each triangle recursively into 4 equal ones, projecting out to a sphere seven times. Then take the dual (vertices to faces, faces to vertices). The subdivision generates triangular faces. Each face has 3 vertices, shared between 6 faces, so the total number of vertices is 65536, and they become faces of my die.
This is wrong, as Greg Egan himself pointed out. (Note to self: never do math after midnight)
Euler’s formula states that Since each face on the subdivided d8 has three edges, shared by two sides
. So
. With
I get
… two vertices too much, which means that after dualization I end up with a d65538 intead of a d65536!
This is of course hilariously cursed. It will look almost perfect, but very rarely give numbers outside the expected range.
(What went wrong? My above argument ignored that some vertices – the original polyhedron corners – are different from others.)
Tim Freeman suggested an eminently reasonable approach: start with a tetrahedron, subdivide triangles 7 times with projection outwards, and you end up with a d65536. With triangular sides rather than the mostly hexagonal ones in the cartoon.
The curse of unfairness
But it gets better: when you subdivide a triangle the new vertices are projected out to the surrounding sphere. But that doesn’t mean the four new triangles have the same area. So the areas of the faces are uneven, and we have an unfair die.
 Coloring the sides by relative area shows the fractal pattern of areas.
Coloring the sides by relative area shows the fractal pattern of areas.
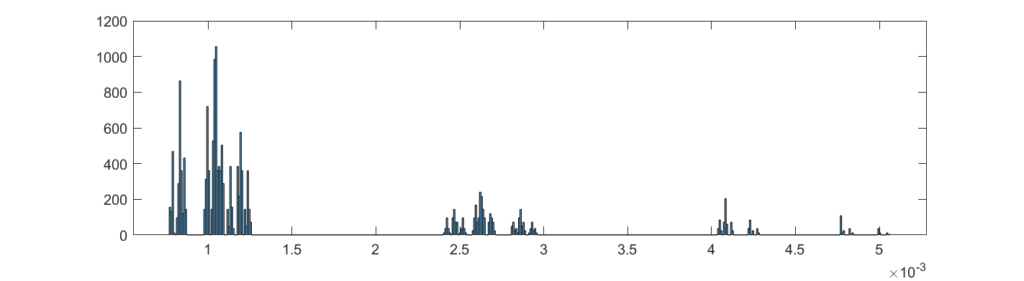 Plotting a histogram of areas show the fractal unevenness. The biggest face has 6.56 times area of the smallest face, so it is not a neglible bias.
Plotting a histogram of areas show the fractal unevenness. The biggest face has 6.56 times area of the smallest face, so it is not a neglible bias.
One way of solving this is to move the points laterally along the sphere surface to equalize the areas. One can for example use Lloyd’s algorithm. There are many other ways people distribute points evenly on spheres that might be relevant. But subtly unfair giant dice have their own charm.
Unequal dice
Note that dice with different face areas can also be fair. Imagine a n-sided prism with length . If
the probability of landing on one of the end polygons
while for each of the sides it is
(and by symmetry they are all equal). If
then the probability instead approaches 1 and the side probability approaches 0. So by continuity, in between there must be a
where the probability of landing on one of the ends equals the probability of landing on one of the sides. There is no reason for the areas to be equal.
Indeed, as discussed in this video, the value of depends on the dice throwing dynamics.
Dice that are fair by symmetry (and hence under any reasonable throwing dynamics) always have to have an even number of sides and belong to certain symmetry groups (Diaconis & Keller 1989).
The maybe-curse of the d(65536!)
A cool way to handle an unfair die is if the assignment of the numbers to the faces are completely scrambled between each roll. It does not matter how uneven the probabilities are, since after being scrambled once the probability of any number being on the most likely face will be the same.
How do you scramble fairly? The obvious approach is a gigantic d(65536!) die, marked with every possible permutation of the faces. This has sides.
But the previous problems give the nagging question: what if it is unfair?
We can of course scramble the d(65536!) with a d(65536!)! die. If that is fair, then things become fair. But what if we lack such a tremendous die, or there are no big dies that are fair?
Clearly a very unfair d(65536!) can prevent fair d65536-rolling. Imagine that the face with the unit permutation (leave all faces unchanged) has probability 1: the unfairness of the d65536 will remain. If the big die instead has probability close but not exactly 1 for the unit permutation then occasionally it will scramble faces. It could hence make the smaller die fair over long periods (but short-term it would tend to have the same bias towards some faces)… unless the other dominant faces on the d(65536!) were permutations that just moved faces with the same area to each other.
A nearly fair d(65536!) die will on the other hand scramble so that all permutation have some chance of happening, over time allowing the d65536 state to explore the full space of possibility (ergodic dynamics). This seems to be the generic case, with the unfairness-preserving dice as a peculiar special case. In general we should suspect that the typical behavior of mixing occurs: the first few permutations do not change the unfairness much, but after some (usually low) number of permutations the outcomes become very close to the uniform distribution. Hence rolling the d(65536!) die a few times between each roll of the d65536 die and permuting its face numbering accordingly will make it nearly perfectly uniform, assuming the available permutations are irreducible and aperiodic, and that we make enough extra rolls.
How many extra rolls are needed? Suppose all possible permutations are available on the d(65536!) die with nonzero probability. We want to know how many samples from it are needed to make their concatenation nearly uniformly distributed over the 65536! possible ones. If we are lucky the dynamics of the big die creates “rapid mixing dynamics” where this happens after a polynomial times a logarithm steps. Typically the time scales as where
is the second largest eigenvalue of the transition matrix. In our case of subdividing the d4, the
quite fast as we subdivide, making the effect of a big die of this type rapidly mixing. We likely only need a handful of rolls of the d(65536!) to scramble the d65536 enough to regard it as essentially fair.
But, the curse strikes again: we likely need another subdivision scheme to make the d(65536!) die than the d65536 die – this is just a plausibility result, not a proof.
Anyway, XKCD is right that it is hard to get the random bits for cryptography. I suggest flipping coins instead.
“XKCD joked about the problem of secure generation of random 32 bit numbers by rolling a 65536-sided die”
Shouldn’t that be random 16 bit numbers?