 I have for many years been a fan of the webcomic Schlock Mercenary. Hardish, humorous military sf with some nice, long-term plotting.
I have for many years been a fan of the webcomic Schlock Mercenary. Hardish, humorous military sf with some nice, long-term plotting.
In the current plotline (some spoilers ahead) there is an enormous Chekov’s gun: Earth is surrounded by an equatorial ring of microsatellites that can reflect sunlight. It was intended for climate control, but as the main character immediately points out, it also makes an awesome weapon. You can guess what happens. That leds to an interesting question: just how effective would such a weapon actually be?
From any point on Earth’s surface only part of the ring is visible above the horizon. In fact, at sufficiently high latitudes it is entirely invisible – there you would be safe no matter what. Also, Earth likely casts a shadow across the ring that lowers the efficiency on the nightside.
I guessed, based on the appearance in some strips, that the radius is about two Earth radii (12,000 km), and the thickness about 2000 km. I did a Monte Carlo integration where I generated random ring microsatellites, checking whether they were visible above the horizon for different Earth locations (by looking at the dot product of the local normal and the satellite-location vector; for anything above the horizon this product must be possible) and were in sunlight (by checking that the distance to the Earth-Sun axis was more than 6000 km). The result is the following diagram of how much of the ring can be seen from any given location:
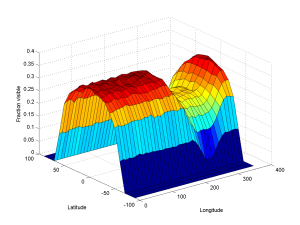
At most, 35% of the ring is visible. Even on the nightside where the shadow cuts through the ring about 25% is visible. In practice, there would be a notch cut along the equator where the ring cannot fire through itself; just how wide it would be depends on the microsatellite size and properties.
Overlaying the data on a world map gives the following footprint:
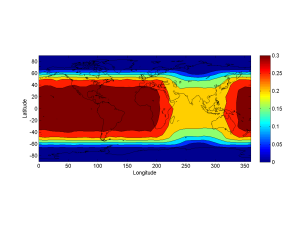
The ring is strongly visible up to 40 degrees of latitude, where it starts to disappear below the southern or northern horizon. Antarctica, northern Canada, Scandinavia and Siberia are totally safe.
This corresponds to the summer solstice, where the ring is maximally tilted relative to the Earth-Sun axis. This is when it has maximal power: at the equinoxes it is largely parallel to the sunlight and cannot reflect much at all.
The total amount of energy the ring receives is where
is the outer radius,
the inner radius, $\theta$ the tilt (between 23 degrees for the summer/winter solstice and 0 for equinoxes) and
is the solar constant, 1.361 kW/square meter. This ignores the Earth shadow. So putting in
for a New Years Eve firing, I get
Watt.
If we then multiply by 0.3 for visibility, we get 23 petawatts – is nothing to sneeze at! Of course, there will be losses, both in reflection (likely a few percent at most) and more importantly through light scattering (about 25%, assuming it behaves like normal sunlight). Now, a 17 PW beam is still pretty decent. And if you are on the nightside the shadowed ring surface can still give about 8 PW. That is about six times the energy flow in the Gulf Stream.

How destructive would such a beam be? A megaton of TNT is 4.18 PJ. So in about a second the beam could produce a comparable amount of heat. It would be far redder than a nuclear fireball (since it is essentially 6000K blackbody radiation) and the IR energy would presumably bounce around and be re-radiated, spreading far in the transparent IR bands. I suspect the fireball would quickly affect the absorption in a complicated manner and there would be defocusing effects due to thermal blooming: keeping it on target might be very hard, since energy would both scatter and reflect. Unlike a nuclear weapon there would not be much of a shockwave (I suspect there would still be one, but less of the energy would go into it).
The awesome thing about the ring is that it can just keep on firing. It is a sustainable weapon powered by renewable energy. The only drawback is that it would not have an ommminous hummmm….

Addendum 14 December: I just realized an important limitation. Sunlight comes from an extended source, so if you reflect it using plane mirrors you will get a divergent beam – which means that the spot it hits on the ground will be broad. The sun has diameter 1,391,684 km and is 149,597,871 km away, so the light spot 8000 km below the reflector will be 74 km across. This is independent of the reflector size (down to the diffraction limit and up to a mirror that is as large as the sun in the sky).

At first this sounds like it kills the ring beam. But one can achieve a better focus by clever alignment. Consider three circular footprints arranged like a standard Venn diagram. The center area gets three times the solar input as the large circles. By using more mirrors one can make a peak intensity that is much higher than the side intensity. The vicinity will still be lit up very brightly, but you can focus your devastation better than with individual mirrors – and you can afford to waste sunlight anyway. Still, it looks like this is more of a wide footprint weapon of devastation rather than a surgical knife.
You seem to have ignored the possibility of satellites bouncing light off each other. This would allow satellites without a direct line of fire to contribute to the death ray indirectly.
Yes, I did. The main reason is that the ring seems to be flat, so it is hard to bounce a beam anywhere but to your neighbour. Note that all pictures show the ring as opaque: it is dense enough to optically thick.
However, ring-bounces *can* be used to improve targeting! My Venn-diagram beam trick is still somewhat limited by the largeness of the footprints. But mirror 1 can bounce its beam to overlap with the edge of mirror 2, which sends it Earthward: this way we get a more narrow cropped beam, and summing the footprints (especially if they have the right shapes) will make the centre/periphery ratio better. The price is a lot of lost sunlight, but you will likely have enough anyway.
Where you wrote “possible” I think you meant “positive”.