During my work on the Paris talk I began to wonder whether Paul Erdős (who I used as an example of a respected academic who used cognitive enhancers) could actually have been shown to have benefited from his amphetamine use, which began in 1971 according to Hill (2004). One way of investigating is his publication record: how many papers did he produce per year before or after 1971? Here is a plot, based on Jerrold Grossman’s 2010 bibliography:
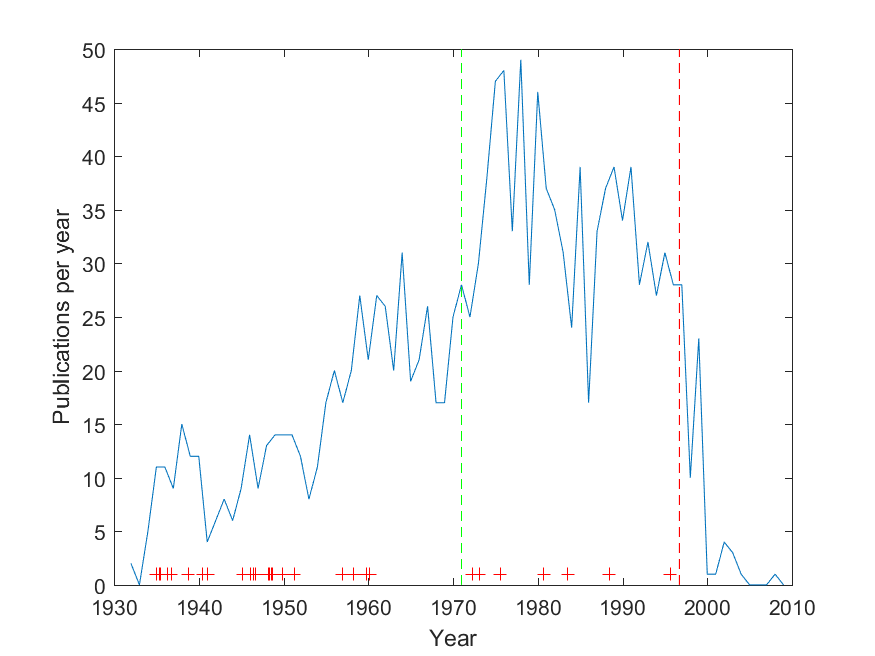
The green dashed line is the start of amphetamine use, and the red dashed life is the date of death. Yes, there is a fairly significant posthumous tail: old mathematicians never die, they just asymptote towards zero. Overall, the later part is more productive per year than the early part (before 1971 the mean and standard deviation was 14.6±7.5, after 24.4±16.1; a Kruskal-Wallis test rejects that they are the same distribution, p=2.2e-10).
This does not prove anything. After all, his academic network was growing and he moved from topic to topic, so we cannot prove any causal effect of the amphetamine: for all we know, it might have been holding him back.
One possible argument might be that he did not do his best work on amphetamine. To check this, I took the Wikipedia article that lists things named after Erdős, and tried to find years for the discovery/conjecture. These are marked with red crosses in the diagram, slightly jittered. We can see a few clusters that may correspond to creative periods: one in 35-41, one in 46-51, one in 56-60. After 1970 the distribution was more even and sparse. 76% of the most famous results were done before 1971; given that this is 60% of the entire career it does not look that unlikely to be due to chance (a binomial test gives p=0.06).
Again this does not prove anything. Maybe mathematics really is a young man’s game, and we should expect key results early. There may also have been more time to recognize and name results from the earlier career.
In the end, this is merely a statistical anecdote. It does show that one can be a productive, well-renowned (if eccentric) academic while on enhancers for a long time. But given the N=1, firm conclusions or advice are hard to draw.
Erdős’s friends worried about his drug use, and in 1979 Graham bet Erdős $500 that he couldn’t stop taking amphetamines for a month. Erdős accepted, and went cold turkey for a complete month. Erdős’s comment at the end of the month was “You’ve showed me I’m not an addict. But I didn’t get any work done. I’d get up in the morning and stare at a blank piece of paper. I’d have no ideas, just like an ordinary person. You’ve set mathematics back a month.” He then immediately started taking amphetamines again. (Hill 2004)
It certainly looks suggestive that the second largest drop occurred in 1979, the year he spent ~8% of his time off the drug.
It does, doesn’t it? But it is hard to prove anything, which is why I refrained from pointing it out.