George Dvorsky has a post on io9: 10 Horrifying Technologies That Should Never Be Allowed To Exist. It is a nice clickbaity overview of some very bad technologies:
George Dvorsky has a post on io9: 10 Horrifying Technologies That Should Never Be Allowed To Exist. It is a nice clickbaity overview of some very bad technologies:
- Weaponized nanotechnology (he mainly mentions ecophagy, but one can easily come up with other nasties like ‘smart poisons’ that creep up on you or gremlin devices that prevent technology – or organisms – from functioning)
- Conscious machines (making devices that can suffer is not a good idea)
- Artificial superintelligence (modulo friendliness)
- Time travel
- Mind reading devices (because of totalitarian uses)
- Brain hacking devices
- Autonomous robots programmed to kill humans
- Weaponized pathogens
- Virtual prisons and punishment
- Hell engineering (that is, effective production of super-adverse experiences; consider Iain M. Banks’ Surface Detail, or the various strange/silly/terrifying issues linked to Roko’s basilisk)
Some of the these technologies exist, like weaponized pathogens. Others might be impossible, like time travel. Some are embryonic like mind reading (we can decode some brainstates, but it requires spending a while in a big scanner as the input-output mapping is learned).
A commenter on the post asked “Who will have the responsibility of classifying and preventing “objectively evil” technology?” The answer is of course People Who Have Ph.D.s in Philosophy.
Unfortunately I haven’t got one, but that will not stop me.
Existential risk as evil?
I wonder what unifies this list. Let’s see: 1, 3, 7, and 8 are all about danger: either the risk of a lot of death, or the risk of extinction. 2, 9 and 10 are all about disvalue: the creation of very negative states of experience. 5 and 6 are threats to autonomy.
4, time travel, is the odd one out: George suggests that it is dangerous, but this is based on fictional examples, and that contact between different civilizations has never ended well (which is arguable: Japan). I can imagine a consistent universe with time travel might be bad for people’s sense of free will, and if you have time loops you can do super-powerful computation (getting superintelligence risk), but I do not think of any kind of plausible physics where time travel itself is dangerous. Fiction just makes up dangers to make the plot move on.
In the existential risk framework, it is worth noting that extinction is not the only kind of existential risk. We could mess things up so that humanity’s full potential never gets realized (for example by being locked into a perennial totalitarian system that is actually resistant to any change), or that we make the world hellish. These are axiological existential risks. So the unifying aspect of these technologies is that they could cause existential risk, or at least bad enough approximations.
Ethically, existential threats count a lot. They seem to have priority over mere disasters and other moral problems in a wide range of moral systems (not just consequentialism). So technologies that strongly increase existential risk without giving a commensurate benefit (for example by reducing other existential risks more – consider a global surveillance state, which might be a decent defence against people developing bio-, nano- and info-risks at the price of totalitarian risk) are indeed impermissible. In reality technologies have dual uses and the eventual risk impact can be hard to estimate, but the principle is reasonable even if implementation will be a nightmare.
Messy values
However, extinction risk is an easy category – even if some of the possible causes like superintelligence are weird and controversial, at least extinct means extinct. The value and autonomy risks are far trickier. First, we might be wrong about value: maybe suffering doesn’t actually count morally, we just think it does. So a technology that looks like it harms value badly like hell engineering actually doesn’t. This might seem crazy, but we should recognize that some things might be important but we do not recognize them. Francis Fukuyama thought transhumanist enhancement might harm some mysterious ‘Factor X’ (i.e. a “soul) giving us dignity that is not widely recognized. Nick Bostrom (while rejecting the Factor X argument) has suggested that there might be many “quiet values” important for diginity, taking second seat to the “loud” values like alleviation of suffering but still being important – a world where all quiet values disappear could be a very bad world even if there was no suffering (think Aldous Huxley’s Brave New World, for example). This is one reason why many superintelligence scenarios end badly: transmitting the full nuanced world of human values – many so quiet that we do not even recognize them ourselves before we lose them – is very hard. I suspect that most people find it unlikely that loud values like happiness or autonomy actually are parochial and worthless, but we could be wrong. This means that there will always be a fair bit of moral uncertainty about axiological existential risks, and hence about technologies that may threaten value. Just consider the argument between Fukuyama and us transhumanists.
Second, autonomy threats are also tricky because autonomy might not be all that it is cracked up to be in western philosophy. The atomic free-willed individual is rather divorced from the actual neural and social matrix creature. But even if one doesn’t buy autonomy as having intrinsic value, there are likely good cybernetic arguments for why maintaining individuals as individuals with their own minds is a good thing. I often point to David Brin’s excellent defence of the open society where he points out that societies where criticism and error correction are not possible will tend to become corrupt, inefficient and increasingly run by the preferences of the dominant cadre. In the end they will work badly for nearly everybody and have a fair risk of crashing. Tools like surveillance, thought reading or mind control would potentially break this beneficial feedback by silencing criticism. They might also instil identical preferences, which seems to be a recipe for common mode errors causing big breakdowns: monocultures are more vulnerable than richer ecosystems. Still, it is not obvious that these benefits could not exist in (say) a group-mind where individuality is also part of a bigger collective mind.
Criteria and weasel-words
These caveats aside, I think the criteria for “objectively evil technology” could be
(1) It predictably increases existential risk substantially without commensurate benefits,
or,
(2) it predictably increases the amount of death, suffering or other forms of disvalue significantly without commensurate benefits.
There are unpredictable bad technologies, but they are not immoral to develop. However, developers do have a responsibility to think carefully about the possible implications or uses of their technology. And if your baby-tickling machine involves black holes you have a good reason to be cautious.
Of course, “commensurate” is going to be the tricky word here. Is a halving of nuclear weapons and biowarfare risk good enough to accept a doubling of superintelligence risk? Is a tiny probability existential risk (say from a physics experiment) worth interesting scientific findings that will be known by humanity through the entire future? The MaxiPOK principle would argue that the benefits do not matter or weigh rather lightly. The current gain-of-function debate show that we can have profound disagreements – but also that we can try to construct institutions and methods that regulate the balance, or inventions that reduce the risk. This also shows the benefit of looking at larger systems than the technology itself: a potentially dangerous technology wielded responsibly can be OK if the responsibility is reliable enough, and if we can bring a safeguard technology into place before the risky technology it might no longer be unacceptable.
The second weasel word is “significantly”. Do landmines count? I think one can make the case. According to the UN they kill 15,000 to 20,000 people per year. The number of traffic fatalities per year worldwide is about 1.2 million deaths – but we might think cars are actually so beneficial that it outweighs the many deaths.
Intention?
The landmines are intended to harm (yes, the ideal use is to make people rationally stay the heck away from mined areas, but the harming is inherent in the purpose) while cars are not. This might lead to an amendment of the second criterion:
(2′) The technology intentionally increases the amount of death, suffering or other forms of disvalue significantly without commensurate benefits.
This gets closer to how many would view things: technologies intended to cause harm are inherently evil. But being a consequentialist I think it let’s designers off the hook. Dr Guillotine believed his invention would reduce suffering (and it might have) but it also led to a lot more death. Dr Gatling invented his gun to “reduce the size of armies and so reduce the number of deaths by combat and disease, and to show how futile war is.” So the intention part is problematic.
Some people are concerned with autonomous weapons because they are non-moral agents making life-and-death decisions over people; they would use deontological principles to argue that making such amoral devices are wrong. But a landmine that has been designed to try to identify civilians and not blow up around them seems to be a better device than an indiscriminate device: the amorality of the decisionmaking is less of problematic than the general harmfulness of the device.
I suspect trying to bake in intentionality or other deontological concepts will be problematic. Just as human dignity (another obvious concept – “Devices intended to degrade human dignity are impermissible”) is likely a non-starter. They are still useful heuristics, though. We do not want too much brainpower spent on inventing better ways of harming or degrading people.
Policy and governance: the final frontier
In the end, this exercise can be continued indefinitely. And no doubt it will.
Given the general impotence of ethical arguments to change policy (it usually picks up the pieces and explains what went wrong once it does go wrong) a more relevant question might be how a civilization can avoid developing things it has a good reason to suspect are a bad idea. I suspect the answer to that is going to be not just improvements in coordination and the ability to predict consequences, but some real innovations in governance under empirical and normative uncertainty.
But that is for another day.
 Since I am getting married tomorrow, it is fitting that the Institute of Art and Ideas TV has just put my lecture from Hay-on-Wye this year online: Manufacturing love.
Since I am getting married tomorrow, it is fitting that the Institute of Art and Ideas TV has just put my lecture from Hay-on-Wye this year online: Manufacturing love.





 I have not been able to dig up the project documentation, but I would be astonished if there was any discussion of risk due to the experiment. After all, cooling things is rarely dangerous. We do not have any physical theories saying there could be anything risky here. No doubt there are risk assessment of liquid nitrogen or helium practical risks somewhere, but no analysis of any basic physics risks.
I have not been able to dig up the project documentation, but I would be astonished if there was any discussion of risk due to the experiment. After all, cooling things is rarely dangerous. We do not have any physical theories saying there could be anything risky here. No doubt there are risk assessment of liquid nitrogen or helium practical risks somewhere, but no analysis of any basic physics risks.



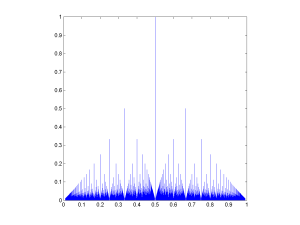
![The rational distribution of two convolved Exp[0.1] distributions.](http://aleph.se/andart2/wp-content/uploads/2014/09/trifonovexp01-300x225.png)
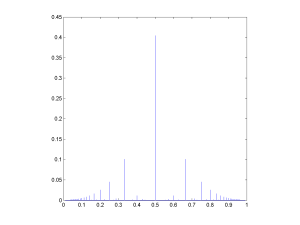
![Rational distribution of ratio between a Poisson[10] and a Poisson[5] variable.](http://aleph.se/andart2/wp-content/uploads/2014/09/trifonovpoiss105-300x225.png)