Newtonmas fractals: rose of gravity

Continuing my intermittent Newtonmas fractal tradition (2014, 2016, 2018), today I play around with a very suitable fractal based on gravity.

The problem

On Physics StackExchange NiveaNutella asked a simple yet tricky to answer question:

If we have two unmoving equal point masses in the plane (let’s say at $(\pm 1,0)$ ) and release particles from different locations they will swing around the masses in some trajectory. If we colour each point by the mass it approaches closest (or even collides with) we get a basin of attraction for each mass. Can one prove the boundary is a straight line?

User Kasper showed that one can reframe the problem in terms of elliptic coordinates and show that this implies a straight boundary, while User Lineage showed it more simply using the second constant of motion. I have the feeling that there ought to be an even simpler argument. Still, Kasper’s solution show that the generic trajectory will quasiperiodically fill a region and tend to come arbitrarily close to one of the masses.

The fractal

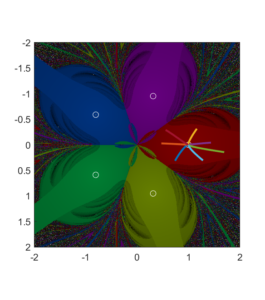
In any case, here is a plot of the basins of attraction shaded by the time until getting within a small radius $r_{trap}$ around the masses. Dark regions take long to approach any of the masses, white regions don’t converge within a given cut-off time.

The boundary is a straight line, and surrounding the simple regions where orbits fall nearly straight into the nearest mass are the wilder regions where orbits first rock back and forth across the x-axis before settling into ellipses around the masses.

The case for 5 evenly spaced masses for $r_{trap}=0.1$ and 0.01 (assuming unit masses at unit distance from origin and $G=1$ ) is somewhat prettier.

Gravity fractal for N=5, trap radius = 0.1.

Gravity fractal for N=5, trap radius = 0.01.

As $r_{trap}\rightarrow 0$ the basins approach ellipses around their central mass, corresponding to orbits that loop around them in elliptic orbits that eventually get close enough to count as a hit. The onion-like shading is due to different number of orbits before this happens. Each basin also has a tail or stem, corresponding to plunging orbits coming in from afar and hitting the mass straight. As the trap condition is made stricter they become thinner and thinner, yet form an ever more intricate chaotic web oughtside the central region. Due to computational limitations (read: only a laptop available) these pictures are of relatively modest integration times.

I cannot claim credit for this fractal, as NiveaNutella already plotted it. But it still fascinates me.

Wada basins and mille-feuille collision manifolds

These patterns are somewhat reminiscent of the classic Newton’s root-finding iterative formula fractals: several basins of attraction with a fractal border where pairs of basins encounter interleaved tiny parts of basins not member of the pair.

However, this dynamics is continuous rather than discrete. The plane is a 2D section through a 4D phase space, where starting points at zero velocity accelerate so that they bob up and down/ana and kata along the velocity axes. This also leads to a neat property of the basins of attraction: they are each arc-connected sets, since for any two member points that are the start of trajectories they end up in a small ball around the attractor mass. One can hence construct a map from $[0,1]$ to $(x,y,\dot{x},\dot{x})$ that is a homeomorphism. There are hence just N basins of attraction, plus a set of unstable separatrix points that never approach the masses. Some of these border points are just invariant (like the origin in the case of the evenly distributed masses), others correspond to unstable orbits.

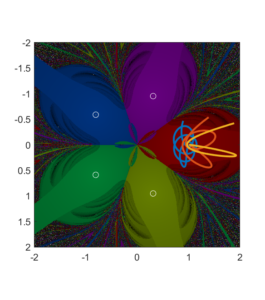
Each mass is surrounded by a set of trajectories hitting it exactly, which we can parametrize by the angle they make and the speed they have inwards when they pass some circle around the mass point. They hence form a 3D manifold $\theta \times v \times t$ where $t\in (0,\infty)$ counts the time until collision (i.e. backwards). These collision manifolds must extend through the basin of attraction, approaching the border in ever more convoluted ways as $t$ approaches $\infty$ . Each border point has a neighbourhood where there are infinitely many trajectories directly hitting one of the masses. They form 3D sheets get stacked like an infinitely dense mille-feuille cake in the 4D phase space. And typically these sheets are interleaved with the sheets of the other attractors. The end result is very much like the Lakes of Wada. Proving the boundary actually has the Wada property is tricky, although new methods look promising.

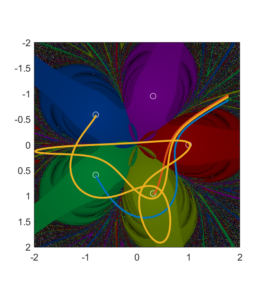
The magnetic pendulum

This fractal is similar to one I made back in 1990 inspired by the dynamics of the magnetic decision-making desk toy, a pendulum oscillating above a number of magnets. Eventually it settles over one. The basic dynamics is fairly similar (see Zhampres’ beautiful images or this great treatment). The difference is that the gravity fractal has no dissipation: in principle orbits can continue forever (but I end when they get close to the masses or after a timeout) and in the magnetic fractal the force dependency was bounded, a $K/(r^2 + c)$ force rather than the $G/r^2$ .

That simulation was part of my epic third year project in the gymnasium. The topic was “Chaos and self-organisation”, and I spent a lot of time reading the dynamical systems literature, running computer simulations, struggling with WordPerfect’s equation editor and producing a manuscript of about 150 pages that required careful photocopying by hand to get the pasted diagrams on separate pieces of paper to show up right. My teacher eventually sat down with me and went through my introduction and had me explain Poincaré sections. Then he promptly passed me. That was likely for the best for both of us.

Appendix: Matlab code

showPlot=0; % plot individual trajectories
randMass = 0; % place masses randomly rather than in circle

RTRAP=0.0001; % size of trap region
tmax=60; % max timesteps to run
S=1000; % resolution

x=linspace(-2,2,S);
y=linspace(-2,2,S);
[X,Y]=meshgrid(x,y);

N=5;
theta=(0:(N-1))*pi*2/N;
PX=cos(theta); PY=sin(theta);
if (randMass==1)
s = rng(3);
PX=randn(N,1); PY=randn(N,1);
end

clf

hit=X*0; 
hitN = X*0; % attractor basin
hitT = X*0; % time until hit
closest = X*0+100; 
closestN=closest; % closest mass to trajectory

tic; % measure time
for a=1:size(X,1)
disp(a)
for b=1:size(X,2)
[t,u,te,ye,ie]=ode45(@(t,y) forceLaw(t,y,N,PX,PY), [0 tmax], [X(a,b) 0 Y(a,b) 0],odeset('Events',@(t,y) finishFun(t,y,N,PX,PY,RTRAP^2)));

if (showPlot==1)
plot(u(:,1),u(:,3),'-b')
hold on
end

if (~isempty(te))
hit(a,b)=1;
hitT(a,b)=te;

mind2=100^2;
for k=1:N
dx=ye(1)-PX(k);
dy=ye(3)-PY(k);
d2=(dx.^2+dy.^2);
if (d2<mind2) mind2=d2; hitN(a,b)=k; end
end

end
for k=1:N
dx=u(:,1)-PX(k);
dy=u(:,3)-PY(k);
d2=min(dx.^2+dy.^2);
closest(a,b)=min(closest(a,b),sqrt(d2));

if (closest(a,b)==sqrt(d2)) closestN(a,b)=k; end
end
end

if (showPlot==1)
drawnow
pause
end
end
elapsedTime = toc

if (showPlot==0)
% Make colorful plot
co=hsv(N);
mag=sqrt(hitT);
mag=1-(mag-min(mag(:)))/(max(mag(:))-min(mag(:)));
im=zeros(S,S,3);
im(:,:,1)=interp1(1:N,co(:,1),closestN).*mag;
im(:,:,2)=interp1(1:N,co(:,2),closestN).*mag;
im(:,:,3)=interp1(1:N,co(:,3),closestN).*mag;
image(im)
end

% Gravity 
function dudt = forceLaw(t,u,N,PX,PY)
%dudt = zeros(4,1);
dudt=u;
dudt(1) = u(2);
dudt(2) = 0;
dudt(3) = u(4);
dudt(4) = 0;

dx=u(1)-PX;
dy=u(3)-PY;
d=(dx.^2+dy.^2).^-1.5;
dudt(2)=dudt(2)-sum(dx.*d);
dudt(4)=dudt(4)-sum(dy.*d);

% for k=1:N
% dx=u(1)-PX(k);
% dy=u(3)-PY(k);
% d=(dx.^2+dy.^2).^-1.5;
% dudt(2)=dudt(2)-dx.*d;
% dudt(4)=dudt(4)-dy.*d;
% end
end

% Are we close enough to one of the masses?
function [value,isterminal,direction] =finishFun(t,u,N,PX,PY,r2)
value=1000;
for k=1:N
dx=u(1)-PX(k);
dy=u(3)-PY(k);
d2=(dx.^2+dy.^2);
value=min(value, d2-r2);
end
isterminal=1;
direction=0;
end

Newtonmass fractals 2018

It is Newtonmass, and that means doing some fun math. I try to invent a new fractal or something similar every year: this is the result for 2018.

The Newton fractal is an old classic. Newton’s method for root finding iterates an initial guess $z_0$ to find a better approximation $z_{n+1}=z_{n}-f(z_{n})/f'(z_{n})$ . This will work as long as $f'(z)\neq 0$ , but which root one converges to can be sensitively dependent on initial conditions. Plotting which root a given initial value ends up with gives the Newton fractal.

The Newton-Gauss method is a method for minimizing the total squared residuals $S(\beta)=\sum_{i=1}^m r_i^2(\beta)$ when some function dependent on n-dimensional parameters $\beta$ is fitted to $m$ data points $r_i(\beta)=f(x_i;\beta)-y_i$ . Just like the root finding method it iterates towards a minimum of $S(\beta)$ : $\beta_{n+1} = \beta_n - (J^t J)^{-1}J^t r(\beta)$ where $J$ is the Jacobian $J_{ij}=\frac{\partial r_i}{\partial \beta_j}$ . This is essentially Newton’s method but in a multi-dimensional form.

So we can make fractals by trying to fit (say) a function consisting of the sum of two Gaussians with different means (but fixed variances) to a random set of points. So we can set $f(x;\beta_1,\beta_2)=(1/\sqrt{2\pi})[e^{-(x-\beta_1)^2/2}+(1/4)e^{-(x-\beta_1)^2/8}]$ (one Gaussian with variance 1 and one with 1/4 – the reason for this is not to make the diagram boringly symmetric as for the same variance case). Plotting the location of the final $\beta(50)$ (by stereographically mapping it onto a unit sphere in (r,g,b) space) gives a nice fractal:

Basins of attraction of different attractor states of Gauss-Newton's method. — Basins of attraction of different attractor states of Gauss-Newton’s method. Two Gaussian functions fitted to five random points.

Basins of attraction of different attractor states of Gauss-Newton's method. Two Gaussian functions fitted to 10 random points. — Basins of attraction of different attractor states of Gauss-Newton’s method. Two Gaussian functions fitted to 10 random points.

Basins of attraction of different attractor states of Gauss-Newton’s method. Two Gaussian functions fitted to 50 random points.

It is a bit modernistic-looking. As I argued in 2016, this is because the generic local Jacobian of the dynamics doesn’t have much rotation.

As more and more points are added the attractor landscape becomes simpler, since it is hard for the Gaussians to “stick” to some particular clump of points and the gradients become steeper.

This fractal can obviously be generalized to more dimensions by using more parameters for the Gaussians, or more Gaussians etc.

The fractality is guaranteed by the generic property of systems with several attractors that points at the border of two basins of attraction will tend to find their ways to other attractors than the two equally balanced neighbors. Hence a cut transversally across the border will find a Cantor-set of true basin boundary points (corresponding to points that eventually get mapped to a singular Jacobian in the iteration formula, like the boundary of the Newton fractal is marked by points mapped to $f'(z_n)=0$ for some n) with different basins alternating.

Merry Newtonmass!

Newtonmas fractals: conquering the second dimension!

Perturbed Newton "classic", epsilon=-3.75. — Perturbed Newton “classic”, epsilon=-3.75.

It is Newtonmas, so time to invent some new fractals.

Complex iteration of Newton’s method for finding zeros of a function is a well-known way of getting lovely filigree Julia sets: the basins of attraction of the different zeros have fractal borders.

But what if we looked at real functions? If we use a single function $f(x,y)$ the zeros will typically form a curve in the plane. In order to get discrete zeros we typically need to have two functions to produce a zero set. We can think of it as a map from R2 to R2 $F(x)=[f_1(x_1,x_2), f_2(x_1,x_2)]$ where the x’es are 2D vectors. In this case Newton’s method turns into solving the linear equation system $J(x_n)(x_{n+1}-x_n)=-F(x_n)$ where $J(x_n)$ is the Jacobian matrix ( $J_{ij}=dF_i/dx_j$ ) and $x_n$ now denotes the n’th iterate.

The simplest case of nontrivial dynamics of the method is for third degree polynomials, and we want the x- and y-directions to interact a bit, so a first try is $F=[x^3-x-y, y^3-x-y]$ . Below is a plot of the first and second components (red and green), as well as a blue plane for zero values. The zeros of the function are the three points where red, green and blue meet.

We have three zeros, one at $x=y=-\sqrt{2}$ , one at $x=y=0$ , and one at $x=y=\sqrt{2}.$ The middle one has a region of troublesomely similar function values – the red and green surfaces are tangent there.

Plot of x^3-x-y (red), y^3-x-y (green) and z=0 (blue). The zeros found using Newton's method are the points where red, green and blue meet. — Plot of x^3-x-y (red), y^3-x-y (green) and z=0 (blue). The zeros found using Newton’s method are the points where red, green and blue meet.

The resulting fractal has a decided modernist bent to it, all hyperbolae and swooshes:

Behavior of Newton's method in 2D for F=[x^3-x-y, y^3-x-y]. Color denotes value of x+y, with darkening for slow convergence. — Behavior of Newton’s method in 2D for F=[x^3-x-y, y^3-x-y]. Color denotes value of x+y, with darkening for slow convergence.

The troublesome region shows up, as well as the red and blue regions where iterates run off to large or small values: the three roots are green shades.

Why is the style modernist?

In complex iterations you typically multiply with complex numbers, and if they have an imaginary component (they better have, to be complex!) that introduces a rotation or twist. Hence baroque filaments are ubiquitous, and you get the typical complex “style”.

But here we are essentially multiplying with a real matrix. For a real 2×2 matrix to be a rotation matrix it has to have a pair of imaginary eigenvalues, and for it to at least twist things around the trace needs to be small enough compared to the determinant so that there are complex eigenvalues: $T^2/4<D$ (where $T=a+d$ and $D=ad-bc$ if the matrix has the usual $[a b; c d]$ form). So if the trace and determinant are randomly chosen, we should expect a majority of cases to be non-rotational.

Moreover, in this particular case, the Jacobian tends to be diagonally dominant (quadratic terms on the diagonal) and that makes the inverse diagonally dominant too: the trace will be big, and hence the chance of seeing rotation goes down even more. The two “knots” where a lot of basins of attraction come together are the points where the trace does vanish, but since the Jacobian is also symmetric there will not be any rotation anyway. Double guarantee.

Can we make a twisty real Newton fractal? If we start with a vanilla rotation matrix and try to find a function that produces it the simplest case is $F=[x \cos(\theta) + y \sin(\theta), x\sin(\theta)+y\cos(\theta)]$ . This is of course just a rotation by the angle theta, and it does not have very interesting zeros.

To get something fractal we need more zeros, and a few zeros in the derivatives too (why? because they cause iterates to be thrown away far from where they were, ensuring a complicated structure of the basin boundaries). One attempt is $F=[ (x^3-x-y) \cos(\theta)$ $-(y^3-x-y) \sin(\theta),$ $(x^3-x-y) \sin(\theta)+(y^3-y-x) \cos(\theta) ]$ . The result is fun, but still far from baroque:

Basins of attraction for Netwon's method of twisted cubic. theta=1. — Basins of attraction for Netwon’s method of twisted cubic. theta=1.

Basins of attraction for Netwon's method of twisted cubic. theta=0.1. — Basins of attraction for Netwon’s method of twisted cubic. theta=0.1.

The problem might be that the twistiness is not changing. So we can make $\theta=x$ to make the dynamics even more complex:

Basins of attraction with rotation proportional to x.

Quite lovely, although still not exactly what I wanted (sounds like a Christmas present).

Back to the classics?

It might be easier just to hide the complex dynamics in an apparently real function like $F=[x^3-3xy^2-1, 3x^2y-y^3]$ (which produces the archetypal $f(z)=z^3-1$ Newton fractal).

Newton fractal for F=[x^3-3xy^2-1, 3x^2y-y^3]. Red and blue circles mark regions where iterates venture far from the origin.

It is interesting to see how much perturbing it causes a modernist shift. If we use $F=[x^3-3xy^2-1 + \epsilon x, 3x^2y-y^3]$ , then for $\epsilon=1$ we get:

Perturbed z^3-1 Newton iteration, epsilon=1.

As we make the function more perturbed, it turns more modernist, undergoing a topological crisis for epsilon between 3.5 and 4:

Perturbed z^3-1 Newton iteration, epsilon=2.

Perturbed z^3-1 Newton iteration, epsilon=3.

Perturbed z^3-1 Newton iteration, epsilon=3.5.

Perturbed z^3-1 Newton iteration, epsilon=4.

In the end, we can see that the border between classic baroque complex fractals and the modernist swooshy real fractals is fuzzy. Or, indeed, fractal.

Andart II

Part of Anders' Exoself

newton

Newtonmas fractals: rose of gravity

Newtonmass fractals 2018

Newtonmas fractals: conquering the second dimension!

Why is the style modernist?

Back to the classics?