
It is Newtonmas, so time to invent some new fractals.
Complex iteration of Newton’s method for finding zeros of a function is a well-known way of getting lovely filigree Julia sets: the basins of attraction of the different zeros have fractal borders.
But what if we looked at real functions? If we use a single function the zeros will typically form a curve in the plane. In order to get discrete zeros we typically need to have two functions to produce a zero set. We can think of it as a map from R2 to R2
where the x’es are 2D vectors. In this case Newton’s method turns into solving the linear equation system
where
is the Jacobian matrix (
) and
now denotes the n’th iterate.
The simplest case of nontrivial dynamics of the method is for third degree polynomials, and we want the x- and y-directions to interact a bit, so a first try is . Below is a plot of the first and second components (red and green), as well as a blue plane for zero values. The zeros of the function are the three points where red, green and blue meet.
We have three zeros, one at , one at
, and one at
The middle one has a region of troublesomely similar function values – the red and green surfaces are tangent there.
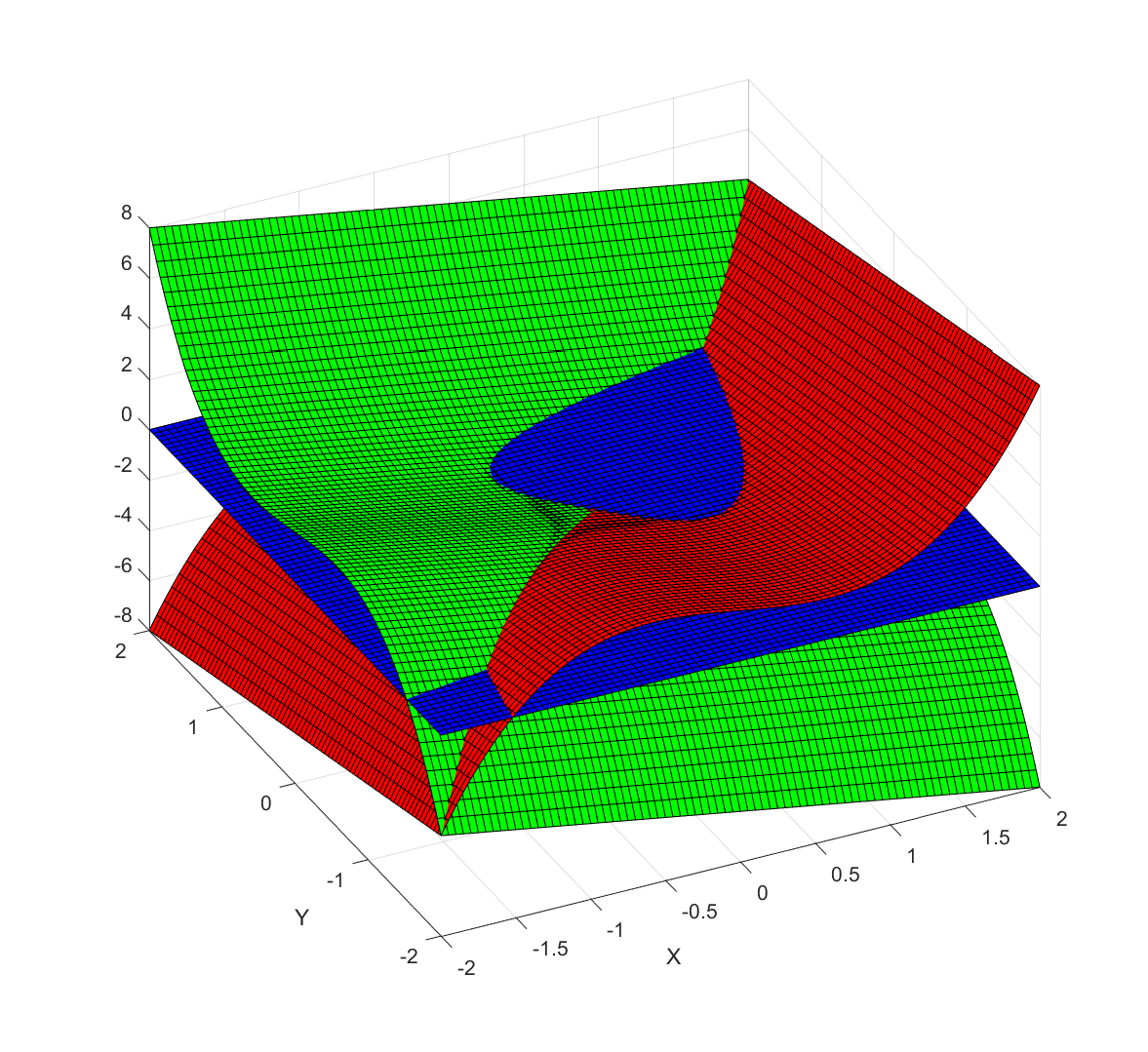
The resulting fractal has a decided modernist bent to it, all hyperbolae and swooshes:
![Behavior of Newton's method in 2D for F=[x^3-x-y, y^3-x-y]. Color denotes value of x+y, with darkening for slow convergence.](http://aleph.se/andart2/wp-content/uploads/2016/12/newton2dp1.png)
Why is the style modernist?
In complex iterations you typically multiply with complex numbers, and if they have an imaginary component (they better have, to be complex!) that introduces a rotation or twist. Hence baroque filaments are ubiquitous, and you get the typical complex “style”.
But here we are essentially multiplying with a real matrix. For a real 2×2 matrix to be a rotation matrix it has to have a pair of imaginary eigenvalues, and for it to at least twist things around the trace needs to be small enough compared to the determinant so that there are complex eigenvalues: (where
and
if the matrix has the usual
form). So if the trace and determinant are randomly chosen, we should expect a majority of cases to be non-rotational.
Moreover, in this particular case, the Jacobian tends to be diagonally dominant (quadratic terms on the diagonal) and that makes the inverse diagonally dominant too: the trace will be big, and hence the chance of seeing rotation goes down even more. The two “knots” where a lot of basins of attraction come together are the points where the trace does vanish, but since the Jacobian is also symmetric there will not be any rotation anyway. Double guarantee.
Can we make a twisty real Newton fractal? If we start with a vanilla rotation matrix and try to find a function that produces it the simplest case is . This is of course just a rotation by the angle theta, and it does not have very interesting zeros.
To get something fractal we need more zeros, and a few zeros in the derivatives too (why? because they cause iterates to be thrown away far from where they were, ensuring a complicated structure of the basin boundaries). One attempt is
. The result is fun, but still far from baroque:


The problem might be that the twistiness is not changing. So we can make to make the dynamics even more complex:

Quite lovely, although still not exactly what I wanted (sounds like a Christmas present).
Back to the classics?
It might be easier just to hide the complex dynamics in an apparently real function like (which produces the archetypal
Newton fractal).
![Newton fractal for F=[x^3-3xy^2-1, 3x^2y-y^3].](http://aleph.se/andart2/wp-content/uploads/2016/12/newtonpert0.png)
, then for
we get:

As we make the function more perturbed, it turns more modernist, undergoing a topological crisis for epsilon between 3.5 and 4:




In the end, we can see that the border between classic baroque complex fractals and the modernist swooshy real fractals is fuzzy. Or, indeed, fractal.