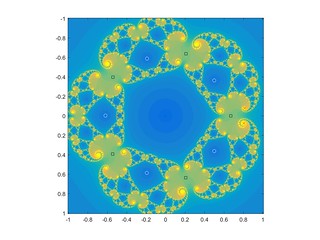
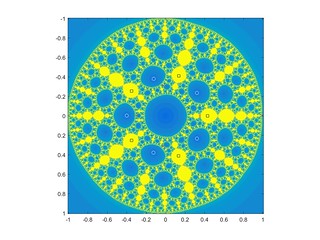
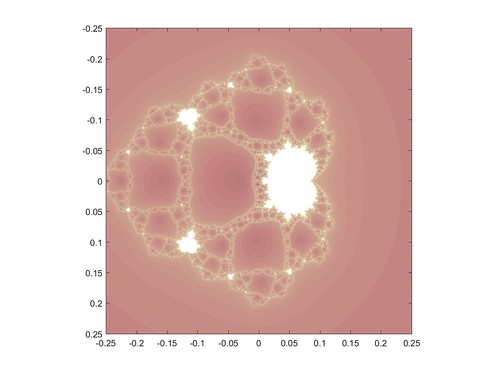
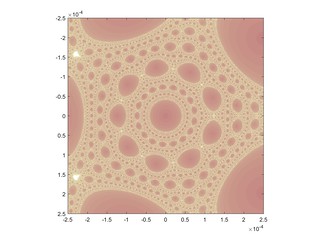
While surfing the web I came across a neat Julia set, defined by iterating for some complex constant c. Here are some typical pictures, and two animations: one moving around a circle in the c-plane, one moving slowly down from c=1 to c=0.

 

The points behind the set

What is going on?

The first step in analysing fractals like this is to find the fixed points and their preimages. is clearly mapped to itself. The term will tend to make large magnitude iterates approach infinity, so it is an attractive fixed point.

is a preimage of infinity: iterates falling on zero will be mapped onto infinity. Nearby points will also end up attracted to infinity, so we have a basin of attraction to infinity around the origin. Preimages of the origin will be mapped to infinity in two steps: has the solutions – this is where the pentagonal symmetry comes from, since these five points are symmetric. Their preimages and so on will also be mapped to infinity, so we have a hierarchy of basins of attraction sending points away forming some gasket-like structure. The Julia set consists of the points that never gets mapped away, the boundary of this hierarchy of basins.

The other fixed points are defined by , which can be rearranged into . They don’t have any neat expression and actually do not affect the big picture dynamics as much. The main reason seems to be that they are unstable. However, their location and the derivative close to them affect the shapes in the Julia set as we will see. Their preimages will be surrounded by the same structures (scaled and rotated) as they have.

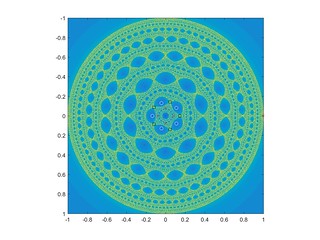
Below are examples with preimages of zero marked as white circles, fixed points as red crosses, and critical points as black squares.

The set behind the points

A simple way of mapping the dynamics is to look at the (generalized) Mandelbrot set for the function, taking a suitable starting point and mapping out its fate in the c-plane. Why that particular point? Because it is one of the critical point where , and a theorem by Julia and Fatou tells us that its fate indicates whether the Julia set is filled or dust-like: bounded orbits of the critical points of a map imply a connected Julia set. When c is in the Mandelbrot set the Julia image has “thick” regions with finite area that do not escape to infinity. When c is outside, then most points end up at infinity, and what remains is either dust or a thin gasket with no area.

The set is much smaller than the vanilla Mandelbrot, with a cuspy main body surrounded by a net reminiscent of the gaskets in the Julia set. It also has satellite vanilla Mandelbrots, which is not surprising at all: the square term tends to dominate in many locations. As one zooms into the region near the origin a long spar covered in Mandelbrot sets runs towards the origin, surrounded by lacework.

One surprising thing is that the spar does not reach the origin – it stops at . Looking at the dynamics, above this point the iterates of the critical point jump around in the interval [0,1], forming a typical Feigenbaum cascade of period doubling as you go out along the spar (just like on the spar of the vanilla Mandelbrot set). But at this location points now are mapped outside the interval, running off to infinity: one of the critical points breaches a basin boundary, causing iterates to run off and the earlier separate basins to merge. Below this point the dynamics is almost completely dominated by the squaring, turning the Julia set into a product of a Cantor set and a circle (a bit wobbly for higher c; it is all very similar to KAM torii). The empty spaces correspond to the regions where preimages of zero throw points to infinity, while along the wobbly circles points get their argument angles multiplied by two for every iteration by the dominant quadratic term: they are basically shift maps. For c=0 it is just the filled unit disk.

So when we allow c to move around a circle as in the animations, the part that passes through the Mandelbrot set has thick regions that thin as we approach the edge of the set. Since the edge is highly convoluted the passage can be quite complex (especially if the circle is “tangent” to it) and the regions undergo complex twisting and implosions/explosions. During the rest of the orbit the preimages just quietly rotate, forming a fractal gasket. A gasket that sometimes looks like a model of the hyperbolic plane, since each preimage has five other preimages, naturally forming an exponential hierarchy that has to be squeezed into a finite roughly circular space.