A question came up on Physics Stack Exchange: how does thrown object trajectories look on a toroidal planet?
Locally we should expect them to be like on Earth: there is constant gravitational acceleration orthogonal to the ground, so they will just look like parabolas.
But if the trajectory is longer the rapid rotation ought to twist it, since there is a fair Coriolis effect. So the differential equation will be If we just look at the velocity vector we get
That is, the forcefield will twist the velocity around if it is large and orthogonal to the angular velocity vector. If the velocity is parallel it will just be affected by gravity. For a trajectory near the pole it will become twisted and tilted:
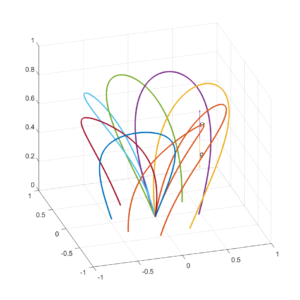
For a starting point on the equator the twisting gets a bit more complex:
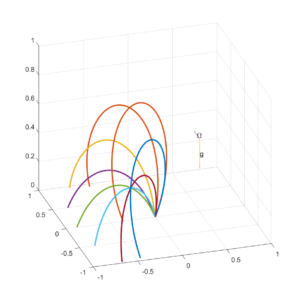
One can also recognise the analogy to an electron in an electromagnetic field: $latex \mathbf{v}’ = (q/m)(\mathbf{E}+\mathbf{v}\times \mathbf{B})$. Without gravity we should hence expect thrown balls to just follow helices around the omega-vector direction just like charged particles follow magnetic field-lines. One can eliminate the electric field from the equation by using a different velocity coordinate $latex \mathbf{v_2}=\mathbf{v}-\mathbf{E}\times\mathbf{B}/B^2$. Hence we can treat ball trajectories like helices plus a drift velocity in the direction. The helix radius will be
.
How large is the Coriolis effect? On Earth . On Donut it is 0.000614 and on Hoop 0.000494, several times higher. Still, the correction is not going to be enormous: for a ball moving 10 meters per second the helix radius will be 69 km on Earth (at the pole), 8.1 km on Donut, and 10 km on Hoop. We hence need to throw the ball a suborbital distance before the twists become really visible. At these distances the curvature of the planet and the non-linearity of the gravitational field also begins to bite.
I have not simulated such trajectories since I need a proper mass distribution model of the worlds, and it is messy. However, for an infinitely thin ring one can solve orbits numerically relatively easily (you “just” have to integrate elliptic integrals):
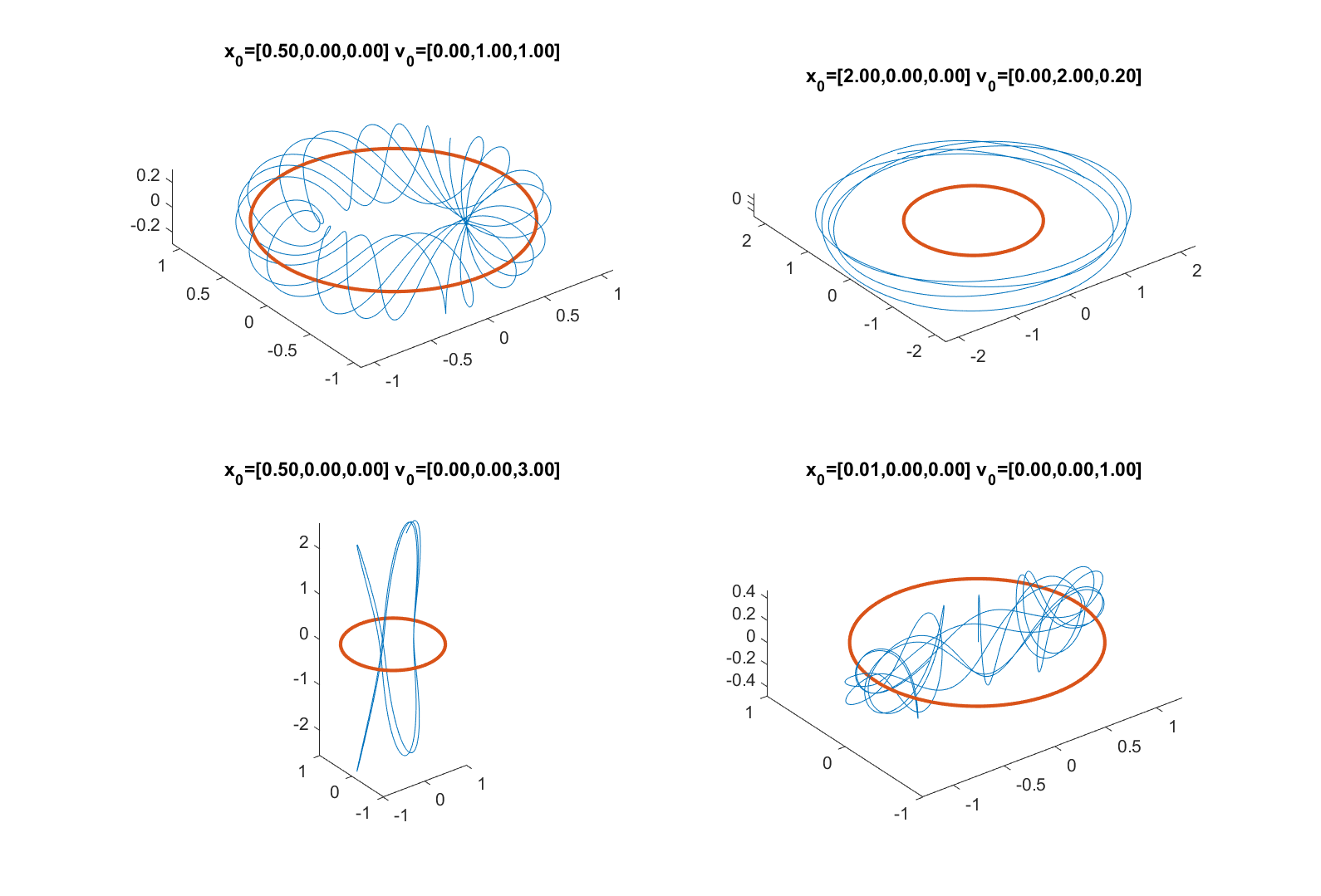
Beside the “normal” equatorial orbits and torus-like orbits winding themselves around the ring, there are internal halo-orbits and chaotic tangles.