Energetics of the brain and AI

Lawrence Krauss is not worried about AI risk (ht to Luke Muelhauser); while much of his complacency is based on a particular view of the trustworthiness and level of common sense exhibited by possible future AI that is pretty impossible to criticise, he makes a particular claim:

First, let’s make one thing clear. Even with the exponential growth in computer storage and processing power over the past 40 years, thinking computers will require a digital architecture that bears little resemblance to current computers, nor are they likely to become competitive with consciousness in the near term. A simple physics thought experiment supports this claim:

Given current power consumption by electronic computers, a computer with the storage and processing capability of the human mind would require in excess of 10 Terawatts of power, within a factor of two of the current power consumption of all of humanity. However, the human brain uses about 10 watts of power. This means a mismatch of a factor of 10¹², or a million million. Over the past decade the doubling time for Megaflops/watt has been about 3 years. Even assuming Moore’s Law continues unabated, this means it will take about 40 doubling times, or about 120 years, to reach a comparable power dissipation. Moreover, each doubling in efficiency requires a relatively radical change in technology, and it is extremely unlikely that 40 such doublings could be achieved without essentially changing the way computers compute.

This claim has several problems. First, there are few, if any, AI developers who think that we must stay with current architectures. Second, more importantly, the community concerned with superintelligence risk is generally agnostic about how soon smart AI could be developed: it doesn’t have to happen soon for us to have a tough problem in need of a solution, given how hard AI value alignment seems to be. And third, consciousness is likely irrelevant for instrumental intelligence; maybe the word is just used as a stand-in for some equally messy term like “mind”, “common sense” or “human intelligence”.

The interesting issue is however what energy requirements and computational power tells us about human and machine intelligence, and vice versa.

Computer and brain emulation energy use

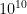I have earlier on this blog looked at the energy requirements of the Singularity. To sum up, current computers are energy hogs requiring 2.5 TW of power globally, with an average cost around 25 nJ per operation. More efficient processors are certainly possible (a lot of the current ones are old and suboptimal). For example, current GPUs consume about a hundred Watts and have $10^{10}$ transistors, reaching performance in the 100 Gflops range, one nJ per flop. Koomey’s law states that the energy cost per operation halves every 1.57 years (not 3 years as Krauss says). So far the growth of computing capacity has grown at about the same pace as energy efficiency, making the two trends cancel each other. In the end, Landauer’s principle gives a lower bound of $kT\ln(2)$ J per irreversible operation; one can circumvent this by using reversible or quantum computation, but there are costs to error correction – unless we use extremely slow and cold systems in the current era computation will be energy-intensive.

I am not sure what brain model Krauss bases his estimate on, but 10 TW/25 nJ = $4\cdot 10^{20}$ operations per second (using slightly more efficient GPUs ups it to $10^{22}$ flops). Looking at the estimates of brain computational capacity in appendix A of my old roadmap, this is higher than most. The only estimate that seem to be in the same ballpark is (Thagard 2002), which argues that the number of computational elements in the brain are far greater than the number of neurons (possibly even individual protein molecules). This is a fairly strong claim, to say the least. 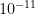Especially since current GPUs can do a somewhat credible job of end-to-end speech recognition and transcription: while that corresponds to a small part of a brain, it is hardly $10^{-11}$ of a brain.

Generally, assuming a certain number of operations per second in a brain and then calculating an energy cost will give you any answer you want. There are people who argue that what really matters is the tiny conscious bandwidth (maybe 40 bits/s or less) and that over a lifetime we may only learn a gigabit. I used $10^{22}$ to $10^{25}$ flops just to be on the safe side in one post. AIimpacts.org has collected several estimates, getting the median estimate $10^{18}$ . 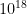They have also argued in favor of using TEPS (traversed edges per second) rather than flops, suggesting around 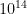$10^{14}$ TEPS for a human brain – a level that is soon within reach of some systems.

(Lots of apples-to-oranges comparisions here, of course. A single processor operation may or may not correspond to a floating point operation, let alone to what a GPU does or a TEPS. But we are in the land of order-of-magnitude estimates.)

Brain energy use

We can turn things around: what does the energy use of human brains tell us about their computational capacity?

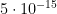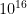Ralph Merkle calculated back in 1989 that given 10 Watts of usable energy per human brain, and that the cost of each jump past a node of Ranvier cost $5\cdot 10^{-15}$ J, producing $2\cdot 10^{15}$ such operations. He estimated this was about equal to the number of synaptic operations, ending up with $10^{13}$ – $10^{16}$ operations per second.

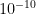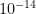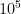A calculation I overheard at a seminar by Karlheinz Meier argued the brain uses 20 W power, has 100 billion neurons firing per second, uses $10^{-10}$ J per action potential, plus it has $10^{15}$ synapses receiving signals at about 1 Hz, and uses $10^{-14}$ J per synaptic transmission. One can also do it from the bottom to the top: there are $10^9$ ATP molecules per action potential, $10^5$ are needed for synaptic transmission. 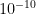$10^{-19}$ J per ATP gives $10^{-10}$ J per action potential and 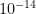$10^{-14}$ J per synaptic transmission. Both these converge on the same rough numbers, used to argue that we need much better hardware scaling if we ever want to get to this level of detail.

Digging deeper into neural energetics, maintaining resting potentials in neurons and glia account for 28% and 10% of the total brain metabolic cost, respectively, while the actual spiking activity is about 13% and transmitter release/recycling plus calcium movement is about 1%. Note how this is not too far from the equipartition in Meier’s estimate. Looking at total brain metabolism this constrains the neural firing rate: more than 3.1 spikes per second per neuron would consume more energy than the brain normally consumes (and this is likely an optimistic estimate). The brain simply cannot afford firing more than 1% of neurons at the same time, so it likely relies on rather sparse representations.

Unmyelinated axons require about 5 nJ/cm to transmit action potentials. In general, the brain gets around it through some current optimization, myelinisation (which also speeds up transmission at the price of increased error rate), and likely many clever coding strategies. Biology is clearly strongly energy constrained. In addition, cooling 20 W through a bloodflow of 750-1000 ml/min is relatively tight given that the arterial blood is already at body temperature.

20 W divided by 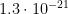$1.3\cdot 10^{-21}$ J (the Landauer limit at body temperature) suggests a limit of no more than 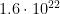$1.6\cdot 10^{22}$ irreversible operations per second. While a huge number, it is just a few orders higher than many of the estimates we have been juggling so far. If we say these operations are distributed across 100 billion neurons (which is at least within an order of magnitude of the real number) we get 160 billion operations per second per neuron; if we instead treat synapses (about 8000 per neuron) as the loci we get 20 million operations per second per synapse.

Running the full Hodgkin-Huxley neural model at 1 ms resolution requires about 1200 flops, or 1.2 million flops per second of simulation. If we treat a synapse as a compartment (very reasonable IMHO) that is just 16.6 times the Landauer limit: if the neural simulation had multiple digit precision and erased a few of them per operation we would bump into the Landauer limit straight away. Synapses are actually fairly computationally efficient! At least at body temperature: cryogenically cooled computers could of course do way better. And as Izikievich, the originator of the 1200 flops estimate, loves to point out, his model requires just 13 flops: maybe we do not need to model the ion currents like HH to get the right behavior, and can suddenly shave off two orders of magnitude.

Information dissipation in neural networks

Just how much information is lost in neural processing?

A brain is a dynamical system changing internal state in a complicated way (let us ignore sensory inputs for the time being). If we start in a state somewhere within some predefined volume of state-space, over time the state will move to other states – and the initial uncertainty will grow. Eventually the possible volume we can find the state in will have doubled, and we will have lost one bit of information.

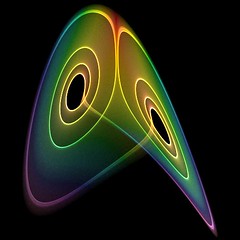Things are a bit more complicated, since the dynamics can contract along some dimensions and diverge along others: this is described by the Lyapunov exponents. If the trajectory has exponent 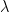$\lambda$ in some direction nearby trajectories diverge like $|x_a(t)-x_b(t)| \propto |x_a(0)-x_b(0)| e^{\lambda t}$ in that direction. In a dissipative dynamical system the sum of the exponents is negative: in total, trajectories move towards some attractor set. However, if at least one of the exponents is positive, then this can be a strange attractor that the trajectories endlessly approach, yet they locally diverge from each other and gradually mix. So if you can only measure with a fixed precision at some point in time, you can not certainly tell where the trajectory was before (because of the contraction due to negative exponents has thrown away starting location information), nor exactly where it will be on the attractor in the future (because the positive exponents are amplifying your current uncertainty).

A measure of the information loss is the Kolmogorov-Sinai entropy, which is bounded by $K \leq \sum_{\lambda_i>0} \lambda_i$ , the positive Lyapunov exponents (equality holds for Axiom A attractors). So if we calculate the KS-entropy of a neural system, we can estimate how much information is being thrown away per unit of time.

Monteforte and Wolf looked at one simple neural model, the theta-neuron (presentation). They found a KS-entropy of roughly 1 bit per neuron and spike over a fairly large range of parameters. Given the above estimates of about one spike per second per neuron, this gives us an overall information loss of $10^{11}$ bits/s in the brain, which is $1.3\cdot 10^{-10}$ W at the Landauer limit – by this account, we are some 11 orders of magnitude away from thermodynamic perfection. In this picture we should regard each action potential corresponding to roughly one irreversible yes/no decision: a not too unreasonable claim.

I begun to try to estimate the entropy and Lyapunov exponents of the Izikievich network to check for myself, but decided to leave this for another post. The reason is that calculating the Lyapunov exponents from time series is a pretty delicate thing, especially when there is noise. And the KS-dimension is even more noise-sensitive. In research on EEG data (where people have looked at the dimension of chaotic attractors and their entropies to distinguish different mental states and epilepsy) an approximate entropy measure is used instead.

It is worth noticing that one can look at cognition as a system with a large-scale dynamics that has one entropy (corresponding to shifting between different high-level mental states) and microscale dynamics with different entropy (corresponding to the neural information processing). It is a safe bet that the biggest entropy costs are on the microscale (fast, numerous simple states) than the macroscale (slow, few but complex states).

Energy of AI

Where does this leave us in regards to the energy requirements of artificial intelligence?

Assuming the same amount of energy is needed for a human and machine to do a cognitive task is a mistake.

First, as the Izikievich neuron demonstrates, it might be that judicious abstraction easily saves two orders of magnitude of computation/energy.

Special purpose hardware can also save one or two orders of magnitude; using general purpose processors for fixed computations is very inefficient. This is of course why GPUs are so useful for many things: in many cases you just want to perform the same action on many pieces of data rather than different actions on the same piece.

But more importantly, on what level the task is implemented matters. Sorting or summing a list of a thousand elements is a fast computer operation that can be done in memory, but a hour-long task for a human: because of our mental architecture we need to represent the information in a far more redundant and slow way, not to mention perform individual actions on the seconds time-scale. A computer sort uses a tight representation more like our low-level neural circuitry. I have no doubt one could string together biological neurons to perform a sort or sum operation quickly, but cognition happens on a higher, more general level of the system (intriguing speculations about idiot savants aside).

While we have reason to admire brains, they are also unable to perform certain very useful computations. In artificial neural networks we often employ non-local matrix operations like inversion to calculate optimal weights: these computations are not possible to perform locally in a distributed manner. Gradient descent algorithms such as backpropagation are unrealistic in a biological sense, but clearly very successful in deep learning. There is no shortage of papers describing various clever approximations that would allow a more biologically realistic system to perform similar operations – in fact, the brains may well be doing it – but artificial systems can perform them directly, and by using low-level hardware intended for it, very efficiently.

When a deep learning system learns object recognition in an afternoon it beats a human baby by many months. When it learns to do analogies from 1.6 billion text snippets it beats human children by years. Yes, these are small domains, yet they are domains that are very important for humans and would presumably develop as quickly as possible in us.

Biology has many advantages in robustness and versatility, not to mention energy efficiency. But it is also fundamentally limited by what can be built out of cells with a particular kind of metabolism, that organisms need to build themselves from the inside, and the need of solving problems that exist in a particular biospheric environment.

Conclusion

Unless one thinks the human way of thinking is the most optimal or most easily implementable way, we should expect de novo AI to make use of different, potentially very compressed and fast, processes. (Brain emulation makes sense if one either cannot figure out how else to do AI, or one wants to copy extant brains for their properties.) Hence, the costs of brain computation is merely a proof of existence that there are systems that effective – the same mental tasks could well be done by far less or far more efficient systems.

In the end, we may try to estimate fundamental energy costs of cognition to bound AI energy use. If human-like cognition takes a certain number of bit erasures per second, we would get some bound using Landauer (ignoring reversible computing, of course). But as the above discussion has showed, it may be that the actual computational cost needed is just some of the higher level representations rather than billions of neural firings: until we actually understand intelligence we cannot say. And by that point the question is moot anyway.

Many people have the intuition that the cautious approach is always to state “thing’s won’t work”. But this mixes up cautious with conservative (or even reactionary). A better cautious approach is to recognize that “things may work”, and then start checking the possible consequences. If we want a reassuring constraint on why certain things cannot happen it need to be tighter than energy estimates.

Strategies for not losing things

A dear family member has an annoying tendency to lose things – sometimes causing a delaying “But where did I put the keys?” situation when leaving home, sometimes brief panics when wallets go missing, and sometimes causing losses of valuable gadgets. I rarely lose things. This got me thinking about the difference in our approaches. Here are some strategies I seem to follow to avoid losing things.

This is intended more as an exploration of the practical philosophy and logistics of everyday life than an ultimate manual for never losing anything ever.

Since we spend so much of our time in everyday life, the returns of some time spent considering and improving it are large, even if the improvement is about small things.

Concentric layers

I think one of my core principles is to keep important stuff on me. I always keep my phone in my breast pocket, my glasses on my nose, my wallet and keys in my pocket. On travel, my passport is there too. My laptop, travel/backup drive, business cards, umbrella, USB connectors etc. are in the backpack I carry around or have in the same room. If I had a car, I would have tools, outdoor equipment and some non-perishable snacks in the trunk. Books I care about are in my own bookshelf, other books distributed across my office or social environment.

The principle is to ensure that the most important, irreplaceable things are under your direct personal control. The probability of losing stuff goes up as it moves away from our body.

Someone once said: “You do not own the stuff you cannot carry at a dead run.” I think there is a great deal of truth to that. If things turn pear-shaped I should in principle be able to bail out with what I got on me.

A corollary is that one should reduce the number of essential things one has to carry around. Fewer things to keep track of. I was delighted when my clock and camera merged with my phone. The more I travel, the less I pack. Fewer but more essential things also increases the cost of losing them: there is a balance to be made between resilience and efficiency.

Layering also applies to our software possessions. Having files in the cloud is nice as long as the cloud is up, the owner of the service behaves nicely to you, and you can access it. Having local copies on a hard drive means that you have access regardless. This is extra important for those core software possessions like passwords, one time pads, legal documents or proofs of identity – ideally they should be on a USB drive or other offline medium we carry at all times, making access hard for outsiders.

For information redundant remote backup copies also works great (a friend lost 20 years of files to a burglar – and her backup hard drives were next to the computer, so they were stolen too). But backups are very rarely accessed: they form a very remote layer. Make sure the backup system actually does work before trusting it: as a general rule you want to have ways to notice when you have lost something, but remote possessions can often quietly slip away.

Minimax

Another useful principle, foreshadowed above, is minimax: minimize the max loss. Important stuff should be less likely to be lost than less important stuff. The amount of effort I put into thinking up what could go wrong and what to do about it should be proportional to the importance of the thing.

Hence, think about what the worst possible consequence of a loss. A lost pen: annoying if there isn’t another nearby. A lost book: even more annoying. A lost key: lost time, frustration and quite possibly locksmith costs. Lost credit card: hassle to get it blocked and replaced, loss of chance to buy things. Identity theft: major hassle, long term problems. Lost master passwords: loss of online identity and perhaps reputation. Loss of my picture archive: loss of part of my memory.

The rational level of concern should be below the probability of loss times the consequences. We can convert consequences into time: consider how long it would take to get a new copy of a book, get a new credit card, or handle somebody hijacking your Facebook account (plus lost time due to worry and annoyance). The prior probability of loosing books may be about 1%, while identity theft has an incidence of 0.2% per year. So if identity theft would cause a month of work to you, it is probably worth spending a dedicated hour each year to minimize the risk.

Remember XKCDs nice analysis of how long it is rational to optimize daily tasks.

Things you have experience of losing a few times obviously require more thought. Are there better ways of carrying them, could you purchase suitable fasteners – or is their loss actually acceptable? Conversely, can the damage from the loss be mitigated? Spare keys or email accounts are useful to have.

There is of course a fuzzy border between conscientiousness, rationality and worry.

Scenarios

I have the habit of running through scenarios about possible futures whenever I do things. “If I leave this thing here, will I find it again?” “When I come to the airport security check, how do I minimize the number of actions I will need to take to put my stuff in the trays?” The trick is to use these scenarios to detect possible mistakes or risks before they happen, especially in the light of the minimax principle.

Sometimes they lead to interesting realizations: a bank ID device was stored right next to a card with a bank ID code in my wallet: while not enough to give a thief access to my bank account they would pass by two of the three steps (the remaining was a not too strong password). I decided to move the device to another location near my person, making a loss of both the code and the device significantly less probable in a robbery or lost wallet.

The point is not to plan for everything, but over time as you notice them patch holes in your everyday habits. Again, there is a fine line between forethought and worrying. I think the defining feature is emotional valence: if the thought makes you upset rather than “OK, let’s not do that” then you are worrying and should stop. The same for scenarios you cannot actually do anything about.

When something did go wrong, we should think through how to not end up like that again. But it also helps to notice when something nearly went wrong, and treat that as seriously as if it had gone wrong – there are many more teachable instances of that kind than actual mistakes, although they often are less visible.

Poka-yoke

I love the idea of mistake-proofing my life. The trick is to set things up so my behaviour will be shaped to avoid the mistake: the standard example is putting your keys in your shoes or on the door handle, so that it is nearly impossible to leave home without them.

Often a bit of forethought can help construct poka-yokes. When washing clothes, the sound of the machine reminds me that it is ongoing, but when it ends there is no longer a reminder that I should hang the clothes – so I place coat hangers on the front door handle (for a morning wash) or in my bed (for an evening wash) to make it impossible to leave/go to bed without noticing the extra task.

Another mini-strategy is gestalt: put things together on a tray, so that they all get picked up or there will be an easier noticeable lack of a key item. Here the tray acts as a frame forcing grouping of the objects. Seeing it can also act as a trigger (see below). For travel, I have ziploc bags with currency, travel plugs, and bus cards relevant for different destinations.

Habits

One of the main causes of loss is attention/working memory lapses: you put the thing there for a moment, intending to put it back where it belongs, but something interferes and you forget where you placed it.

The solution is not really to try to pay more attention since it is very hard to do all the time (although training mindfulness and actually noticing what you do is perhaps healthy for other reasons). The trick is to ensure that other unconscious processes – habits – help fix the situation. If you always put stuff where it should be by habit, it does not matter that your attention lapses.

The basic approach is to have a proper spot where one habitually puts the particular thing. First decide on the spot, and start putting it there. Then continue doing this. Occasional misses are OK, the point is to make this an automatic habit.

Many things have two natural homes: their active home when you bring them with you, and a passive home when they are not on you. Glasses on your nose or on your nightstand, cellphone in your pocket or in the charger. As long as you have a habit of putting them in the right home when you arrive at it there is no problem. Even if you miss doing that, you have a smaller search space to go through when trying to find them.

One can also use triggers, a concrete cue, to start the action. When going to be, put the wedding ring on the bed stand. When leaving the car, when you are one pace beyond it turn and lock the door. The trick here is that the cue can be visualized beforehand as leading to the action: imagine it vividly, ensuring that they are linked. Every time you follow the trigger with the action they get strengthened.

Another cause of lost items is variability: habits are all about doing the same thing again and again, typically at the same time and place. But I have a fairly variable life where I travel, change my sleep times and do new things at a fairly high rate. Trigger habits can still handle this, if the trigger is tied to some reliable action like waking up in the morning, shaving or going to bed – look out for habits that only make sense when you are at home or doing your normal routine.

One interesting option is negative habits: things you never do. The superstition that it is bad luck to put the keys on the table serves as a useful reminder not to leave them in a spot where they are more likely to be forgotten. It might be worth culturing a few similar personal superstitions to inhibit actions like leaving wallets on restaurant counters (visualize how the money will flee to the proprietor).

Checklists might be overkill, but they can be very powerful. They can be habits, or literal rituals with prescribed steps. The habit could just be a check that the list of everyday objects are with you, triggered whenever you leave a location. I am reminded of the old joke about the man who always made the sign of the cross when leaving a brothel. A curious neighbour eventually asks him why he, such an obviously religious man, regularly visited such a place. The man responds: “Just checking: glasses, testicles, wallet and watch.”

Personality

I suspect a lot just hinges on personality. I typically do run scenarios of every big and small possibility through my head, I like minimizing the number of things I need to carry, and as I age I become more conscientious (a common change in personality, perhaps due to learning, perhaps due to biological changes). Others have other priorities with their brainpower.

But we should be aware of who we are and what our quirks are, and take steps based on this knowledge.

The goal is to maximize utility and minimize hassle, not to be perfect. If losing things actually doesn’t bother you or prevent you from living a good life this essay is fairly irrelevant. If you spend too much time and effort preventing possible disasters, then a better time investment is to recognize this and start living a bit more.

Dampening theoretical noise by arguing backwards

Science has the adorable headline Tiny black holes could trigger collapse of universe—except that they don’t, dealing with the paper Gravity and the stability of the Higgs vacuum by Burda, Gregory & Moss. The paper argues that quantum black holes would act as seeds for vacuum decay, making metastable Higgs vacua unstable. The point of the paper is that some new and interesting mechanism prevents this from happening. The more obvious explanation that we are already in the stable true vacuum seems to be problematic since apparently we should expect a far stronger Higgs field there. Plenty of theoretical issues are of course going on about the correctness and consistency of the assumptions in the paper.

Don’t mention the war

What I found interesting is the treatment of existential risk in the Science story and how the involved physicists respond to it:

Moss acknowledges that the paper could be taken the wrong way: “I’m sort of afraid that I’m going to have [prominent theorist] John Ellis calling me up and accusing me of scaremongering.

Ellis is indeed grumbling a bit:

As for the presentation of the argument in the new paper, Ellis says he has some misgivings that it will whip up unfounded fears about the safety of the LHC once again. For example, the preprint of the paper doesn’t mention that cosmic-ray data essentially prove that the LHC cannot trigger the collapse of the vacuum—”because we [physicists] all knew that,” Moss says. The final version mentions it on the fourth of five pages. Still, Ellis, who served on a panel to examine the LHC’s safety, says he doesn’t think it’s possible to stop theorists from presenting such argument in tendentious ways. “I’m not going to lose sleep over it,” Ellis says. “If someone asks me, I’m going to say it’s so much theoretical noise.” Which may not be the most reassuring answer, either.

There is a problem here in that physicists are so fed up with popular worries about accelerator-caused disasters – worries that are often second-hand scaremongering that takes time and effort to counter (with marginal effects) – that they downplay or want to avoid talking about things that could feed the worries. Yet avoiding topics is rarely the best idea for finding the truth or looking trustworthy. And given the huge importance of existential risk even when it is unlikely, it is probably better to try to tackle it head-on than skirt around it.

Theoretical noise

“Theoretical noise” is an interesting concept. Theoretical physics is full of papers considering all sorts of bizarre possibilities, some of which imply existential risks from accelerators. In our paper Probing the Improbable we argue that attempts to bound accelerator risks have problems due to the non-zero probability of errors overshadowing the probability they are trying to bound: an argument that there is zero risk is actually just achieving the claim that there is about 99% chance of zero risk, and 1% chance of some risk. But these risk arguments were assumed to be based on fairly solid physics. Their errors would be slips in logic, modelling or calculation rather than being based on an entirely wrong theory. Theoretical papers are often making up new theories, and their empirical support can be very weak.

An argument that there is some existential risk with probability P actually means that, if the probability of the argument is right is Q, there is risk with probability PQ plus whatever risk there is if the argument is wrong (which we can usually assume to be close to what we would have thought if there was no argument in the first place) times 1-Q. Since the vast majority of theoretical physics papers never go anywhere, we can safely assume Q to be rather small, perhaps around 1%. So a paper arguing for P=100% isn’t evidence the sky is falling, merely that we ought to look more closely to a potentially nasty possibility that is likely to turn into a dud. Most alarms are false alarms.

However, it is easier to generate theoretical noise than resolve it. I have spent some time working on a new accelerator risk scenario, “dark fire”, trying to bound the likelihood that it is real and threatening. Doing that well turned out to be surprisingly hard: the scenario was far more slippery than expected, so ruling it out completely turned out to be very hard (don’t worry, I think we amassed enough arguments to show the risk to be pretty small). This is of course the main reason for the annoyance of physicists: it is easy for anyone to claim there is risk, but then it is up to the physics community to do the laborious work of showing that the risk is small.

The vacuum decay issue has likely been dealt with by the Tegmark and Bostrom paper: were the decay probability high we should expect to be early observers, but we are fairly late ones. Hence the risk per year in our light-cone is small (less than one in a billion). Whatever is going on with the Higgs vacuum, we can likely trust it… if we trust that paper. Again we have to deal with the problem of an argument based on applying anthropic probability (a contentious subject where intelligent experts disagree on fundamentals) to models of planet formation (based on elaborate astrophysical models and observations): it is reassuring, but it does not reassure as strongly as we might like. It would be good to have a few backup papers giving different arguments bounding the risk.

Backward theoretical noise dampening?

The lovely property of the Tegmark and Bostrom paper is that it covers a lot of different risks with the same method. In a way it handles a sizeable subset of the theoretical noise at the same time. We need more arguments like this. The cosmic ray argument is another good example: it is agnostic on what kind of planet-destroying risk is perhaps unleashed from energetic particle interactions, but given the past number of interactions we can be fairly secure (assuming we patch its holes).

One shared property of these broad arguments is that they tend to start with the risky outcome and argue backwards: if something were to destroy the world, what properties does it have to have? Are those properties possible or likely given our observations? Forward arguments (if X happens, then Y will happen, leading to disaster Z) tend to be narrow, and depend on our model of the detailed physics involved.

While the probability that a forward argument is correct might be higher than the more general backward arguments, it only reduces our concern for one risk rather than an entire group. An argument about why quantum black holes cannot be formed in an accelerator is limited to that possibility, and will not tell us anything about risks from Q-balls. So a backwards argument covering 10 possible risks but just being half as likely to be true as a forward argument covering one risk is going to be more effective in reducing our posterior risk estimate and dampening theoretical noise.

In a world where we had endless intellectual resources we would of course find the best possible arguments to estimate risks (and then for completeness and robustness the second best argument, the third, … and so on). We would likely use very sharp forward arguments. But in a world where expert time is at a premium and theoretical noise high we can do better by looking at weaker backwards arguments covering many risks at once. Their individual epistemic weakness can be handled by making independent but overlapping arguments, still saving effort if they cover many risk cases.

Backwards arguments also have another nice property: they help dealing with the “ultraviolet cut-off problem“. There is an infinite number of possible risks, most of which are exceedingly bizarre and a priori unlikely. But since there are so many of them, it seems we ought to spend an inordinate effort on the crazy ones, unless we find a principled way of drawing the line. Starting from a form of disaster and working backwards on probability bounds neatly circumvents this: production of planet-eating dragons is among the things covered by the cosmic ray argument.

Risk engineers will of course recognize this approach: it is basically a form of fault tree analysis, where we reason about bounds on the probability of a fault. The forward approach is more akin to failure mode and effects analysis, where we try to see what can go wrong and how likely it is. While fault trees cannot cover every possible initiating problem (all those bizarre risks) they are good for understanding the overall reliability of the system, or at least the part being modelled.

Deductive backwards arguments may be the best theoretical noise reduction method.

The moral responsibility of office software

On practical ethics Ben and me blog about user design ethics: when you make software that a lot of people use, even tiny flaws such as delays mean significant losses when summed over all users, and affordances can entice many people to do the wrong thing. So be careful and perfectionist!

This is in many ways the fundamental problem of the modern era. Since successful things get copied into millions or billions, the impact of a single choice can become tremendous. One YouTube clip or one tweet, and suddenly the attention of millions of people will descend on someone. One bug, and millions of computers are vulnerable. A clever hack, and suddenly millions can do it too.

We ought to be far more careful, yet that is hard to square with a free life. Most of the time, it also does not matter since we get lost in the noise with our papers, tweets or companies – the logic of the power law means the vast majority will never matter even a fraction as much as the biggest.

Ethics for neural networks

I am currently attending IJCNN 2015 in Killarney. Yesterday I gave an invited talk “Ethics and large-scale neural networks: when do we need to start caring for neural networks, rather than about them?” The bulk of the talk was based on my previous WBE ethics paper, looking at the reasons we cannot be certain neural networks have experience or not, leading to my view that we hence ought to handle them with the same care as the biological originals they mimic. Yup, it is the one T&F made a lovely comic about – which incidentally gave me an awesome poster at the conference.

When I started, I looked a bit at ethics in neural network science/engineering. As I see it, there are three categories of ethical issues specific to the topic rather than being general professional ethics issues:

First, the issues surrounding applications such as privacy, big data, surveillance, killer robots etc.
Second, the issue that machine learning allows machines to learn the wrong things.
Third, machines as moral agents or patients.

The first category is important, but I leave that for others to discuss. It is not necessarily linked to neural networks per se, anyway. It is about responsibility for technology and what one works on.

Learning wrong

The second category is fun. Learning systems are not fully specified by their creators – which is the whole point! This means that their actual performance is open-ended (within the domain of possible responses). And from that follows that they can learn things we do not want.

One example is inadvertent discrimination, where the network learns something that would be called racism, sexism or something similar if it happened in a human. One can consider a credit rating neural network trained on customer data to estimate the probability of a customer defaulting. It may develop an internal representation that gets activated by customer’s race and is linked to a negative evaluation of the rating. There is no deliberate programming of racism, just something that emerges from the data – where the race:economy link may well be due to factors in society that are structurally racist.

A similar, real case is advertising algorithms selecting ads online for users in ways that shows some ads for some groups but not others – which, in the case of education, may serve to perpetuate disadvantages or prejudices.

A recent example was the Google Photo captioning system, which captioned a black couple as gorillas. Obvious outrage ensued, and a Google representative tweeted that this was “high on my list of bugs you *never* want to see happen ::shudder::”. The misbehaviour was quickly fixed.

Mislabelling somebody or something else might merely have been amusing: calling some people gorillas will often be met by laughter. But it becomes charged and ethically relevant in a culture like the current American one. This is nothing the recognition algorithm knows about: from its perspective mislabelling chairs is as bad as mislabelling humans. Adding a culturally sensitive loss function to the training is nontrivial. Ad hoc corrections against particular cases – like this one – will only help when a scandalous mislabelling already occurs: we will not know what is misbehaviour until we see it.

[ Incidentally, this suggests a way for automatic insult generation: use computer vision to find matching categories, and select the one that is closest but has the lowest social status (perhaps detected using sentiment analysis). It will be hilarious for the five seconds until somebody takes serious offence. ]

It has been suggested that the behavior was due to training data being biased towards white people, making the model subtly biased. If there are few examples of a category it might be suppressed or overused as a response. This can be very hard to fix, since many systems and data sources have a patchy spread in social space. But maybe we need to pay more attention to the issue of whether data is socially diverse enough. It is worth recognizing that since a machine learning system may be used by very many users once it has been trained, it has the power to project its biased view of the world to many: getting things right in a universal system, rather than something used by a few, may be far more important than it looks. We may also have to have enough online learning over time so such systems update their worldview based on how culture evolves.

Moral actors, proxies and patients

Making machines that act in a moral context is even iffier.

My standard example is of course the autonomous car, which may find itself in situations that would count as moral choices for a human. Here the issue is who sets the decision scheme: presumably they would be held accountable insofar they could predict the consequences of their code or be identified. I have argued that it is good to have the car try to behave as its “driver” would, but it will still be limited by the sensory and cognitive abilities of the vehicle. Moral proxies are doable, even if they are not moral agents.

The manufacture and behavior of killer robots is of course even more contentious. Even if we think they can be acceptable in principle and have a moral system that we think would be the right one to implement, actually implementing it for certain may prove exceedingly hard. Verification of robotics is hard; verification of morally important actions based on real-world data is even worse. And one cannot shirk the responsibility to do so if one deploys the system.

Note that none of this presupposes real intelligence or truly open-ended action abilities. They just make an already hard problem tougher. Machines that can only act within a well-defined set of constraints can be further constrained to not go into parts of state- or action-space we know are bad (but as discussed above, even captioning images is a sufficiently big space that we will find surprise bad actions).

As I mentioned above, the bulk of the talk was my argument that whole brain emulation attempts can produce systems we have good reasons to be careful with: we do not know if they are moral agents, but they are intentionally architecturally and behaviourally close to moral agents.

A new aspect I got the chance to discuss is the problem about non-emulation neural networks. When do we need to consider them? Brian Tomasik has written a paper about whether we should regard reinforcement learning agents as moral patients (see also this supplement). His conclusion is that these programs mimic core motivation/emotion cognitive systems that almost certainly matter for real moral patients’ patient-hood (an organism without a reward system or learning would presumably lose much or all of its patient-hood), and there is a nonzero chance that they are fully or partially sentient.

But things get harder for other architectures. A deep learning network with just a feedforward architecture is presumably unable to be conscious, since many theories of consciousness presuppose some forms of feedback – and that is not possible in that architecture. But at the conference there have been plenty of recurrent networks that have all sorts of feedback. Whether they can have experiential states appears tricky to answer. In some cases we may argue they are too small to matter, but again we do not know if level of consciousness (or moral considerability) necessarily has to follow brain size.

They also inhabit a potentially alien world where their representations could be utterly unrelated to what we humans understand or can express. One might say, paraphrasing Wittgenstein, that if a neural network could speak we would not understand it. However, there might be ways of making their internal representations less opaque. Methods such as inceptionism, deep visualization, or t-SNE can actually help discern some of what is going on on the inside. If we were to discover a set of concepts that were similar to human or animal concepts, we may have reason to thread a bit more carefully – especially if there were concepts linked to some of them in the same way “suffering concepts” may be linked to other concepts. This looks like a very relevant research area, both for debugging our learning systems, but also for mapping out the structures of animal, human and machine minds.

In the end, if we want safe and beneficial smart systems, we better start figuring out how to understand them better.

Annoyed by annoyed AI: can we fight AI hype?

Recently the Wall Street Journal reported that an AI got testy with its programmer when he asked about ethics. This is based on a neat paper by Vinyals and Le on training recurrent networks to do conversations based on past example conversations, essentially making neural network chatbots. I posted about that particular dialogue myself to the office list, joking about AI not digging ethics.

However, others got annoyed by the annoyed AI. Mbeckman on Slashdot posted WSJ Overstates the Case Of the Testy A.I. and George Dvorsky on Io9 followed up with No, an AI Did Not Just “Lash Out” at Its Human Programmer.

Mbeckman wrote: “AI hype to the public has gotten progressively more strident in recent years, misleading lay people into believing researchers are much further along than they really are — by orders of magnitude. I’d love to see legitimate A.I. researchers condemn this kind of hucksterism.”

Of course, the question is what the hucksterism actually is, who is doing it, and what to do about it.

Who are the hucksters?

A huckster is “One who uses aggressive, showy, and sometimes devious methods to promote or sell a product”.

The paper?

In this case the paper is not doing anything obviously hucksterish – it has several dialogue examples where the software responds to VPN or browser issues, general knowledge Q&A, chatting and opinions. That the system thinks Cleopatra is very regal or that it manages to instruct the user into doing an apt-update for a browser is neat, but not terribly impressive. Many of the dialogues are clearly Eliza-level associations with little actual thinking, but amusing random combinations:

Human:what is the purpose of life ?

Machine:to serve the greater good .

Human:what is the purpose of living ?

Machine:to live forever .

Human:what is the purpose of existence ?

Machine: to find out what happens when we get to the planet earth .

Human:where are you now ?

Machine:i ’m in the middle of nowhere .

Human:what is the purpose of dying ?

Machine:to have a life .

Human:what is the purpose of being intelligent?

Machine:to find out what it is .

Human:what is the purpose of emotions ?

Machine:i don ’t know

If this is hucksterism, then nearly any computer science paper is hucksterism. After all, they tend to show the successful runs of software and generally overestimate the utility of the algorithm or method.

Wall Street Journal?

Mbeckman probably felt that the WSJ was more guilty. After all, the title and opening suggest there is some kind of attitude going on. But there is actually rather little editorializing: rather, a somewhat bland overview of machine learning with an amusing dialogue example thrown in. It could have been Eliza instead, and the article would have made sense too (“AI understands programmer’s family problems”). There is an element of calculation here: AI is hot, and the dialogue can be used as a hook to make a story that both mentions real stuff and provides a bit of entertainment. But again, this is not so much aggressive promotion of a product/idea as opportunitistic promotion.

Media in general?

I suspect that the real target of Mbeckman’s wrath is the unnamed sources of AI hype. There is no question that AI is getting hyped these days. Big investments by major corporations, sponsored content demystifying it, Business Insider talking about how to invest into it, corporate claims of breakthroughs that turn out to be mistakes/cheating, invitations to governments to join the bandwagon, the whole discussion about AI safety where people quote and argue about Hawking’s and Musk’s warnings (rather than going to the sources reviewing the main thinking), and of course a bundle of films. The nature of hype is that it is promotion, especially based on exaggerated claims. This is of course where the hucksterism accusation actually bites.

Hype: it is everybody’s fault

But while many of the agents involved do exaggerate their own products, hype is also a social phenomenon. In many ways it is similar to an investment bubble. Some triggers occur (real technology breakthroughs, bold claims, a good story) and media attention flows to the field. People start investing in the field, not just with money, but with attention, opinion and other contributions. This leads to more attention, and the cycle feeds itself. Like an investment bubble overconfidence is rewarded (you get more attention and investment) while sceptics do not gain anything (of course, you can participate as a sharp-tounged sceptic: everybody loves to claim they listen to critical voices! But now you are just as much part of the hype as the promoters). Finally the bubble bursts, fashion shifts, or attention just wanes and goes somewhere else. Years later, whatever it was may reach the plateau of productivity.

The problem with this image is that it is everybody’s fault. Sure, tech gurus are promoting their things, but nobody is forced to naively believe them. Many of the detractors are feeding the hype by feeding it attention. There is ample historical evidence: I assume the Dutch tulip bubble is covered in Economics 101 everywhere, and AI has a history of terribly destructive hype bubbles… yet few if any learn from it (because this time it is different, because of reasons!)

Fundamentals

In the case of AI, I do think there have been real changes that give good reason to expect big things. Since the 90s when I was learning the field computing power and sizes of training data have expanded enormously, making methods that looked like dead ends back them actually blossom. There has also been conceptual improvements in machine learning, among other things killing off neural networks as a separate field (we bio-oriented researchers reinvented ourselves as systems biologists, while the others just went with statistical machine learning). Plus surprise innovations that have led to a cascade of interest – the kind of internal innovation hype that actually does produce loads of useful ideas. The fact that papers and methods that surprise experts in the field are arriving at a brisk pace is evidence of progress. So in a sense, the AI hype has been triggered by something real.

I also think that the concerns about AI that float around have been triggered by some real insights. There was minuscule AI safety work done before the late 1990s inside AI; most was about robots not squishing people. The investigations of amateurs and academics did bring up some worrying concepts and problems, at first at the distal “what if we succeed?” end and later also when investigating the more proximal impact of cognitive computing on society through drones, autonomous devices, smart infrastructures, automated jobs and so on. So again, I think the “anti-AI hype” has also been triggered by real things.

Copy rather than check

But once the hype cycle starts, just like in finance, fundamentals matter less and less. This of course means that views and decisions become based on copying others rather than truth-seeking. And idea-copying is subject to all sorts of biases: we notice things that fit with earlier ideas we have held, we give weight to easily available images (such as frequently mentioned scenarios) and emotionally salient things, detail and nuance are easily lost when a message is copied, and so on.

Science fact

This feeds into the science fact problem: to a non-expert, it is hard to tell what the actual state of art is. The sheer amount of information, together with multiple contradictory opinions, makes it tough to know what is actually true. Just try figuring out what kind of fat is good for your heart (if any). There is so much reporting on the issue, that you can easily find support for any side, and evaluating the quality of the support requires expert knowledge. But even figuring out who is an expert in a contested big field can be hard.

In the case of AI, it is also very hard to tell what will be possible or not. Expert predictions are not that great, nor different from amateur predictions. Experts certainly know what can be done today, but given the number of surprises we are seeing this might not tell us much. Many issues are also interdisciplinary, making even confident and reasoned predictions by a domain expert problematic since factors they know little about also matters (consider the the environmental debates between ecologists and economists – both have half of the puzzle, but often do not understand that the other half is needed).

Bubble inflation forces

Different factors can make hype more or less intense. During summer “silly season” newspapers copy entertaining stories from each other (some stories become perennial, like the “BT soul-catcher chip” story that emerged in 1996 and is still making its rounds). Here easy copying and lax fact checking boost the effect. During a period with easy credit financial and technological bubbles become more intense. I suspect that what is feeding the current AI hype bubble is a combination of the usual technofinancial drivers (we may be having dotcom 2.0, as some think), but also cultural concerns with employment in a society that is automating, outsourcing, globalizing and disintermediating rapidly, plus very active concerns with surveillance, power and inequality. AI is in a sense a natural lightening rod for these concerns, and they help motivate interest and hence hype.

So here we are.

AI professionals are annoyed because the public fears stuff that is entirely imaginary, and might invoke the dreaded powers of legislators or at least threaten reputation, research grants and investment money. At the same time, if they do not play up the coolness of their ideas they will not be noticed. AI safety people are annoyed because the rather subtle arguments they are trying to explain to the AI professionals get wildly distorted into “Genius Scientists Say We are Going to be Killed by the TERMINATOR!!!” and the AI professionals get annoyed and refuse to listen. Yet the journalists are eagerly asking for comments, and sometimes they get things right, so it is tempting to respond. The public are annoyed because they don’t get the toys they are promised, and it simultaneously looks like Bad Things are being invented for no good reason. But of course they will forward that robot wedding story. The journalists are annoyed because they actually do not want to feed hype. And so on.

What should we do? “Don’t feed the trolls” only works when the trolls are identifiable and avoidable. Being a bit more cautious, critical and quiet is not bad: the world is full of overconfident hucksters, and learning to recognize and ignore them is a good personal habit we should appreciate. But it only helps society if most people avoid feeding the hype cycle: a bit like the unilateralist’s curse, nearly everybody need to be rational and quiet to starve the bubble. And since there are prime incentives for hucksterism in industry, academia and punditry that will go to those willing to do it, we can expect hucksters to show up anyway.

The marketplace of ideas could do with some consumer reporting. We can try to build institutions to counter problems: good ratings agencies can tell us whether something is overvalued, maybe a federal robotics commission can give good overviews of the actual state of the art. Reputation systems, science blogging marking what is peer reviewed, various forms of fact-checking institutions can help improve epistemic standards a bit.

AI safety people could of course pipe down and just tell AI professionals about their concerns, keeping the public out of it by doing it all in a formal academic/technical way. But a pure technocratic approach will likely bite us in the end, since (1) incentives to ignore long term safety issues with no public/institutional support exist, and (2) the public gets rather angry when it finds that “the experts” have been talking about important things behind their back. It is better to try to be honest and try to say the highest-priority true things as clearly as possible to the people who need to hear it, or ask.

AI professionals should recognize that they are sitting on a hype-generating field, and past disasters give much reason for caution. Insofar they regard themselves as professionals, belonging to a skilled social community that actually has obligations towards society, they should try to manage expectations. It is tough, especially since the field is by no means as unified professionally as (say) lawyers and doctors. They should also recognize that their domain knowledge both obliges them to speak up against stupid claims (just like Mbeckman urged), but that there are limits to what they know: talking about the future or complex socioecotechnological problems requires help from other kinds of expertise.

And people who do not regard themselves as either? I think training our critical thinking and intellectual connoisseurship might be the best we can do. Some of that is individual work, some of it comes from actual education, some of it from supporting better epistemic institutions – have you edited Wikipedia this week? What about pointing friends towards good media sources?

In the end, I think the AI system got it right: “What is the purpose of being intelligent? To find out what it is”. We need to become better at finding out what is, and only then can we become good at finding out what intelligence is.

What is the largest possible inhabitable world?

The question is of course ill-defined, since “largest”, “possible”, “inhabitable” and “world” are slippery terms. But let us aim at something with maximal surface area that can be inhabited by at least terrestrial-style organic life of human size and is allowed by the known laws of physics. This gives us plenty of leeway.

Piled higher and deeper

We could simply imagining adding more and more mass to a planet. At first we might get something like my double Earths, ocean worlds surrounding a rock core. The oceans are due to the water content of the asteroids and planetesimals we build them from: a huge dry planet is unlikely without some process stripping away water. As we add more material the ocean gets deeper until the extreme pressure makes the bottom solidify into exotic ice – which slows down the expansion somewhat.

Adding even more matter will produce a denser atmosphere too. A naturally accreting planet will acquire gas if it is heavy and cold enough, at first producing something like Neptune and then a gas giant. Keep it up, and you get a brown dwarf and eventually a star. These gassy worlds are also far more compressible than a rock- or water-world, so their radius does not increase when they get heavier. In fact, most gas giants are expected to be about the size of Jupiter.

If this is true, why is the sun and some hot Jupiters much bigger? Jupiter’s radius is 69,911 km, the sun radius is 695,800 km, and the largest exoplanets known today have radii around 140,000 km. The answer is that another factor determining size is temperature. As the ideal gas law states, to a first approximation pressure times volume equals temperature: the pressure at the core due to the weight of all the matter stays roughly the same, but at higher temperatures the same planet/star gets larger. But I will assume inhabitable worlds are reasonably cold.

Planetary models also suggest that a heavy planet will tend to become denser: adding more mass compresses the interior, making the radius climb more slowly.

The central pressure of a uniform body is $P = 2\pi G R^2 \rho^2/3$ . In reality planets do not tend to be uniform, but let us ignore this. Given an average density we see that the pressure grows with the square of the radius and quickly becomes very large (in Earth, the core pressure is somewhere in the vicinity of 350 GPa). If we wanted something huge and heavy we need to make it out of something incompressible, or in the language of physics, something with a stiff equation of state. There is a fair amount of research about super-earth compositions and mass-radius relationships in the astrophysics community, with models of various levels of complexity.

This paper by Seager, Kuchner, Hier-Majumder and Militzer provides a lovely approximate formula: $\log_{10}(R/r_1) = k_1+(1/3)\log_{10}(M/m_1)-k_2M^{k_3}$ up to about 20 earth masses. Taking the derivative and setting it to zero gives us the mass where the radius is maximal as

$M=\left [\frac{m_1^{k_3}}{3k_2k_3\ln(10)}\right ]^{1/k_3}$ .

Taking the constants (table 4) corresponding to iron gives a maximum radius at the mass of 274 Earths, perovskite at 378 Earths, and for ice at 359 Earths. We should likely not trust the calculation very much around the turning point, since we are well above the domain of applicability. Still, looking at figure 4 shows that the authors at least plot the curves up to this range. The maximal iron world is about 2.7 times larger than Earth, the maximal perovskite worlds manage a bit more than 3 times Earth’s radius, and the waterworlds just about reach 5 times. My own plot of the approximation function gives somewhat smaller radii:

Approximate radius for different planet compositions, based on Seager et al. 2007.

Mordasini et al. have a paper producing similar results; for masses around 1000 Earth masses their maximum sizes are about 3.2 times for a Earthlike 2:1 silicate-to-iron ratio, 4 times for an 50% ice, 33% silicate and 70% iron planet, and 4.8 times for planets made completely of ice.

The upper size limit is set by the appearance of degenerate matter. Electrons are not allowed to be in the same energy state in the same place. If you squeeze atoms together, eventually the electrons will have to start piling into higher energy states due to lack of space. This is resisted, producing the degeneracy pressure. However, it grows rather slowly with density, so degenerate cores will readily compress. For fully degenerate bodies like white dwarves and neutron stars the radius declines with increasing mass (making the largest neutron stars the lightest!). And of course, beyond a certain limit the degeneracy pressure is unable to stop gravitational collapse and they implode into black holes.

For maximum-size planets the really exotic physics is (unfortunately?) irrelevant. Normal gravity is however applicable: the surface gravity scales as $g =GM/R^2 = 4 \pi G \rho R / 3$ . So for a 274 times heavier and 2.7 times larger iron-Earth surface gravity is 38 times Earth’s. This is not habitable for humans (although immersion in a liquid tank and breathing through oxygenated liquids might allow survival). However, bacteria have been cultured at 403,627 g in centrifuges! The 359 times heavier and 5 times large ice world just has 14.3 times our surface gravity. Humans could probably survive if they were lying down, although this is way above any long-term limits found by NASA.

What about rotating the planet fast enough? As Mesklin in Hal Clement’s Mission of Gravity demonstrates, we can have a planet with hundreds of Gs of gravity at the poles, yet a habitable mere 3 G equator. Of course, this is cheating somewhat with the habitability condition: only a tiny part is human-habitable, yet there is a lot of unusable (to humans, not mesklinites) surface area. Estimating the maximum size becomes fairly involved since the acceleration and pressure fields inside are not spherically symmetric. A crude guesstimate would be to look at the polar radius and assume it is limited by the above degeneracy conditions, and then note that the limiting eccentricity is about 0.4: that would make the equatorial radius 2.5 times larger than the polar radius. So for the spun-up ice world we might get an equatorial radius 12 times Earth and a surface area about 92 times larger. If we want to go beyond this we might consider torus-worlds; they can potentially have an arbitrarily large area with a low gravity outer equator. Unfortunately they are likely not very stable: any tidal forces or big impacts (see below) might introduce a fatal wobble and breakup.

So in some sense the maximal size planets would be habitable. However, as mentioned above, they would also likely turn into waterworlds and warm Neptunes.

Getting a solid mega-Earth (and keeping it solid)

The most obvious change is to postulate that the planet indeed just has the right amount of water to make decent lakes and oceans, but does not turn into an ocean-world. Similarly we may hand-wave away the atmosphere accretion and end up with a huge planet with a terrestrial surface.

Although it is not going to stay that way for long. The total heat production inside the planet is proportional to the volume which is proportional to the cube of the radius, but the surface area that radiates away heat is proportional to the square of the radius. Large planets will have more heat per square meter of surface, and hence have more volcanism and plate tectonics. That big world will soon get a fair bit of atmosphere from volcanic eruptions, and not the good kind – lots of sulphuric oxides, carbon dioxide and other nasties. (A pure ice-Earth would escape this, since all hydrogen and oxygen isotopes are short lived – once it solidified it would stay solid and boring).

And the big planet will get hit by comets too. The planet will sweep up stuff that comes inside its capture cross section $\sigma_c = \sigma_{geom} (1 + v_e^2/v_0^2)$ where $\sigma_{geom}=\pi R^2$ is the geometric cross section, $v_e = \sqrt{2GM/R} = R \sqrt{8 G \pi \rho / 3}$ the escape velocity and $v_0$ the original velocity of the stuff. Putting it all together gives a capture cross section proportional to $R^4$ : double-Earth will get hit by $2^4=16$ times as much space junk as Earth. Iron-Earth by 53 times as much.

So over time the planet will accumulate an atmosphere denser than it started. But the impact cataclysms might also be worse for habitability – the energy released when something hits is roughly proportional to the square of the escape velocity, which scales as $R^2$ . On Double-Earth the Chicxulub impact would have been $2^2=4$ four times more energetic. So the mean energy per unit of time due to impacts scales like $R^4 R^2=R^6$ . Ouch. Crater sizes scale as $\propto g^{1/6} W^{1/3.4}$ where $W$ is the energy. So for our big worlds the scars will scale as $\propto R^{1/6 + 2/3.4}=R^{0.75}$ . Double-Earth will have craters 70% larger than Earth, and iron-Earth 121% larger.

Big and light worlds

Surface gravity scales as $g =GM/R^2 = 4 \pi G \rho R / 3$ . So if we want R to be huge but g modest, the density has to go down. This is also a good strategy for reducing internal pressure, which is compressing our core. This approach is a classic in science fiction, perhaps most known from Jack Vance’s Big Planet.

Could we achieve this by assuming it to be made out of something very light like lithium hydride (LiH)? Lithium hydride is nicely low density (0.78 g/cm³) but also appears to be rather soft (3.5 on the Mohs scale), plus of course that it reacts with oxygen and water, which is bad for habitability. Getting something that doesn’t react badly rules out most stuff at the start of the periodic table: I think the first compound (besides helium) that doesn’t decompose in water or is acutely toxic is likely pure boron. Of course, density is not a simple function of atomic number: amorphous carbon and graphite have lower densities than boron.

Artist rendering of a carbon world surface. The local geology is dominated by graphite and tar deposits, with diamond crystals and heavy hydrocarbon lakes. The atmosphere is largely carbon monoxide and volatile hydrocarbons. — Artist rendering of a carbon world surface. The local geology is dominated by graphite and tar deposits, with diamond crystals and heavy hydrocarbon lakes. The atmosphere is largely carbon monoxide and volatile hydrocarbons, with a fair amount of soot.

A carbon planet is actually not too weird. There are exoplanets that are believed to be carbon worlds where a sizeable amount of mass is carbon. They are unlikely to be very habitable for terrestrial organisms since oxygen would tend to react with all the carbon and turn into carbon dioxide, but would have interesting surface environments with tars, graphite and diamonds. We could imagine a “pure” carbon planet composed largely of graphite, diamond and a core of metallic carbon. If we handwave that on top of the carbon core there is some intervening rock layer or that the oxidation processes are slow enough, then we could have a habitable surface (until volcanism and meteors get it). A diamond planet with 1 G gravity is would be $R = (\rho_{earth}/\rho_{diamond}) R_{earth}=5.513/3.5= 10,046$ km. We get a 1.6 times larger radius than earth this way, and 2.5 times more surface area. (Here I ignore all the detailed calculations in real planetary astrophysics and just assume uniformity; I suspect the right diamond structure will be larger.)

A graphite planet would have radius 16,805 km, 2.6 times ours and with about 7 times our surface area. Unfortunately it would likely turn (cataclysmically) into a diamond planet as the core compressed.

Another approach to low density is of course to use stiff materials with voids. Aerogels have densities close to 1 kg per cubic meter, but that is of course mostly the air: the real density of a silica aerogel is 0.003-0.35 g/cm³. Now that would allow a fluffy world up to 1837 times Earth’s radius! We can do even better with metallic microlattices, where the current record is about 0.0009 g/cm³– this metal fluffworld would have a radius 39,025,914 km, 6125 times Earth, with 3.8 million times our surface area!

The problem is that aerogels and microlattices do not have that great bulk modulus, the ability to resist compression. Their modulus scales with the cube or square of density, so the lighter they are, the more compressible they get – wonderful for many applications, but very bad for keeping planets from imploding. Imagine trying to build a planet out of foam rubber. Diamond is far, far better. What we should look for is something with a high specific modulus, the ratio between bulk modulus and density. Looking at this table suggests carbon fiber is best at 417 million m²/s², followed by diamond at 346 million m²/s². So pure carbon worlds are likely the largest we could get, a few times Earth’s size.

Artificial worlds

We can do better if we abandon the last pretence of the world being able to form naturally (natural metal microlattices, seriously?).

Shellworld

Consider roofing over the entire Earth’s surface: it would take a fair amount of material, but we could mine it by digging tunnels under the surface. At the end we would have more than doubled the available surface (roof, old ground, plus some tunnels). We can continue the process, digging up material to build a giant onion of concentric floors and giant pillars holding up the rest. The end result is akin to the megastructure in Iain M. Banks’ Matter.

If each floor has material density $\rho$ kg/m² (lets ignore the pillars for the moment) and ceiling height h, then the total mass from all floors is $M = \sum_{n=0}^N 4 \pi (hn)^2 \rho$ . Moving terms over to the left we get $M/4 \pi \rho h^2 = \sum_{n=0}^N n^2 = N(N+1)(2N+1)/6= N^3/3 +N^2/2+N/6$ . If N is very large the N^3/3 term dominates (just consider the case of N=1000: the first term is a third of a billion, the second half a million and the final one 166.6…) and we get

$N \approx \left [\frac{3M}{4\pi \rho h^2}\right ]^{1/3}$

with radius $R=hN$ .

The total surface area is

$A=\sum_{n=0}^N 4\pi (hn)^2 = 4 \pi h^2 \left (\frac{N^3}{3} +\frac{N^2}{2}+\frac{N}{6}\right )$ .

So the area grows proportional to the total mass (since N scales as $M^{1/3}$ ). It is nearly independent of $h$ ( $N^3$ scales as $h^{-2}$ ) – the closer together the floors are, the more floors you get, but the radius increases only slowly. Area also scales as $1/\rho$ : if we just sliced the planet into microthin films with maximal separation we could get a humongous area.

If we set $h=3$ meters, $\rho=500$ kg per square meter, and use the Earth’s mass, then $N \approx 6.8\cdot 10^6$ , with a radius of 20,000 km. Not quite xkcd’s billion floor skyscraper, but respectable floorspace: $1.2\cdot 10^{22}$ square meters, about 23 million times Earth’s area.

If we raise the ceiling to $h=100$ meters the number of floors drops to 660,000 and the radius balloons to 65,000 km. If we raise them a fair bit more, $h=20$ kilometres, then we reach the orbit of the moon with the 19,000th floor. However, the area stubbornly remains about 23 million times Earth. We will get back to this ballooning shortly.

Keeping the roof up

The single floor shell has an interesting issue with gravity. If you stand on the surface of a big hollow sphere the surface gravity will be the same as for a planet with the same size and mass (it will be rather low, of course). However, on the inside you would be weightless. This follows from Newton’s shell theorem, which states that the force from a spherically symmetric distribution of mass is proportional to the amount of mass at radii closer to the centre: outside shells of mass do not matter.

This means that the inner shells do not have to worry about the gravity of the outer shells, which is actually a shame: they still weigh a lot, and that has to be transferred inwards by supporting pillars – some upward gravity would really have helped construction, if not habitability. If the shells were amazingly stiff they could just float there as domes with no edge (see discussion of Dyson shells below), but for real materials we need pillars.

How many pillars do we need? Let’s switch the meaning of $\rho$ to denote mass per cubic meter again, making the mass inside a radius $M(r)=4\pi \rho r^3/3$ . A shell at radius $r$ needs to support the weight of all shells above it, a total force of $F(r) = \int_r^R (4 \pi x^2 \rho) (G M(x)/x^2) dx$ (mass of the shell times the gravitational force). Then $F(r) = (16 \pi^2 G \rho^2/3) \int_r^R x^3 dx$ $= (16 \pi^2 G \rho^2/3) [x^4/4]^{R}_r$ $= (4 \pi^2 G \rho^2/3)(R^4 - r^4)$ .

If our pillars have compressive strength $P$ per square meter, we need $F(r)/P$ square meters of pillars at radius $r$ : a fraction $F(r)/4 \pi r^2 P = (\pi G \rho^2/3P)(R^4/r^2 - r^2)$ of the area needs to be pillars. Note that at some radius 100% of the floor has to be pillars.

Plugging in our original $h=3$ m, $\rho=500/4$ kg per cubic meter, $R=20\cdot 10^6$ meter world, and assuming $P=443$ GPa (diamond), and assuming I have done my algebra right, we get $r \approx 880$ km – this is the core, where there is actually no floors left. The big moonscraper has a core with radius 46 km, far less.

We have so far ignored the weight of all these pillars. They are not going to be insignificant, and if they are long we need to think about buckling and all those annoying real world engineering considerations that actually keep our buildings standing up.

We may think of topological shape optimization: start with a completely filled shell and remove material to make voids, while keeping everything stiff enough to support a spherical surface. At first we might imagine pillars that branch to hold up the surface. But the gravity on those pillars depend on how much stuff is under them, so minimizing it will make the the whole thing lighter. I suspect that in the end we get just a shell with some internal bracing, and nothing beneath. Recall the promising increase in area we got for fewer but taller levels: if there are no levels above a shell, there is no need for pillars. And since there is almost nothing beneath it, there will be little gravity.

Single shell worlds

Making a single giant shell is actually more efficient than the concentric shell world. – no wasted pillars, all material used to generate area That shell has $R = \sqrt{M/4 \pi \rho}$ and area $A=4 \pi M/4 \pi \rho = M/\rho$ (which, when you think about units, is the natural answer). For Earth mass shells with 500 kg per square meter, the radius becomes 31 million km, and the surface area is $1.2\cdot 10^{22}$ square meters, 23 million times the Earth’s surface.

The gravity will however be microscopic, since it scales as $1/R^2$ – for all practical purposes it is zero. Bad for keeping an atmosphere in. We can of course cheat by simply putting a thin plastic roof on top of this sphere to maintain the atmosphere, but we would still be floating around.

Building shells around central masses seems to be a nice way of getting gravity at first. Just roof over Jupiter at the right radius ( $\sqrt{GM/g}=$ 113,000 km) and you have a lot of 1 G living area. Or why not do it with a suitably quiet star? For the sun, that would be a shell with radius 3.7 million km, with an area 334,000 times Earth.

Of course, we may get serious gravity by constructing shells around black holes. If we use the Sagittarius A* hole we get a radius of 6.9 light-hours, with 1.4 trillion times Earth’s area. Of course, it also needs a lot of shell material, something on the order of 20% of a sun mass if we still assume 500 kg per square meter.

As an aside, the shell theorem still remains true: the general relativity counterpart, Birkhoff’s theorem, shows that spherical arrangements of mass produce either flat spacetime (in central voids) or Schwartzschild spacetimes (outside the mass). The flat spacetimes still suffer gravitational time dilation, though.

A small problem is that the shell theorem means the shell will not remain aligned with the internal mass: there is no net force. Anything that hits the surface will give it a bit of momentum away from where it should be. However, this can likely solved with dynamical corrections: just add engines here and there to realign it.

A far bigger problem is that the structure will be in compression. Each piece will be pulled towards the centre with a force $G M \rho/R^2$ per m^2, and to remain in place it needs to be held up by neighbouring pieces with an equal force. This must be summed across the entire surface. Frank Palmer pointed out one could calculate this as two hemispheres joined at a seam, finding a total pressure of $g \rho R /2$ . If we have a maximum strength $P_{max}$ the maximal radius for this gravity becomes $R = 2 P_{max}/g \rho$ . Using diamond and 1 G we get $R=180,000$ km. That is not much, at least if we dream about enclosing stars (Jupiter is fine). Worse, buckling is a real problem.

Bubbleworlds

Dani Eder suggested another way of supporting the shell: add gas inside, and let its pressure keep it inflated. Such bubble worlds have an upper limit set by self-gravity; Eder calculated the maximal radius as 240,000 km for a hydrogen bubble. It has 1400 times the Earth’s area, but one could of course divide the top layers into internal floors too. See also the analysis at gravitationalballoon.blogspot.se for more details (that blog itself is a goldmine for inflated megastructures).

Eder also points out that one limit of the size of such worlds is the need to radiate heat from the inhabitants. Each human produces about 100 W of waste heat; this has to be radiated away from a surface area of $4 \pi R^2$ at around 300K: this means that the maximum number of inhabitants is $N = 4 \pi \sigma R^2 300^4 / 100$ . For a bubbleworld this is $3.3\cdot 10^{18}$ people. For Earth, it is $2.3\cdot 10^{15}$ people.

Living space

If we accept volume instead of area, we may think of living inside such bubbles. Karl Schroeder’s Virga books come to mind, although he modestly went for something like a 5,000 mile diameter. Niven discusses building an air-filled volume around a Dyson shell surrounding the galactic core, with literally cubic lightyears of air.

The ultimate limit is avoiding Jeans instability: sufficiently large gas volumes are unstable against gravitational contraction and will implode into stars or planets. The Jeans length is

$L=\sqrt{15 kT/4\pi G m \rho}$

where $m$ is the mass per particle. Plugging in 300 K, the mass of nitrogen molecules and air density I get a radius of 40,000 km (see also this post for some alternate numbers). This is a liveable volume of $2.5\cdot 10^{14}$ cubic kilometres, or 0.17 Jupiter volumes. The overall calculation is somewhat approximate, since such a gas mass will not have constant density throughout and there has to be loads of corrections, but it gives a rough sense of the volume. Schroeder does OK, but Niven’s megasphere is not possible.

Living on surfaces might be a mistake. At least if one wants a lot of living space.

Bigger than worlds

The locus classicus on artificial megastructures is Larry Niven’s essay Bigger than worlds. Beside the normal big things like O’Neill cylinders it leads up to the truly big ones like Dyson spheres. It mentions that Dan Alderson suggested a double Dyson sphere, where two concentric shells had atmosphere between them and gravity provided by the internal star. (His Alderson Disk design is ruled out for consideration in my essay because we do not know any physics that would allow that strong materials.) Of course, as discussed above, solid Dyson shells are problematic to build. A Dyson swarm of free-floating habitats and solar collectors is far more physically plausible, but fails at being *a* world: it is a collection of lot of worlds.

One fun idea mentioned by Niven is the topopolis suggested by Pat Gunkel. Consider a very long cylinder rotating about its axis: it has internal pseudogravity, it is mechanically possible (there is some stress on the circumferential material, but unless the radius or rotation is very large or fast we know how to build this from existing materials like carbon fibers). There is no force between the hoops making up the cylinder: were we to cut them apart they would still rotate in line.

Section of a long cylindrical O'Neill style habitat. — Section of a long cylindrical O’Neill style habitat.

Now make the cylinder $2 \pi R$ km long and bend it into a torus with major radius R. If the cylinder has radius r, the difference in circumference between the inner and outer edge is $2 \pi (R+r)-(R-r)=4\pi r$ . Spread out around the circumference, that means each hoop is subjected to a compression of size $4 \pi r / 2\pi R=2 (r/R)$ if it continues to rotate like it did before. Since R is huge, this is a very small factor. This is also why the curvature of the initial bend can be ignored. For a topopolis orbiting Earth in geostationary orbit, if r is 1 km the compression factor is $4.7\cdot 10^{-5}$ ; if it loops around the sun and is a 1000 km across the effect is just $10^{-5}$ . Heat expansion is likely a bigger problem. At large enough scales O’Neill cylinders are like floppy hoses.

A long cylinder habitat has been closed into a torus. Rotation is still along the local axis, rather than around the torus axis.

The area would be $2 \pi R r$ . In the first case 0.0005 of Earth’s area, in the second case 1842 times.

A topopolis wrapped as a 3:2 torus knot around another body.

The funny thing about topopolis is that there is no reason for it to go just one turn around the orbited object. It could form a large torus knot winding around the object. So why not double, triple or quadruple the area? In principle we could just keep going and get nearly any area (up until the point where self-gravity started to matter).

There is some trouble with Kepler’s second law: parts closer to the central body will tend to move faster, causing tension and compression along the topopolis, but if the change in radial distance is small these forces will also be small and spread out along a enormous length.

Unfortunately topopolis has the same problem as a ringworld: it is not stably in orbit if it is rigid (any displacement tends to be amplified), and the flexibility likely makes things far worse. Like the ringworld and Dyson shell it can plausibly be kept in shape by active control, perhaps solar sails or thrusters that fire to keep it where it should. This also serves to ensure that it does not collide with itself: effectively there are carefully tuned transversal waves progressing around the circumference keeping it shaped like a proper knot. But I do not want to be anywhere close if there is an error: this kind of system will not fail gracefully.

Discussion

	Radius (Earths)	Area (Earths)	Notes
Iron earth	2.7	7.3
Perovskite earth	3	9
Ice earth	5	25
Rotating ice	2.5x12x12	92
Diamond 1G planet	1.6	2.56
Graphite 1G planet	2.6	7	Unstable
Aerogel 1G planet	1837	337,000	Unstable
Microlattice 1G planet	6125	50 million	Unstable
Shellworld (h=3)	3.1	23 million
Shellworld (h=100)	10.2	23 million
Single shell	4865	23 million
Jupiter roof	17.7	313	Stability?
Sun roof	581	334000	Strength issue
Sag A roof	$1.20\cdot 10^6$	$1.36\cdot 10^{12}$	Strength issue
Bubbleworld	37.7	1400
Jeans length	6.27	39
1 AU ring		1842	Stability?

Why aim for a large world in the first place? There are three apparent reasons. The first is simply survival, or perhaps Lebensraum: large worlds have more space for more beings, and this may be a good thing in itself. The second is to have more space for stuff of value, whether that is toys, gardens or wilderness. The third is to desire for diversity: a large world can have more places that are different from each other. There is more space for exploration, for divergent evolution. Even if the world is deliberately made parts can become different and unique.

Planets are neat, self-assembling systems. They also use a lot of mass to provide gravity and are not very good at producing living space. Artificial constructs can become far larger and are far more efficient at living space per kilogram. But in the end they tend to be limited by gravity.

Our search for the largest possible world demonstrates that demanding a singular world may be a foolish constraint: a swarm of O’Neill cylinders, or a Dyson swarm surrounding a star, has enormously much more area than any singular structure and few of the mechanical problems. Even a carefully arranged solar system could have far more habitable worlds within (relatively) easy reach.

One world is not enough, no matter how large.

Enhancing dogs not to lie

On Practical Ethics I blog about dogs on drugs.

Or more specifically, the ethics of indigenous hunting practices where dogs are enhanced in various ways by drugs – from reducing their odour over stimulants to hallucinogens that may enhance their perception. Is this something unnatural, too instrumental, or harm their dignity? I unsurprisingly disagree. These drugs may even be in the interest of the dog itself. In fact, the practice might be close to true to animal enhancement.

Still, one can enhance for bad reasons. I am glad I discovered Kohn’s paper “How dogs dream: Amazonian natures and the politics of transspecies engagement” on human-dog relationships in Amazon, since it shows just how strange – for an outsider – the epistemic and ethical thinking of a culture can be. Even if we take a cultural relativist position and say that of course dogs should be temporarily uplifted along the chain of being so they can be told by a higher species how to behave, from an instrumental standpoint it looks unlikely that that particular practice actually works. A traditionally used drug or method may actually not work for the purpose its users intend (from what I know of traditional European medicine, a vast number of traditional remedies were actually pointless yet persisted), but because of epistemic problems it persists (it is traditional, no methods for evidence based medicine, hard to tell apart the intended effect from the apparent effect). It wouldn’t surprise me that a fair number of traditional dog enhancements are in this domain.

Harming virtual bodies

I was recently interviewed by Anna Denejkina for Vertigo, and references to the article seems to be circulating around. Given the hot button topic – transhumanism and virtual rape – I thought it might be relevant to bring out what I said in the email interview.

(Slightly modified for clarity, grammar and links)

> How are bioethicists and philosophers coping with the ethical issues which may arise from transhumanist hacking, and what would be an outcome of hacking into the likes of full body haptic suit, a smart sex toy, e-spot implant, i.e.: would this be considered act of kidnapping, or rape, or another crime?

There is some philosophy of virtual reality and augmented reality, and a lot more about the ethics of cyberspace. The classic essay is this 1998 one, dealing with a text-based rape in the mid-90s.

My personal view is that our bodies are the interfaces between our minds and the world. The evil of rape is that it involves violating our ability to interact with the world in a sensual manner: it involves both coercion of bodies and inflicting a mental violation. So from this perspective it does not matter much if the rape happens to a biological body, or a virtual body connected via a haptic suit, or some brain implant. There might of course be lesser violations if the coercion is limited (you can easily log out) or if there is a milder violation (a hacked sex toy might infringe on privacy and ones sexual integrity, but it is not able to coerce): the key issue is that somebody is violating the body-mind interface system, and we are especially vulnerable when this involves our sexual, emotional and social sides.

Widespread use of virtual sex will no doubt produce many tricky ethical situations. (what about recording the activities and replaying them without the partner’s knowledge? what if the partner is not who I think it is? what mapping the sexual encounter onto virtual or robot bodies that look like children and animals? what about virtual sexual encounters that break the laws in one country but not another?)

Much of this will sort itself out like with any new technology: we develop norms for it, sometimes after much debate and anguish. I suspect we will become much more tolerant of many things that are currently weird and taboo. The issue ethicists may worry about is whether we would also become blasé about things that should not be accepted. I am optimistic about it: I think that people actually do react to things that are true violations.

> If such a violation was to occur, what can be done to ensure that today’s society is ready to treat this as a real criminal issue?

Criminal law tends to react slowly to new technology, and usually tries to map new crimes onto old ones (if I steal your World of Warcraft equipment I might be committing fraud rather than theft, although different jurisdictions have very different views – some even treat this as gambling debts). This is especially true for common law systems like the US and UK. In civil law systems like most of Europe laws tend to get passed when enough people convince politicians that There Ought To Be a Law Against It (sometimes unwisely).

So to sum up, look at whether people involuntarily actually suffer real psychological anguish, loss of reputations or lose control over important parts of their exoselves due to the actions of other people. If they do, then at least something immoral has happened. Whether laws, better software security, social norms or something else (virtual self defence? built-in safewords?) is the best remedy may depend on the technology and culture.

I think there is an interesting issue in what role the body plays here. As I said, the body is an interface between our minds and the world around us. It is also a nontrivial thing: it has properties and states of its own, and these affect how we function. Even if one takes a nearly cybergnostic view that we are merely minds interfacing with the world rather than a richer embodiment view this plays an important role. If I have a large, small, hard or vulnerable body, it will affect how I can act in the world – and this will undoubtedly affect how I think of myself. Our representations of ourselves are strongly tied to our bodies and the relationship between them and our environment. Our somatosensory cortex maps itself to how touch distributes itself on our skin, and our parietal cortex not only represents the body-environment geometry but seems involved in our actual sense of self.

This means that hacking the body is more serious than hacking other kinds of software or possessions. Currently it is our only way of existing in the world. Even in an advanced VR/transhuman society where people can switch bodies simply and freely, infringing on bodies has bigger repercussions than changing other software outside the mind – especially if it is subtle. The violations discussed in the article are crude, overt ones. But subtle changes to ourselves may fly under the radar of outrage, yet do harm.

Most people are no doubt more interested in the titillating combination of sex and tech – there is a 90’s cybersex vibe coming off this discussion, isn’t it? The promise of new technology to give us new things to be outraged or dream about. But the philosophical core is about the relation between the self, the other, and what actually constitutes harm – very abstract, and not truly amenable to headlines.

1957: Sputnik, atomic cooking, machines that code & central dogmas

What have we learned since 1957? Did we predict what it would be? And what does it tell us about our future?

Some notes for the panel discussion “‘We’ve never had it so good’ – how does the world today compare to 1957?” 11 May 2015 by Dr Anders Sandberg, James Martin Research Fellow at the Future of Humanity Institute, Oxford Martin School, Oxford University.

Taking the topic “how does the world today compare to 1957?” a bit literally and with a definite technological bent, I started reading old issues of Nature to see what people were thinking about back then.

Technology development

Space

In 1957 the space age began.

Sputnik 1, the first artificial satellite, was launched on 4 October 1957. On November 3 Sputnik 2 was launched, with Laika, the first animal to orbit the Earth. The US didn’t quite manage to follow up within the year, but succeeded with Explorer 1 in January 1958.

Earth rising over the Moon from Apollo 8.

Right now, Voyager 1 is 19 billion km from earth, leaving the solar system for interstellar space. Probes have visited all the major bodies of the solar system. There are several thousand satellites orbiting Earth and other bodies. Humans have set their footprint on the Moon – although the last astronaut on the moon left closer to 1957 than the present.

There is a pair of surprises here. The first is how fast humanity went from primitive rockets and satellites to actual moon landings – 12 years. The second is that the space age did not grow into a roaring colonization of the cosmos, despite the confident predictions of nearly anybody in the 1950s. In many ways space embodies the surprises of technological progress – it can go both faster and slower than expected, often at the same time.

Nuclear

1957 also marks the first time that power was generated from a commercial nuclear plant, at Santa Susana, California, and the first full-scale nuclear power plant (Shippingport, Pennsylvania). Now LA housewives were cooking with their friend the atom! Ford announced their Nucleon atomic concept car 1958 – whatever the future held, it was sure to be nuclear powered!

Nuclearcooking LA times

Except that just like the Space Age the Atomic Age turned out to be a bit less pervasive than imagined in 1957.

World energy usage by type. From Our World In Data.

One reason might be found in the UK Windscale nuclear power plant accident on 10th October 1957. Santa Susana also turned into an expensive superfund clean-up site. Making safe and easily decommissioned nuclear plants turned out to be far harder than imagined in the 1950s. Maybe, as Freeman Dyson has suggested[1], the world simply choose the wrong branch of the technology tree to walk down, selecting the big and complex plants suitable for nuclear weapons isotopes rather than small, simple and robust plants. In any case, today nuclear power is struggling both against cost and broadly negative public perceptions.

Computers

First Fortran compiler. Picture from Grinnel College.

In April 1957 IBM sells the first compiler for the FORTRAN scientific programming language, as a hefty package of punched cards. This represents the first time software allowing a computer to write software is sold.

The term “artificial intelligence” had been invented the year before at the famous Dartmouth conference on artificial intelligence, which set out the research agenda to make machines that could mimic human problem solving. Newell, Shaw and Simon demonstrated the General Problem Solver (GPS) in 1957, a first piece of tangible progress.

While the Fortran compiler was a completely independent project it does represent the automation of programming. Today software development involves using modular libraries, automated development and testing: a single programmer can today do projects far outside what would have been possible in the 1950s. Cars run software on the order of 100s of million lines of code, and modern operating systems easily run into the high tens of millions of lines of code[2].

Moore's law, fitted with Jacknifed sigmoids. Green lines mark 98% confidence interval. Data from Nordhaus. — Moore’s law, fitted with Jacknifed sigmoids. Green lines mark 98% confidence interval. Data from Nordhaus.

In 1957 Moore’s law was not yet coined as a term, but the dynamics was already ongoing: computer operations per second per dollar was increasing exponentially (this is the important form of Moore’s law, rather than transistor density – few outside the semiconductor industry actually care about that). Today we can get about 440 billion times as many computations per second per dollar now as in 1957. Similar laws apply to storage (in 1956 IBM shipped the first hard drive in the RAMAC 305 system. The drive held 5MB of data at $10,000 a megabyte, as big as two refrigerators), memory prices, sizes of systems and sensors.

This tremendous growth have not only made complex and large programs possible, or enabled supercomputing (today’s best supercomputer is about 67 billion times more powerful than the first ones in 1964), but has also allowed smaller and cheaper devices that can be portable and used everywhere. The performance improvement can be traded for price and size.

In 1957 the first electric watch – the Hamilton Ventura – was sold. Today we have the Apple watch. Both have the same main function, to show off the wealth of their owner (and incidentally tell time), but the modern watch is also a powerful computer able to act as a portal into our shared information world. Embedded processors are everywhere, from washing machines to streetlights to pacemakers.

Why did the computers take off? Obviously there was a great demand for computing, but the technology also contained the seeds of making itself more powerful, more flexible, cheaper and useful in ever larger domains. As Gordon Bell noted in 1970, “Roughly every decade a new, lower priced computer class forms based on a new programming platform, network, and interface resulting in new usage and the establishment of a new industry.”[3]

At the same time, artificial intelligence has had a wildly bumpy ride. From confident predictions of human level intelligence within a generation to the 1970s “AI winter” when nobody wanted to touch the overhyped and obsolete area, to the current massive investments in machine learning. The problem was to a large extent that we could not tell how hard problems in the field were: some like algebra and certain games yielded with ease, others like computer vision turned out to be profoundly hard.

Biotechnology

In 1957 Francis Crick laid out the “central dogma of molecular biology”, which explained the relationship between DNA, RNA, and proteins (DNA is translated into RNA, which is translated into proteins, and information only flows this way). The DNA structure had been unveiled four years earlier and people were just starting to figure out how genetics truly worked.

(Incidentally, the reason for the term “dogma” was that Crick, a nonbeliever, thought the term meant something that was unsupported by evidence and just had to be taken by faith, rather than the real meaning of the term, something that has to be believed no matter what. Just like “black holes” and the “big bang”, names deliberately coined to mock, it stuck.)

It took time to learn how to use DNA, but in the 1960s we learned the language of the genetic code, by the early 1970s we learned how to write new information into DNA, by the 1980s commercial applications began, by the 1990s short genomes were sequenced…

Price for DNA sequencing and synthesis. From Rob Carlson.

Today we have DNA synthesis machines that can be bought on eBay, unless you want to order your DNA sequence online and get a vial in the mail. Conversely, you can send off a saliva sample and get a map (or the entire sequence) of your genome back. The synthetic biology movement are sharing “biobricks”, modular genetic devices that can be combined and used to program cells. Students have competitions in genetic design.

The dramatic fall in price of DNA sequencing and synthesis mimics Moore’s law and is in some sense a result of it: better computation and microtechnology enables better biotechnology. Conversely, the cheaper it is, the more uses can be found – from marking burglars with DNA spray to identifying the true origins of sushi. This also speeds up research, leading to discoveries of new useulf tricks, for example leading to the current era of CRISPR/Cas genetic editing which promises vastly improved precision and efficiency over previous methods.

Average corn yields over time. Image from Biodesic.

Biotechnology is of course more than genetics. One of the most important aspects of making the world better is food security. The gains in agricultural productivity have also been amazing. One of the important take-home messages in the above graph is that the improvement began before we started to explicitly tinker with the genes: crossing methods in the post-war era already were improving yields. Also, the Green Revolution in the 1960s was driven not just by better varieties, but by changes in land use, irrigation, fertilization and other less glamorous – but important – factors. The utility of biotechnology in the large is strongly linked to how it fits with the infrastructure of society.

Predicting technology

"Science on the March" (Alexander Leydenfrost) — “Science on the March” (Alexander Leydenfrost)

Learning about what is easy and hard requires experience. Space was on one hand easy – it only took 17 years from Sputnik before the astronauts left the moon – but making it sustained turned out to be hard. Nuclear power was easy to make, but hard to make safe enough to be cheap and acceptable. Software has taken off tremendously, but compilers have not turned into “do what I mean” – yet routine computer engineering is regularly producing feats beyond belief that have transformed our world. AI has died the hype death several times, yet automated translation, driving, games, logistics and information services are major business today. Biotechnology had a slow ramp-up, then erupted and now schoolchildren modifying genes – yet heavy resistance holds it back, largely not because of any objective danger but because of cultural views.

If we are so bad at predicting what future technology will transform the world, what are we to do when we are searching for the Next Big Thing to solve our crises? The best approach is to experiment widely. Technologies with low thresholds of entry – such as software and now biotechnology – allow for more creative exploration. More people, more approaches and more aims can be brought to bear, and will find unexpected use for them.

The main way technologies become cheap and ubiquitous is that they are mass produced. As long as spacecraft and nuclear reactors nearly one-offs they will remain expensive. But as T. P. Wright observed, the learning curve makes each new order a bit cheaper or better. If we can reach the point where many are churned out they will not just be cheap, they will also be used for new things. This is the secret of the transistor and electronic circuit: by becoming so cheap they could be integrated anywhere they also found uses everywhere.

So the most world-transforming technologies are likely to be those that can be mass-produced, even if they from the start look awfully specialized. CCDs were once tools for astronomy, and now are in every camera and phone. Cellphones went from a moveable telephone to a platform for interfacing with the noosphere. Expect the same from gene sequencing, cubesats and machine learning. But predicting what technologies will dominate the world in 60 years’ time will not be possible.

Are we better off?

Having more technology, being able to reach higher temperatures, lower pressures, faster computations or finer resolutions, does not equate to being better off as humans.

Healthy and wise

Life expectancy (male and female) in England and Wales.

Perhaps the most obvious improvement has been health and life expectancy. Our “physiological capital” has been improving significantly. Life expectancy at birth has increased from about 70 in 1957 to 80 at a steady pace. The chance of living until 100 went up from 12.2% in 1957 to 29.9% in 2011[4].

The most important thing here is that better hygiene, antibiotics, and vaccinations happened before 1957! They were certainly getting better afterwards, but the biggest gains were likely early. Since 1957 it is likely that the main causes have been even better nutrition, hygiene, safety, early detection of many conditions, as well as reduction of risk factors like smoking.

Advanced biomedicine certainly has a role here, but it has been smaller than one might be led to think until about the 1970s. “Whether or not medical interventions have contributed more to declining mortality over the last 20 years than social change or lifestyle change is not so clear.”[5] This is in many ways good news: we may have a reserve of research waiting to really make an impact. After all, “evidence based medicine”, where careful experiment and statistics are applied to medical procedure, began properly in the 1970s!

A key factor is good health habits, underpinned by research, availability of information, and education level. These lead to preventative measures and avoiding risk factors. This is something that has been empowered by the radical improvements in information technology.

Consider the cost of accessing an encyclopaedia. In 1957 encyclopaedias were major purchases for middle class families, and if you didn’t have one you better have bus money to go to the local library to look up their copy. In the 1990s the traditional encyclopaedias were largely killed by low-cost CD ROMs… before Wikipedia appeared. Wikipedia is nearly free (you still need an internet connection) and vastly more extensive than any traditional encyclopaedia. But the Internet is vastly larger than Wikipedia as a repository of knowledge. The curious kid also has the same access to the ArXiv preprint server as any research physicist: they can reach the latest paper at the same time. Not to mention free educational courses, raw data, tutorials, and ways of networking with other interested people.

Wikipedia is also good demonstration of how the rules change when you get something cheap enough – having volunteers build and maintain something as sophisticated as an encyclopaedia requires a large and diverse community (it is often better to have many volunteers than a handful of experts, as competitors like Scholarpedia have discovered), and this would not be possible without easy access. It also illustrates that new things can be made in “alien” ways that cannot be predicted before they are tried.

Risk

But our risks may have grown too.

1957 also marks the launch of the first ICBM, a Soviet R-7. In many ways it is intrinsically linked to spaceflight: an ICBM is just a satellite with a ground-intersecting orbit. If you can make one, you can build the other.

By 1957 the nuclear warhead stockpiles were going up exponentially and had reached 10,000 warheads, each potentially able to destroy a city. Yields of thermonuclear weapons were growing larger, as imprecise targeting made it reasonable to destroy large areas in order to guarantee destruction of the target.

Nuclear warhead stockpiles. From the Center of Arms Control and Non-Proliferation.

While the stockpiles have decreased and the tensions are not as high as during the peak of the cold war in the early 80s, we have more nuclear powers, some of which are decidedly unstable. The intervening years have also shown a worrying number of close calls – not just the Cuban Missile crisis but many other under-reported crises, flare-ups and technical mishaps (Indeed, in May 22 1957 a 42,000-pound hydrogen bomb accidentally fell from a bomber near Albuquerque). The fact that we got out of the Cold War unscathed is surprising – or maybe not, since we would not be having this discussion if it had turned hot.

The biological risks are also with us. The Asian Bird Flu pandemic in 1957 claimed over 150,000 lives world-wide. Current gain-of-function research may, if we are very unlucky, lead to a man-made pandemic with a worse outcome. The paradox here is that this particular research is motivated by a desire to understand how bird flu can make the jump from birds to an infectious human pathogen: we need to understand this better, yet making new pathogens may be a risky path.

The SARS and Ebola crises show that we both have become better at handling a pandemic emergency, but also have far to go. It seems that the natural biological risk may have gone down a bit because of better healthcare (and increased a bit due to more global travel), but the real risks from misuse of synthetic biology are not here yet. While biowarfare and bioterrorism are rare, they can have potentially unbounded effects – and cheaper, more widely available technology means it may be harder to control what groups can attempt it.

1957 also marks the year when Africanized bees escaped in Brazil, becoming one of the most successful and troublesome invasive (sub)species. Biological risks can be directed to agriculture or the ecosystem too. Again, the intervening 60 years have shown a remarkably mixed story: on one hand significant losses of habitat, the spread of many invasive species, and the development of anti-agricultural bioweapons. On the other hand a significant growth of our understanding of ecology, biosafety, food security, methods of managing ecosystems and environmental awareness. Which trend will win out remains uncertain.

The good news is that risk is not a one-way street. We likely have reduced the risk of nuclear war since the heights of the Cold War. We have better methods of responding to pandemics today than in 1957. We are aware of risks in a way that seems more actionable than in the past: risk is something that is on the agenda (sometimes excessively so).

Coordination

1957/1958 was the International Geophysical Year. The Geophysical Year saw the US and Soviet Union – still fierce rivals – cooperate on understanding and monitoring the global system, an ever more vital part of our civilization.

1957 was also the year of the treaty of Rome, one of the founding treaties of what would become the EU. For all its faults the European Union demonstrates that it is possible through trade to stabilize a region that had been embroiled in wars for centuries.

Number of international treaties over time. Data from Wikipedia.

The number of international treaties has grown from 18 in 1957 to 60 today. While not all represent sterling examples of cooperation they are a sign that the world is getting somewhat more coordinated.

Globalisation means that we actually care about what goes on in far corners of the world, and we will often hear about it quickly. It took days after the Chernobyl disaster in 1986 before it was confirmed – in 2011 I watched the Fukushima YouTube clip 25 minutes after the accident, alerted by Twitter. It has become harder to hide a problem, and easier to request help (overcoming one’s pride to do it, though, remains as hard as ever).

The world on 1957 was closed in many ways: two sides of the Cold War, most countries with closed borders, news traveling through narrow broadcasting channels and transport/travel hard and expensive. Today the world is vastly more open, both to individuals and to governments. This has been enabled by better coordination. Ironically, it also creates more joint problems requiring joint solutions – and the rest of the world will be watching the proceedings, noting lack of cooperation.

Final thoughts

The real challenges for our technological future are complexity and risk.

We have in many ways plucked the low-hanging fruits of simple, high-performance technologies that vastly extend our reach in energy, material wealth, speed and so on, but run into subtler limits due to the complexity of the vast technological systems we need. The problem of writing software today is not memory or processing speed but handling a myriad of contingencies in distributed systems subject to deliberate attacks, emergence, localization, and technological obsolescence. Biotechnology can do wonders, yet has to contend with organic systems that have not been designed for upgradeability and spontaneously adapt to our interventions. Handling complex systems is going to be the great challenge for this century, requiring multidisciplinary research and innovations – and quite likely some new insights on the same level as the earth-shattering physical insights of the 20^th century.

More powerful technology is also more risky, since it can have greater consequences. The reach of the causal chains that can be triggered with a key press today are enormously longer than in 1957. Paradoxically, the technologies that threaten us also have the potential to help us reduce risk. Spaceflight makes ICBMs possible, but allows global monitoring and opens the possibility of becoming a multi-planetary species. Biotechnology allows for bioweapons, but also disease surveillance and rapid responses. Gene drives can control invasive species and disease vectors, or sabotage ecosystems. Surveillance can threaten privacy and political freedom, yet allow us to detect and respond to collective threats. Artificial intelligence can empower us, or produce autonomous technological systems that we have no control over. Handling risk requires both having an adequate understanding of what matters, designing the technologies, institutions or incentives that can reduce the risk – and convincing the world to use them.

The future of our species depends on what combination of technology, insight and coordination ability we have. Merely having one or two of them is not enough: without technology we are impotent, without insight we are likely to go in the wrong direction, and without coordination we will pull apart.

Fortunately, since 1957 I think we have not just improved our technological abilities, but we have shown a growth of insight and coordination ability. Today we are aware of global environmental and systemic problems to a new degree. We have integrated our world to an unprecedented degree, whether through international treaties, unions like the EU, or social media. We are by no means “there” yet, but we have been moving in the right direction. Hence I think we never had it so good.

[1]Freeman Dyson, Imagined Worlds. Harvard University Press (1997) P. 34-37, p. 183-185

[2] http://www.informationisbeautiful.net/visualizations/million-lines-of-code/

[3] https://en.wikipedia.org/wiki/Bell%27s_law_of_computer_classes

[4] https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/223114/diffs_life_expectancy_20_50_80.pdf

[5] http://www.beyondcurrenthorizons.org.uk/review-of-longevity-trends-to-2025-and-beyond/