After a recent lecture about the singularity I got asked about its energy requirements. It is a good question. As my inquirer pointed out, humanity uses more and more energy and it generally has an environmental cost. If it keeps on growing exponentially, something has to give. And if there is a real singularity, how do you handle infinite energy demands?

First I will look at current trends, then different models of the singularity.

I will not deal directly with environmental costs here. They are relative to some idea of a value of an environment, and there are many ways to approach that question.

Current trends

Current computers are energy hogs. Currently general purpose computing consumes about one Petawatt-hour per year, with the entire world production somewhere above 22 Pwh. While large data centres may be obvious, the vast number of low-power devices may be an even more significant factor; up to 10% of our electricity use may be due to ICT.

Together they perform on the order of $10^{20}$ operations per second, or somewhere in the zettaFLOPS range.

Koomey’s law states that the number of computations per joule of energy dissipated has been doubling approximately every 1.57 years. This might speed up as the pressure to make efficient computing for wearable devices and large data centres makes itself felt. Indeed, these days performance per watt is often more important than performance per dollar.

Meanwhile, general-purpose computing capacity has a growth rate of 58% per annum, doubling every 18 months. Since these trends cancel rather neatly, the overall energy need is not changing significantly.

The push for low-power computing may make computing greener, and it might also make other domains more efficient by moving tasks to the virtual world, making them efficient and allowing better resource allocation. On the other hand, as things become cheaper and more efficient usage tends to go up, sometimes outweighing the gain. Which trend wins out in the long run is hard to predict.

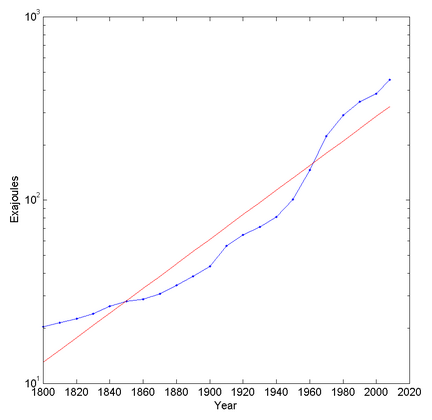
Semilog plot of global energy consumption over time. — Semilog plot of global energy (all types) consumption over time.

Looking at overall energy use trends it looks like overall energy use increases exponentially (but has stayed at roughly the same per capita level since the 1970s). In fact, plotting it on a semilog graph suggests that it is increasing faster than exponential (otherwise it would be a straight line). This is presumably due to a combination of population increase and increased energy use. The best fit exponential has a doubling time of 44.8 years.

Electricity use is also roughly exponential, with a doubling time of 19.3 years. So we might be shifting more and more to electricity, and computing might be taking over more and more of that.

Extrapolating wildly, we would need the total solar input on Earth in about 300 years and the total solar luminosity in 911 years. In about 1,613 years we would have used up the solar system’s mass energy. So, clearly, long before then these trends will break one way or another.

Physics places a firm boundary due to the Landauer principle: in order to erase on bit of information $k T \ln(2)$ joules of energy have to be dissipated. Given current efficiency trends we will reach this limit around 2048.

The principle can be circumvented using reversible computation, either classical or quantum. But as I often like to point out, it still bites in the form of the need for error correction (erasing accidentally flipped bits) and formatting new computational resources (besides the work in turning raw materials into bits). We should hence expect a radical change in computation within a few decades, even if the cost per computation and second continues to fall exponentially.

What kind of singularity?

But how many joules of energy does a technological singularity actually need? It depends on what kind of singularity. In my own list of singularity meanings we have the following kinds:

A. Accelerating change
B. Self improving technology
C. Intelligence explosion
D. Emergence of superintelligence
E. Prediction horizon
F. Phase transition
G. Complexity disaster
H. Inflexion point
I. Infinite progress

Case A, acceleration, at first seems to imply increasing energy demands, but if efficiency grows faster they could of course go down.

Eric Chaisson has argued that energy rate density, how fast and densely energy get used (watts per kilogram), might be an indicator of complexity and growing according to a universal tendency. By this account, we should expect the singularity to have an extreme energy rate density – but it does not have to be using enormous amounts of energy if it is very small and light.

He suggests energy rate density may increase as Moore’s law, at least in our current technological setting. If we assume this to be true, then we would have $\Phi(t) = \exp(kt) = P(t)/M(t)$ , where $P(t)$ is the power of the system and $M(t)$ is the mass of the system at time t. One can maintain exponential growth by reducing the mass as well as increasing the power.

However, waste heat will need to be dissipated. If we use the simplest model where a radius R system with density $\rho$ radiates it away into space, then the temperature will be $T=[\rho \Phi R/3 \sigma]^{1/4}$ , or, if we have a maximal acceptable temperature, $R < 3\sigma T^4 / \rho \Phi$ . So the system needs to become smaller as $\Phi$ increases. If we use active heat transport instead (as outlined in my previous post), covering the surface with heat pipes that can remove X watts/square meter, then $R < 3 X$ $/ \Phi \rho$ . Again, the radius will be inversely proportional to $\Phi$ . This is similar to our current computers, where the CPU is a tiny part surrounded by cooling and energy supply.

If we assume the waste heat is just due to erasing bits, the rate of computation will be $I = P/kT \ln(2) = \Phi M / kT\ln(2) = [4 \pi \rho /3 k \ln(2)] \Phi R^3 / T$ bits per second. Using the first cooling model gives us $I \propto T^{11}/ \Phi^2$ – a massive advantage for running extremely hot and dense computation. In the second cooling model $I \propto \Phi^{-2}$ : in both cases higher energy rate densities make it harder to compute when close to the thermodynamic limit. Hence there might be an upper limit to how much we may want to push $\Phi$ .

Also, a system with mass M will use up its own mass-energy in time $Mc^2/P = c^2/\Phi$ : the higher the rate, the faster it will run out (and it is independent of size!). If the system is expanding at speed v it will gain and use up mass at a rate $M'= 4\pi\rho v t^2 - M\Phi(t)/c^2$ ; if $\Phi$ grows faster than quadratic with time it will eventually run out of mass to use. Hence the exponential growth must eventually reduce simply because of the finite lightspeed.

The Chaisson scenario does not suggest a “sustainable” singularity. Rather, it suggests a local intense transformation involving small, dense nuclei using up local resources. However, such local “detonations” may then spread, depending on the long-term goals of involved entities.

Cases B, C, D (intelligence explosions, superintelligence) have an unclear energy profile. We do not know how complex code would become or what kind of computational search is needed to get to superintelligence. It could be that it is more a matter of smart insights, in which case the needs are modest, or a huge deep learning-like project involving massive amounts of data sloshing around, requiring a lot of energy.

Case E, a prediction horizon, is separate from energy use. As this essay shows, there are some things we can say about superintelligent computational systems based on known physics that likely remains valid no matter what.

Case F, phase transition, involves a change in organisation rather than computation, for example the formation of a global brain out of previously uncoordinated people. However, this might very well have energy implications. Physical phase transitions involve discontinuities of the derivatives of the free energy. If the phases have different entropies (first order transitions) there has to be some addition or release of energy. So it might actually be possible that a societal phase transition requires a fixed (and possibly large) amount of energy to reorganize everything into the new order.

There are also second order transitions. These are continuous do not have a latent heat, but show divergent susceptibilities (how much the system responds to an external forcing). These might be more like how we normally imagine an ordering process, with local fluctuations near the critical point leading to large and eventually dominant changes in how things are ordered. It is not clear to me that this kind of singularity would have any particular energy requirement.

Case G, complexity disaster, is related to superexponential growth, such as the city growth model of Bettancourt, West et al. or the work on bubbles and finite time singularities by Didier Sornette. Here the rapid growth rate leads to a crisis, or more accurately a series of crises increasingly rapidly succeeding each other until a final singularity. Beyond that the system must behave in some different manner. These models typically predict rapidly increasing resource use (indeed, this is the cause of the crisis sequence as one kind of growth runs into resource scaling problems and is replaced with another one), although as Sornette points out the post-singularity state might well be a stable non-rivalrous knowledge economy.

Case H, an inflexion point, is very vanilla. It would represent the point where our civilization is halfway from where we started to where we are going. It might correspond to “peak energy” where we shift from increasing usage to decreasing usage (for whatever reason), but it does not have to. It could just be that we figure out most physics and AI in the next decades, become a spacefaring posthuman civilization, and expand for the next few billion years, using ever more energy but not having the same intense rate of knowledge growth as during the brief early era when we went from hunter gatherers to posthumans.

Case I, infinite growth, is not normally possible in the physical universe. Information can as far as we know not be stored beyond densities set by the Bekenstein bound ( $I \leq k_I MR$ where $k_I\approx 2.577\cdot 10^{43}$ bits per kg per meter), and we only have access to a volume $4 \pi c^3 t^3/3$ with mass density $\rho$ , so the total information growth must be bounded by $I \leq 4 \pi k_I c^4 \rho t^4/3$ . It grows quickly, but still just polynomially.

The exception to the finitude of growth is if we approach the boundaries of spacetime. Frank J. Tipler’s omega point theory shows how information processing could go infinite in a finite (proper) time in the right kind of collapsing universe with the right kind of physics. It doesn’t look like we live in one, but the possibility is tantalizing: could we arrange the right kind of extreme spacetime collapse to get the right kind of boundary for a mini-omega? It would be way beyond black hole computing and never be able to send back information, but still allow infinite experience. Most likely we are stuck in finitude, but it won’t hurt poking at the limits.

Conclusions

Indefinite exponential growth is never possible for physical properties that have some resource limitation, whether energy, space or heat dissipation. Sooner or later they will have to shift to a slower rate of growth – polynomial for expanding organisational processes (forced to this by the dimensionality of space, finite lightspeed and heat dissipation), and declining growth rate for processes dependent on a non-renewable resource.

That does not tell us much about the energy demands of a technological singularity. We can conclude that it cannot be infinite. It might be high enough that we bump into the resource, thermal and computational limits, which may be what actually defines the singularity energy and time scale. Technological singularities may also be small, intense and localized detonations that merely use up local resources, possibly spreading and repeating. But it could also turn out that advanced thinking is very low-energy (reversible or quantum) or requires merely manipulation of high level symbols, leading to a quiet singularity.

My own guess is that life and intelligence will always expand to fill whatever niche is available, and use the available resources as intensively as possible. That leads to instabilities and depletion, but also expansion. I think we are – if we are lucky and wise – set for a global conversion of the non-living universe into life, intelligence and complexity, a vast phase transition of matter and energy where we are part of the nucleating agent. It might not be sustainable over cosmological timescales, but neither is our universe itself. I’d rather see the stars and planets filled with new and experiencing things than continue a slow dance into the twilight of entropy.

…contemplate the marvel that is existence and rejoice that you are able to do so. I feel I have the right to tell you this because, as I am inscribing these words, I am doing the same.
– Ted Chiang, Exhalation

Andart II

Part of Anders' Exoself

Energy requirements of the singularity

Current trends

What kind of singularity?

Conclusions

Leave a Reply Cancel reply