Zach Weinersmith asked:
For a joke (I promise): what’s the cheapest source of neutrons? Uranium ore?
— Zach Weinersmith (@ZachWeiner) May 11, 2017
That is a great question. I once came up with the answer “50 tons of neutrons are needed” to a serious problem (you don’t want to know). How cheaply could you get that?
Figuring out roughly how many neutrons there are per kilogram of pure elements is pretty easy. Get their standard atomic weights, , and subtract the atomic number
since that is the number of protons:
. Now we know how many neutrons there are per atom on average (standard atomic weights include the different isotope weights, weighted by their abundance).
[ Since nucleons (protons and neutrons) are about 1830 times heavier than electrons, we can ignore the electrons for an error on order of 0.05%. There is also a binding energy error, since some of the total atomic mass is because of binding energy between nucleons, which is 0.94% or less. These errors are nothing compared to price uncertainties.]
We know that one nucleon weighs about kg, so the number of nucleons per kilogram is
and the number of neutrons per kilo is
. This ranges from
for helium down to
for Oganesson. Hydrogen just has
neutrons per kilogram, despite having
nucleons per kilogram – there isn’t that much deuterium and tritium around to contribute neutrons.
Now, the price of elements is badly defined. I can get a kilogram of coal much cheaper than a kilogram of diamond, and ultra-pure elements are very expensive even if the everyday element is cheap. Plus, prices vary. And it is hard to buy plutonium on the open market. Ignoring all that and taking the numbers from Wikipedia (and ignoring the that some values look odd, and some are for compounds, and that the prices are unadjusted for inflation, and that they are lacking for many elements…) we can actually calculate the number of neutrons per dollar:
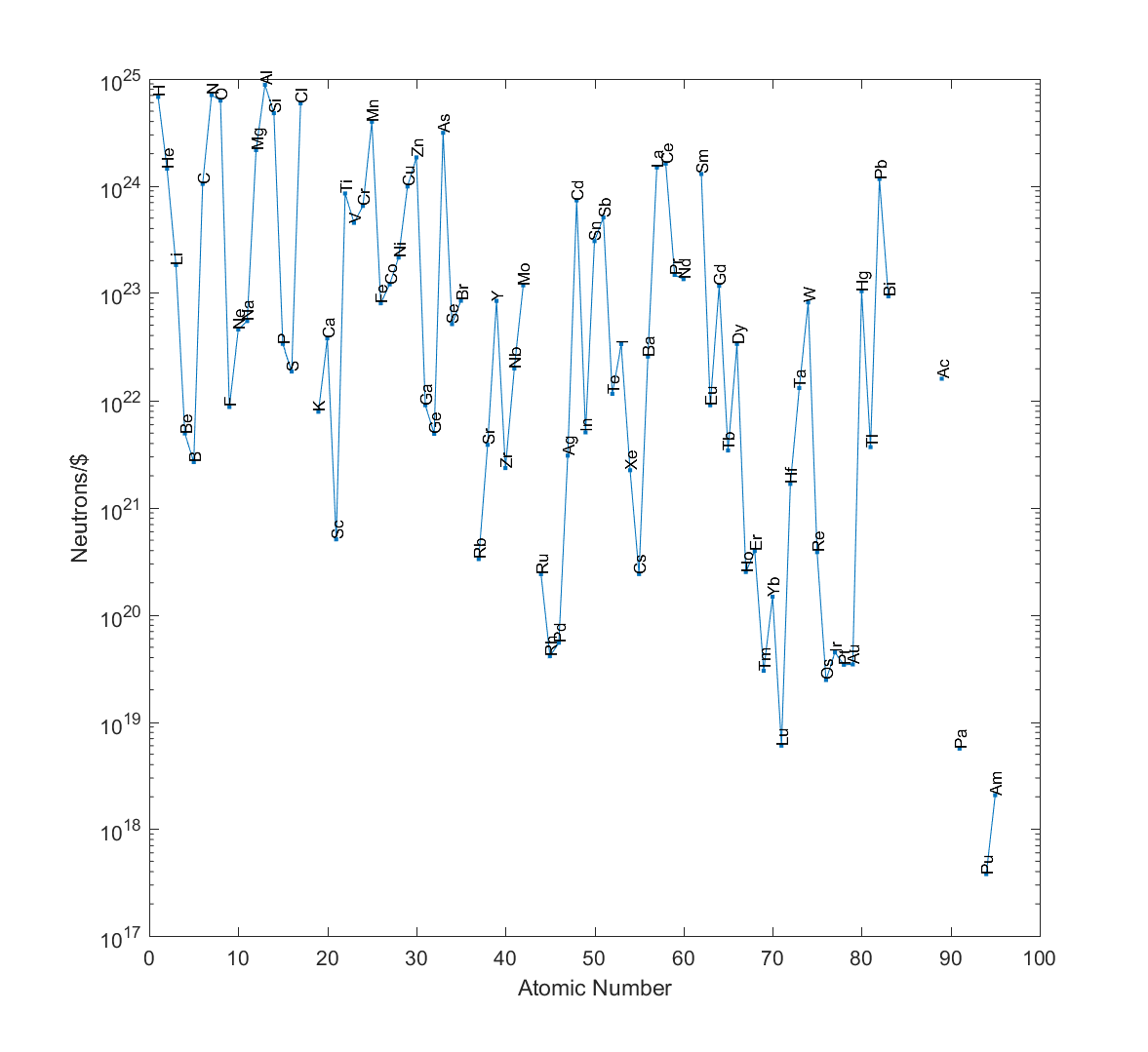
And the winner is… aluminium! You can get neutrons per dollar from aluminium.
In second place, nitrogen () and in third, hydrogen (
)! Hydrogen may be very neutron-poor, but since it is rather cheap and you get lots of nucleons per kilo, this balances the lack.
Given that these prices are dodgy, I would expect an uncertainty on the order of a magnitude (at least). So the true winner, given the cheapest actual source of the element, might be hard to find without excruciating price comparisons. But we can be fairly certain it is going to be something with an atomic number less than 25. Uranium is unlikely to be a cheap neutron source in this sense (and just look at poor plutonium!)
So, given that aluminium is 51.8% neutrons by weight I need 96.5 tons. The current aluminium price is $1,650.00 per ton, so I would have to pay $159,225 for the neutrons in my doomsday weapon – I mean, totally innocuous thought experiment!
Okay, but why do we have to use a pure element? What about tap water?
I calculate that would cost about $120.
Facepalm. I should have thought about it. A colleague also pointed it out.
A liter of water has 3.344e25 molecules, each with 8.0150 neutrons. http://hypertextbook.com/facts/2004/JosephSabatelle.shtml gives a price range from 0.000108 (tap water) to 0.46 $/l (bottled). So that gives us between 2.4817e30 and 5.8266e26 neutrons/$. Even fancy bottled water is cost effective!