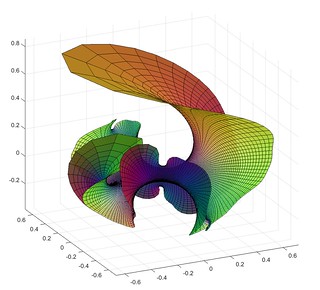
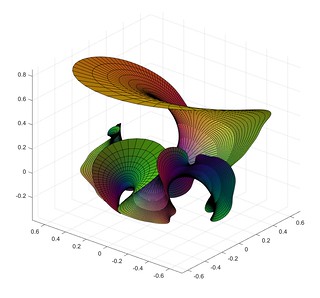
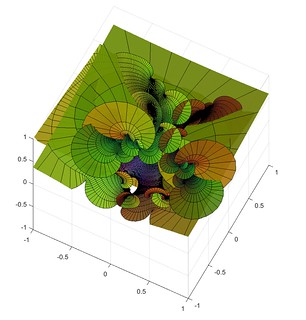
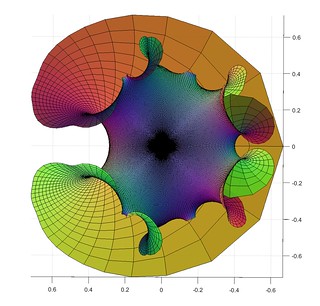
A short while ago I mentioned lacunary functions, complex functions that are analytic inside a disc but cannot be continued outside it. Then I remembered the wonderful Weierstrass-Enneper representation formula, which assigns a minimal surface to (nearly) any pair of complex functions. What happens when you make a minimal surface from a lacunary function?
I was not first with this idea. In fact, F.F. de Brito used this back in 1992 to demonstrate that there exist complete embedded minimal surfaces in 3-space that are contained between two planes.
Here is the surface defined by the function , the Taylor series that only includes all prime powers, combined with
.
Close to zero, the surface is flat. Away from zero it begins to wobble as increasingly high powers in the series begin to dominate. It behaves very much like a higher-degree Enneper surface, but with a wobble that is composed of smaller wobbles. It is cool to consider that this apparently irregular pattern corresponds to the apparently irregular pattern of all primes.