Here is a minimal surface based on the Weierstrass-Enneper representation 
![\Re([-\tanh(z)(\mathrm{sech}^2(z)-4)/6,i(6z+\tanh(z)(\mathrm{sech}^2(z)-4))/6,z-\tanh(z)])](https://s0.wp.com/latex.php?latex=%5CRe%28%5B-%5Ctanh%28z%29%28%5Cmathrm%7Bsech%7D%5E2%28z%29-4%29%2F6%2Ci%286z%2B%5Ctanh%28z%29%28%5Cmathrm%7Bsech%7D%5E2%28z%29-4%29%29%2F6%2Cz-%5Ctanh%28z%29%5D%29&bg=ffffff&fg=000000&s=0 "\Re([-\tanh(z)(\mathrm{sech}^2(z)-4)/6,i(6z+\tanh(z)(\mathrm{sech}^2(z)-4))/6,z-\tanh(z)])")
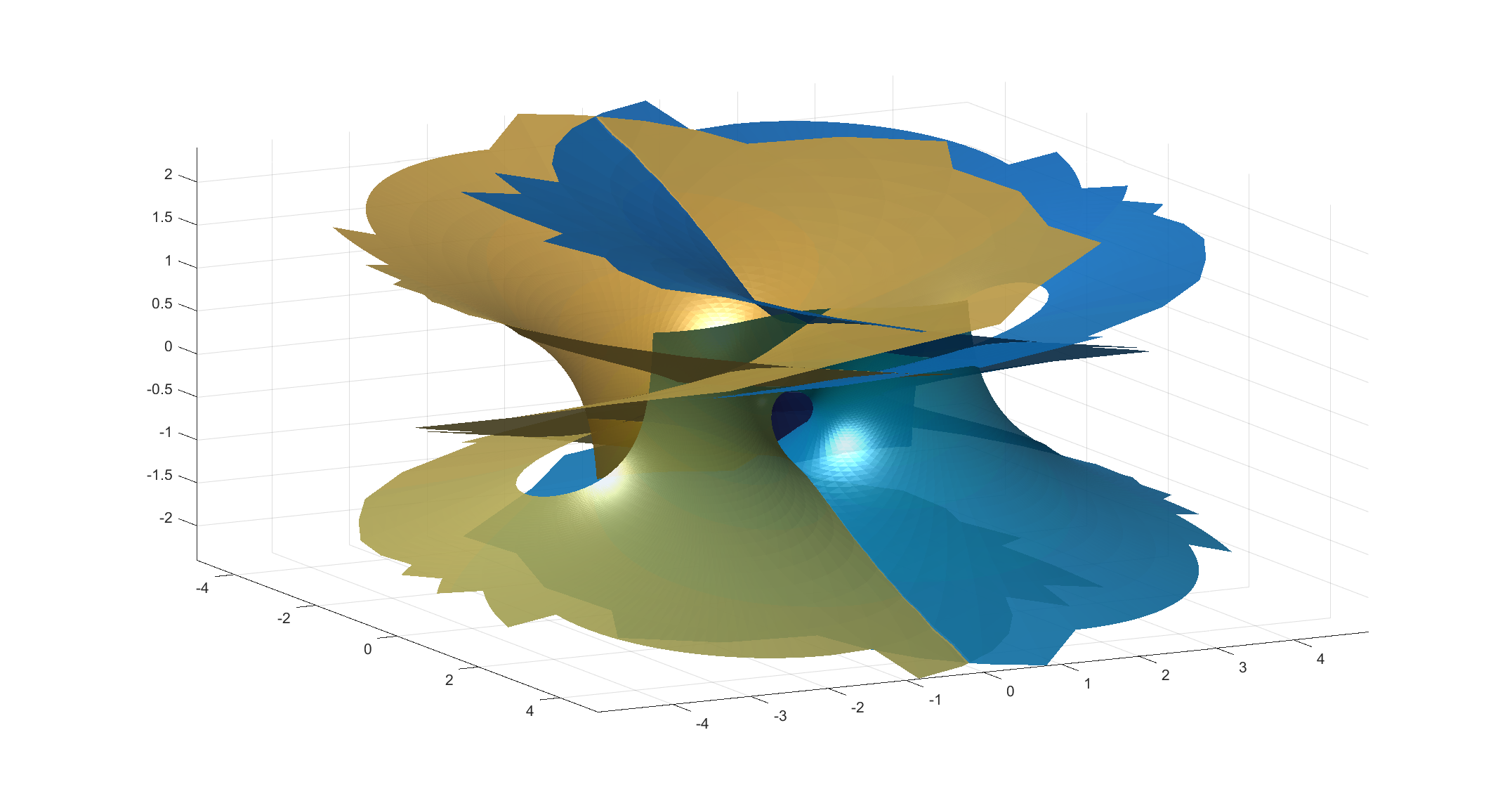
It is based on my old tanh surface, but has a wilder style. It gets helped by the fact that my triangulation in the picture is pretty jagged. On one hand it has two flat ends, but also a infinite number of catenoid openings (only two shown here).
I call it Håkan’s surface, since I came up with it on my dear husband’s birthday. Happy birthday, Håkan!