The Annihilation Score as Satirical Sociology

Today I read The Annihilation Score by Charles Stross during a flight. It is the sixth Laundry novel, and in many ways the weakest. But it might be the intellectually and satirically best.

The Laundry novels are a mix of horror, spy story, geekiness, and satire. This is both a reader-winning combination (transitions from one side of the mixture to another can provide intense contrast, and Stross can give readers a bit of everything) and a balancing problem: each story needs to maintain the right mixture, and the readers often have their own favourite ratios. The Annihilation Score goes further in the direction of satire, reducing the horror and geekiness fairly significantly. This no doubt makes many Laundry fans unhappy. Me too, to some extent: there is nothing more delightful than noticing wordplay based on obscure hermetica and computer science, or the distinctly unsettling implications of thinking through some of the metaphysical assumptions of the setting. However, I think Stross hit on something different in this novel: an important argument disguised as satire.

On the surface the novel suffers from bad pacing: the bulk of it is about management. Not intense action, but rather the issue of how to set up an office, from personnel management to furniture to keeping the funding body happy despite contradictory goals. There is plenty of agency-spotting, with numerous acronymical organisations criss-crossing the story with their interleaved agendas. And finally, in the last fifth, a climactic battle. Typically Laundry novels spend a lot of times establishing a mood and tension for a relatively brief finale where they get unleashed. The Annihilation Score takes this even further, but at least I did not feel much of a build-up. In fact, despite the pressure on the main character she comes across as almost a Westminster Mary Sue: she persists and succeeds at nearly everything, from turning what ought to be a social nightmare into a cozy core team, to handling unseen budgetary constraints.

However, on a deeper level this is not a horror story about inhuman entities from other dimensions threatening to invade our world and their misguided human servants. This is a horror story about the inhuman entity inhabiting Whitehall: government.

Taking jabs at the absurdity, stupidity and inhumanity of bureaucracy has been a staple in the Laundry books. What makes the Annihilation Score stand out is that it actually has a fairly well thought out argument and exposition of why. The basics are familiar from the earlier novels: the iron law of bureaucracy (framed here as the emergent instrumental goal of organisations to preserve themselves), Parkinson’s law, the Snafu principle, empire building, not invented here, in-group out-group dynamics, Something Must Be Done, and so on. The novel does a sociological dive into the internal culture of the subset of bureaucracy dealing with policing. Here there exists a strong ethos about what purpose it actually has, which both serves to recruit and advance people with a compatible mindset and actually maintain some mission focus. Presumably because it would be very noticeable if the police force began too drift too far from its necessary function; compare this with how some branches of academia are kept honest by constant interaction with an unyielding real world, and others diffuse into obscure absurdity since there are only social forces constraining them. But even when a purpose has an apparently clear meaning it can get subtly (or not so subtly) twisted. This is especially true at the top, where the constraints of external practical reality are weakest.

Stross examines the case where bureaucracy recognizes it has an out-of-context problem. Something important yet unknown is intruding, and clearly something must be done to handle it. The problem is of course that following the politician’s syllogism means that whatever fast and decisive action is taken is not going to be based on good knowledge. Worse, if the organisation is centred on dealing with something Very Important like national security it will hence be (1) extremely motivated to do it, (2) discount signals from unimportant (as described by its own value system) organisations or sources. A not so subtle analogy to the Annihilation Score is government handling of many emerging technologies such as encryption. Internal expertise is lacking not just on the technology itself and its full implications, but there is also a lack of expertise in judging the consequences of different actions and expertise in recognizing this kind of expertise.

This is where I think the novel actually succeeds: it plays out a satirical scenario, but the parts are all-too-familiar. Well-meaning people work hard to ensure something agreed to be good, and the result is Moloch. The Sleeper in the Pyramid is not half as scary as the Dweller in Whitehall. Because the later is real.

What is the natural timescale for making a Dyson shell?

KIC 8462852 (“Tabby’s Star”) continues to confuse. I blogged earlier about why I doubt it is a Dyson sphere. SETI observations in radio and optical has not produced any finds. Now there is evidence that it has dimmed over a century timespan, something hard to square with the comet explanation. Phil Plait over at Bad Astronomy has a nice overview of the headscratching.

However, he said something that I strongly disagree with:

Now, again, let me be clear. I am NOT saying aliens here. But, I’d be remiss if I didn’t note that this general fading is sort of what you’d expect if aliens were building a Dyson swarm. As they construct more of the panels orbiting the star, they block more of its light bit by bit, so a distant observer sees the star fade over time.

However, this doesn’t work well either. … Also, blocking that much of the star over a century would mean they’d have to be cranking out solar panels.

Basically, he is saying that a century timescale construction of a Dyson shell is unlikely. Now, since I have argued that we could make a Dyson shell in about 40 years, I disagree. I got into a Twitter debate with Karim Jebari (@KarimJebari) about this, where he also doubted what the natural timescale for Dyson construction is. So here is a slightly longer than Twitter message exposition of my model.

Lower bound

There is a strict lower bound set by how long it takes for the star to produce enough energy to overcome the binding energy of the source bodies (assuming one already have more than enough collector area). This is on the order of days for terrestrial planets, as per Robert Bradbury’s original calculations.

Basic model

Starting with a small system that builds more copies of itself, solar collectors and mining equipment, one can get exponential growth.

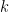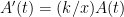A simple way of reasoning: if you have an area $A(t)$ of solar collectors, you will have energy $kA(t)$ to play with, where $k$ is the energy collected per square meter. This will be used to lift and transform matter into more collectors. If we assume this takes $x$ Joules per square meter on average, we get $A'(t) = (k/x)A(t)$ , which makes $A(t)$ is an exponential function with time constant $k/x$ . 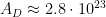If a finished Dyson shell has area $A_D\approx 2.8\cdot 10^{23}$ meters and we start with an initial plant of size 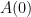$A(0)$ (say on the order of a few hundred square meters), then the total time to completion is $t = (x/k)\ln(A_D/A(0))$ seconds. The logarithmic factor is about 50.

If we assume $k \approx 3\cdot 10^2$ W and $x \approx 40.15$ MJ/kg (see numerics below), then t=78 days.

This is very much in line with Robert’s original calculations. He pointed out that given the sun’s power output Earth could be theoretically disassembled in 22 days. In the above calculations the time constant (the time it takes to get 2.7 times as much area) is 37 hours. So for most of the 78 days there is just a small system expanding, not making a significant dent in the planet nor being very visible over interstellar distances; only in the later part of the period will it start to have radical impact.

The timescale is robust to the above assumptions: sun-like main sequence stars have luminosities within an order of magnitude of the sun (so 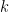$k$ can only change a factor of 10), using asteroid material (no gravitational binding cost) brings down $x$ by a factor of 10; if the material needs to be vaporized $x$ increases by less than a factor of 10; if a sizeable fraction of the matter is needed for mining/transport/building systems $x$ goes down proportionally; much thinner shells (see below) may give three orders of magnitude smaller $x$ (and hence bump into the hard bound above). So the conclusion is that for this model the natural timescale of terrestrial planetary disassembly into Dyson shells is on the order of months.

Digging into the practicalities of course shows that there are some other issues. Material needs to be transported into place (natural timescale about a year for a moving something 1 AU), the heating effects are going to be major on the planet being disassembled (lots of energy flow there, but of course just boiling it into space and capturing the condensing dust is a pretty good lifting method), the time it takes to convert 1 kg of undifferentiated matter into something useful places a limit of the mass flow per converting device, and so on. This is why our conservative estimate was 40 years for a Mercury-based shell: we assumed a pretty slow transport system.

Numerical values

Estimate for $x$ : assuming that each square meter shell has mass 1 kg, that the energy cost comes from the mean gravitational binding energy of Earth per kg of mass (37.5 MJ/kg), plus processing energy (on the order of 2.65 MJ/kg for heating and melting silicon). Note that using Earth slows things significantly.

I had a conversation with Eric Drexler today, where he pointed out that assuming 1 kg/square meter for the shell is arbitrary. There is a particular area density that is special: given that solar gravity and light pressure both decline with the square of the distance, there exists a particular density 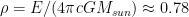$\rho=E/(4 \pi c G M_{sun})\approx 0.78$ gram per square meter, which will just hang there neutrally. Heavier shells will need to orbit to remain where they are, lighter shells need cables or extra weight to not blow away. This might hence be a natural density for shells, making $x$ a factor 1282 smaller.

Linear growth does not work

I think the key implicit assumption in Plait’s thought above is that he imagines some kind of alien factory churning out shell. If it produces it at a constant rate 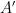$A'$ , then the time until it a has produced a finished Dyson shell with area 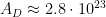$A_D\approx 2.8\cdot 10^{23}$ square meters. That will take 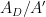$A_D/A'$ seconds.

Current solar cell factories produce on the order of a few hundred MW of solar cells per year; assuming each makes about 2 million square meters per year, we need 140 million billion years. Making a million factories merely brings things down to 140 billion years. To get a century scale dimming time, 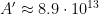$A' \approx 8.9\cdot 10^{13}$ square meters per second, about the area of the Atlantic ocean.

This feels absurd. Which is no good reason for discounting the possibility.

Automation makes the absurd normal

As we argued in our paper, the key assumptions are (1) things we can do can be automated, so that if there are more machines doing it (or doing it faster) there will be more done. (2) we have historically been good at doing things already occurring in nature. (3) self-replication and autonomous action occurs in nature. 2+3 suggests exponentially growing technologies are possible where a myriad entities work in parallel, and 1 suggests that this allows functions such as manufacturing to be scaled up as far as the growth goes. As Kardashev pointed out, there is no reason to think there is any particular size scale for the activities of a civilization except as set by resources and communication.

Incidentally, automation is also why cost overruns or lack of will may not matter so much for this kind of megascale projects. The reason Intel and AMD can reliably make billions of processors containing billions of transistors each is that everything is automated. Making the blueprint and fab pipeline is highly complex and requires an impressive degree of skill (this is where most overruns and delays happen), but once it is done production can just go on indefinitely. The same thing is true of Dyson-making replicators. The first one may be a tough problem that takes time to achieve, but once it is up and running it is autonomous and merely requires some degree of watching (make sure it only picks apart the planets you don’t want!) There is no requirement of continued interest in its operations to keep them going.

Likely growth rates

But is exponential growth limited mostly by energy the natural growth rate? As Karim and others have suggested, maybe the aliens are lazy or taking their time? Or, conversely, that multi century projects are unexpectedly long-term and hence rare.

Obviously projects could occur with any possible speed: if something can construct something in time X, it can in generally be done half as fast. And if you can construct something of size X, you can do half of it. But not every speed or boundary is natural. We do not answer the question of why a forest or the Great Barrier reef have the size they do by cost overruns stopping them, or that they will eventually grow to arbitrary size, but the growth rate is so small that it is imperceptible. The spread of a wildfire is largely set by physical factors, and a static wildfire will soon approach its maximum allowed speed since part of the fire that do not spread will be overtaken by parts that do. The same is true for species colonizing new ecological niches or businesses finding new markets. They can run slow, it is just that typically they seem to move as fast as they can.

Human economic growth has been on the order of 2% per year for very long historical periods. That implies a time constant 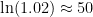$\ln(1.02)\approx 50$ years. This is a “stylized fact” that remained roughly true despite very different technologies, cultures, attempts at boosting it, etc. It seems to be “natural” for human economies. So were a Dyson shell built as a part of a human economy, we might expect it to be completed in 250 years.

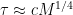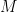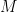What about biological reproduction rates? Merkle and Freitas lists the replication time for various organisms and machines. They cover almost 25 orders of magnitude, but seem to roughly scale as $\tau \approx c M^{1/4}$ , where $M$ is the mass and $c\approx 10^7$ . So if a total mass $M_T$ needs to be converted into replicators of mass $M$ , it will take time $t=\tau\ln(M_T)/\ln(2)$ . Plugging in the first formula gives 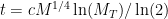$t=c M^{1/4} \ln(M_T)/\ln(2)$ . The smallest independent replicators have 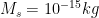$M_s=10^{-15} kg$ (this gives 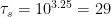$\tau_s=10^{3.25}=29$ minutes) while a big factory-like replicator (or a tree!) would have 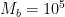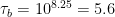$M_b=10^5$ ( $\tau_b=10^{8.25}=5.6$ years). In turn, if we set $M_T=A_D\rho=2.18\cdot 10^{20}$ (a “light” Dyson shell) the time till construction ranges from 32 hours for the tiny to 378 years for the heavy replicator. 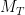Setting $M_T$ to an Earth mass gives a range from 36 hours to 408 years.

The lower end is infeasible, since this model assumes enough input material and energy – the explosive growth of bacteria-like replicators is not possible if there is not enough energy to lift matter out of gravity wells. But it is telling that the upper end of the range is merely multi-century. This makes a century dimming actually reasonable if we think we are seeing the last stages (remember, most of the construction time the star will be looking totally normal); however, as I argued in my previous post, the likelihood of seeing this period in a random star being englobed is rather low. So if you want to claim it takes millennia or more to build a Dyson shell, you need to assume replicators that are very large and heavy.

[Also note that some of the technological systems discussed in Merkle & Freitas are significantly faster than the main branch. Also, this discussion has talked about general replicators able to make all their parts: if subsystems specialize they can become significantly faster than more general constructors. Hence we have reason to think that the upper end is conservative.]

Conclusion

There is a lower limit on how fast a Dyson shell can be built, which is likely on the order of hours for manufacturing and a year of dispersion. Replicator sizes smaller than a hundred tons imply a construction time at most a few centuries. This range includes the effect of existing biological and economic growth rates. We hence have a good reason to think most Dyson construction is fast compared to astronomical time, and that catching a star being englobed is pretty unlikely.

I think that models involving slowly growing Dyson spheres require more motivation than models where they are closer to the limits of growth.

A prime minimal surface

A short while ago I mentioned lacunary functions, complex functions that are analytic inside a disc but cannot be continued outside it. Then I remembered the wonderful Weierstrass-Enneper representation formula, which assigns a minimal surface to (nearly) any pair of complex functions. What happens when you make a minimal surface from a lacunary function?

I was not first with this idea. In fact, F.F. de Brito used this back in 1992 to demonstrate that there exist complete embedded minimal surfaces in 3-space that are contained between two planes.

Here is the surface defined by the function $g(z)=\sum_{p \mathrm{is prime}} z^p$ , the Taylor series that only includes all prime powers, combined with $f(z)=1$ .

Close to zero, the surface is flat. Away from zero it begins to wobble as increasingly high powers in the series begin to dominate. It behaves very much like a higher-degree Enneper surface, but with a wobble that is composed of smaller wobbles. It is cool to consider that this apparently irregular pattern corresponds to the apparently irregular pattern of all primes.

Predictions for 2016

The ever readable Slate Star Codex has a post about checking how accurate the predictions for 2015 were; overall Scott Alexander seems pretty well calibrated. Being a born follower I decided to make a bunch of predictions to check my calibration in a year’s time.

Here is my list of predictions, with my confidence (some predictions obviously stolen):

No nuclear war: 99%
No terrorist attack in the USA will kill > 100 people: 95%
I will be involved in at least one published/accepted-to-publish research paper by the end of 2015: 95%
Vesuvius will not have a major eruption: 95%
I will remain at my same job through the end of 2015: 90%
MAX IV in Lund delivers X-rays: 90%
Andart II will remain active: 90%
Israel will not get in a large-scale war (ie >100 Israeli deaths) with any Arab state: 90%
US will not get involved in any new major war with death toll of > 100 US soldiers: 90%
New Zeeland has not decided to change current flag at end of year: 85%
No multi-country Ebola outbreak: 80%
Assad will remain President of Syria: 80%
ISIS will control less territory than it does right now: 80%
North Korea’s government will survive the year without large civil war/revolt: 80%
The US NSABB will allow gain of function funding: 80%
US presidential election: democratic win: 75%
A general election will be held in Spain: 75%
Syria’s civil war will not end this year: 75%
There will be no NEO with Torino Scale >0 on 31 Dec 2016: 75%
The Atlantic basin ACE will be below 96.2: 70%
Sweden does not get a seat on the UN Security Council: 70%
Bitcoin will end the year higher than $200: 70%
Another major eurozone crisis: 70%
Brent crude oil will end the year lower than $60 a barrel: 70%
I will actually apply for a UK citizenship: 65%
UK referendum votes to stay in EU: 65%
China will have a GDP growth above 5%: 65%
Evidence for supersymmetry: 60%
UK larger GDP than France: 60%
France GDP growth rate less than 2%: 60%
I will have made significant progress (4+ chapters) on my book: 55%
Iran nuclear deal holding: 50%
Apple buys Tesla: 50%
The Nikkei index ends up above 20,000: 50%

The point is to have enough that we can see how my calibration works.

Looking for topics leads to amusing finds like the predictions of Nostradamus for 2015. Given that language barriers remain, the dead remain dead, lifespans are less than 200, there has not been a Big One in western US nor has Vesuvius erupted, and taxes still remain, I think we can conclude he was wrong or the ability to interpret him accurately is near zero. Which of course makes his quatrains equally useless.

Some math for Epiphany

Analytic functions helping you out

Recently I chatted with a mathematician friend about generating functions in combinatorics. Normally they are treated as a neat symbolic trick: you have a sequence $a_n$ (typically how many there are of some kind of object of size $n$ ), you formally define a function $f(z)=\sum_{n=0}^\infty a_n z^n$ , you derive some constraints on the function, and from this you get a formula for the $a_n$ or other useful data. Convergence does not matter, since this is purely symbolic. We used this in our paper counting tie knots. It is a delightful way of solving recurrence relations or bundle up moments of probability distributions.

I innocently wondered if the function (especially its zeroes and poles) held any interesting information. My friend told me that there was analytic combinatorics: you can actually take $f(z)$ seriously as a (complex) function and use the powerful machinery of complex analysis to calculate asymptotic behavior for the $a_n$ from the location and type of the “dominant” singularities. He pointed me at the excellent course notes from a course at Princeton linked to the textbook by Philippe Flajolet and Robert Sedgewick. They show a procedure for taking combinatorial objects, converting them symbolically into generating functions, and then get their asymptotic behavior from the properties of the functions. This is extraordinarily neat, both in terms of efficiency and in linking different branches of math.

Plot of z/(1-z-z^2), the generating function of the Fibonacci numbers. It has poles at (1+sqrt(5))/2 (the dominant pole giving the overall asymptotic growth of Fibonacci numbers) and (1-sqrt(5))/2, which does not contribute much to the asymptotic behavior.

In our case, one can show nearly by inspection that the number of Fink-Mao tie knots grow with the number of moves as $\sim 2^n$ , while single tuck tie knots grow as $\sim \sqrt{6}^n$ .

Analytic functions behaving badly

The second piece of math I found this weekend was about random Taylor series and lacunary functions.

If $f(z)=\sum_{n=0}^\infty X_n z^n$ where $X_n$ are independent random numbers, what kind of functions do we get? Trying it with complex Gaussian $X_n$ produces a disk of convergence with some nondescript function on the inside.

Plot of function with a Gaussian Taylor series. Color corresponds to stereographic mapping of the complex plane to a sphere, with infinity being white and zeros black. The domain of convergence is the unit circle.

Replacing the complex Gaussian with a real one, or uniform random numbers, or even power-law numbers gives the same behavior. They all seem to have radius 1. This is not just a vanilla disk of convergence (where an analytic function reaches a pole or singularity somewhere on the boundary but is otherwise fine and continuable), but a natural boundary – that is, a boundary so dense with poles or singularities that continuation beyond it is not possible at all.

The locus classicus about random Taylor series is apparently Kahane, J.-P. (1985), Some Random Series of Functions. 2nd ed., Cambridge University Press, Cambridge.

A naive handwave argument is that for $|z|<1$ we have an exponentially decaying sequence of $z^n$ , so if the $X_n$ have some finite average size $E(X)$ and not too divergent variance we should expect convergence, while outside the unit circle any nonzero $E(X)$ will allow it to diverge. We can even invoke the Markov inequality $P(X>t) \leq E(X)/t$ to argue that a series $\sum X_n f(n)$ would converge if $\sum f(n)/n$ converges. However, this is not correct enough for proper mathematics. One entirely possible Gaussian outcome is $X_n=1,10,100,1000,\ldots$ or worse. We need to speak of probabilistic convergence.

Andrés E. Caicedo has a good post about how to approach it properly. The “trick” is the awesome Kolmogorov zero-one law that implies that since the radius of convergence depends on the entire series X_n rather than any finite subset (and they are all independent) it will be a constant.

This kind of natural boundary disk of convergence may look odd to beginning students of complex analysis: after all, none of the functions we normally encounter behave like this. Except that this is of course selection bias. If you look at the example series for lacunary functions they all look like fairly reasonable sparse Taylor series like $z+z^4+z^8+z^16+^32+\lddots$. In calculus we are used to worrying that the coefficients in front of the z-terms of a series don’t diminish fast enough: having fewer nonzero terms seems entirely innocuous. But as Hadamard showed, it is enough that the size of the gaps grow geometrically for the function to get a natural boundary (in fact, even denser series do this – for example having just prime powers). The same is true for Fourier series. Weierstrass’ famous continuous but nowhere differentiable function is lacunary (in his 1880 paper on analytic continuation he gives the example $\sum a_n z^{b^n}$ of an uncontinuable function). In fact, as Emile Borel found and Steinhardt eventually proved in a stricter sense, in general (“almost surely”) a Taylor series isn’t continuable because of boundaries.

The function sum_p z^p, where p runs over the primes. — The function [latex]sum_p z^p[/latex], where [latex]p[/latex] runs over the primes.

One could of course try to combine the analytic combinatorics with the lacunary stuff. In a sense a lacunary generating function is a worst case scenario for the singularity-measuring methods used in analytical combinatorics since you get an infinite number of them at a finite and equal distance, and now have to average them together somehow. Intuitively this case seems to correspond to counting something that becomes rarer at a geometric rate or faster. But the Borel-Steinhardt results suggest that even objects that do not become rare could have nasty natural boundaries – if the number $a_n$ were due to something close enough to random we should expect estimating asymptotics to be hard. The funniest example I can think of is the number of roots of Chaitin-style Diophantine equations where for each $n$ it is an independent arithmetic fact whether there are any: this is hardcore random, and presumably the exact asymptotic growth rate will be uncomputable both practically and theoretically.

Andart II

Part of Anders' Exoself

Month: January 2016