Browsing Mindfuck Math I came across a humorous Venn diagram originally from Spikedmath.com. It got me to look up the Borwein integral. Wow. A kind of mathematical anti-beauty.
“As we all know”, for
and defined to be 1 for
. It is not that uncommon as a function. Now look at the following series of integrals:
,
,
.
The pattern continues:
.
And then…
It is around 0.499999999992646 – nearly a half, but not quite.
What is going on here? Borwein & Borwein give proofs, but they are not entirely transparent. Basically the reason is that 1/3+1/5+…1/13 < 1, while 1/3+1/5+…1/13 + 1/15 > 1, but why this changes things is clear as mud. Thankfully Hanspeter Schmid has a very intuitive explanation that makes what is going on possible to visualize. At least if you like convolutions.
In any case, there is something simultaneously ugly and exciting when neat patterns in math just ends for no apparent reason.
Another good example is the story of the Doomsday conjecture. Gwern tells the story well, based on Klarreich: a certain kind of object is found in dimension 2, 6, 14, 30 and 62… aha! They are conjectured to occur in all dimensions. A branch of math was built on this conjecture… and then the pattern failed in dimension 254. Oops.
It is a bit like the opposite case of the number of regular convex polytopes in different dimensions: 1, infinity, 5, 6, 3, 3, 3, 3… Here the series start out crazy, and then becomes very regular.
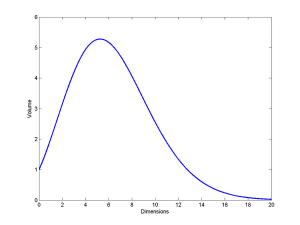
Another dimensional “imperfection” is the behaviour of the volume of the n-sphere:
The volume of a unit sphere increases with dimension until , and then decreases. Leaving the non-intuitiveness of why volumes would shrink aside, the real oddness is that the maximum is for a non-integer dimension. We might argue that the formula is needlessly general and only the integer values count, but many derivations naturally bring in the Gamma function and hence the possibility of non-integer values.
Another association is to this integral problem: given a set of integers , is the integral
? As shown in Moore and Mertens, this is NP-complete. Here the strangeness is that integrals normally are pretty well behaved. It seems absurd that a particular not very scary trigonometric integral should require exponential work to analyze. But in fact, multivariate integrals are NP-hard to approximate, and calculating the volume of a n-dimensional polytope is actually #P-complete.
We tend to assume that mathematics is smoother and more regular than reality. Everything is regular and exceptionless because it is generated by universal rules… except when it isn’t. The rules often act as constraints, and when they do not mesh exactly odd things happen. Similarly we may assume that we know what problems are hard or not, but this is an intuition built in our own world rather than the world of mathematics. Finally, some mathematical truths maybe just are. As Gregory Chaitin has argued, some things in math are irreducible; there is no real reason (at least in the sense of a comprehensive explanation) for why they are true.
Mathematical anti-beauty can be very deep. Maybe it is like the insects, rot and other memento mori in classical still life paintings: a deviation from pleasantness and harmony that adds poignancy and a bit of drama. Or perhaps more accurately, it is wabi-sabi.
I’m very much enjoying the revised Andart!
Thanks! And it is a relief to be able to write LaTeX in posts.
Very nice article, I wasn’t aware of the other examples yet.
And thanks for the flowers! By the way, I thought everyone likes convolutions, disliking them would be like disliking Surströmming, wouldn’t it? 😉
Thanks!
Well, both take a while to learn to get used to. And the “smell” of the formula might scare people away while the “taste” of how it is used is quite different.