Uriel’s stacking problem

Reading angelIn Scott Alexander’s kabbalistic sf story Unsong, the archangel Uriel works on a problem while other things are going on in heaven:

All the angels listened in rapt attention except Uriel, who was sort of half-paying attention while trying to balance several twelve-dimensional shapes on top of each other.
…
There was utter silence throughout the halls of Heaven, except a brief curse as Uriel’s hyperdimensional tower collapsed on itself and he picked up the pieces to try to rebuild it.
…
A great clamor arose from all the heavenly hosts, save Uriel, who took advantage of the brief lapse to conjure a parchment and pen and start working on a proof about the optimal configuration of twelve-dimensional shapes.

(Chapter 20, When the stars threw down their spears)

A polytope on a plane

This got me thinking about the stability of stacking polytopes. That seemed complicated (I am no archangel) so I started toying with the stability of polytopes on a flat surface.

(Terminology note: I will consistently use “face” to denote the D-1 dimensional elements that bound the polytope, although “facet” is in some use.)

A face of a 3D polyhedron is stable if the polyhedron can rest on it without tipping over. This means that the projection of the center of mass onto the plane containing the face is inside the polygon. The platonic polyhedra are stable on all faces, but it is not hard to make a few faces unstable by moving a vertex far away from the center. A polyhedron has at least one stable face (if it did not, it would be a perpetual motion device: every tip will move the center of mass downwards, but there is a bound on how low it can go. A uni-stable or monostatic polyhedron has  just one stable face. It is an unsolved problem what the simplest uni-stable 3D polyhedron is, with the current record 14 faces. Also, it seems unclear whether there are monostatic simplices in dimension 9 (they exist in 10 or more dimensions, but not in 8 or fewer).

So, how many faces of a polytope will typically be unstable?

I wrote a Matlab script to generate random convex polytopes by selecting N points randomly on the surface of a D-dimensional sphere and calculating their convex hull. Using a Delaunay decomposition I can split them into simplices, which allow me to calculate the center of mass. The center of mass of a simplex is just the average of the corners \vec{x^c_j}=\sum_{i=1}^N \vec{x}_{ij}, and the center of mass of the polyhedron is just the sum of the simplex centers of mass weighted by their volumes: \vec{x^p} = \sum_{j=1} V_j \vec{x^c_j} . The volume of a simplex is V_j=(1/D!)\mathrm{det}(X_j) where X_j=[x_{1j};x_{2j};\ldots;x_{Dj}], the matrix made by sticking together the coordinate vectors of a simplex. Once we know this we can project the center of mass onto the plane of a face by finding its nullspace (the higher dimensional counterpart to a normal) \vec{p}= \vec{x^p} -(\vec{x^p}\cdot \vec{n})\vec{n}. Finally, to check whether the projection is inside the face, we can look at the matrix A where each column is the coordinates of one of the faces minus \vec{p} and the final row just ones, and solve for Ax=b where b is zero except for a one in the last row (I found this neat algorithm due to elisbben on stack overflow).  If the answer vector is all positive, then the point is inside the face. Repeat for all the faces.

Whew. This math is of course really simple to do in Matlab.

Stable (yellow) and unstable (blue) faces of random polyhedron.
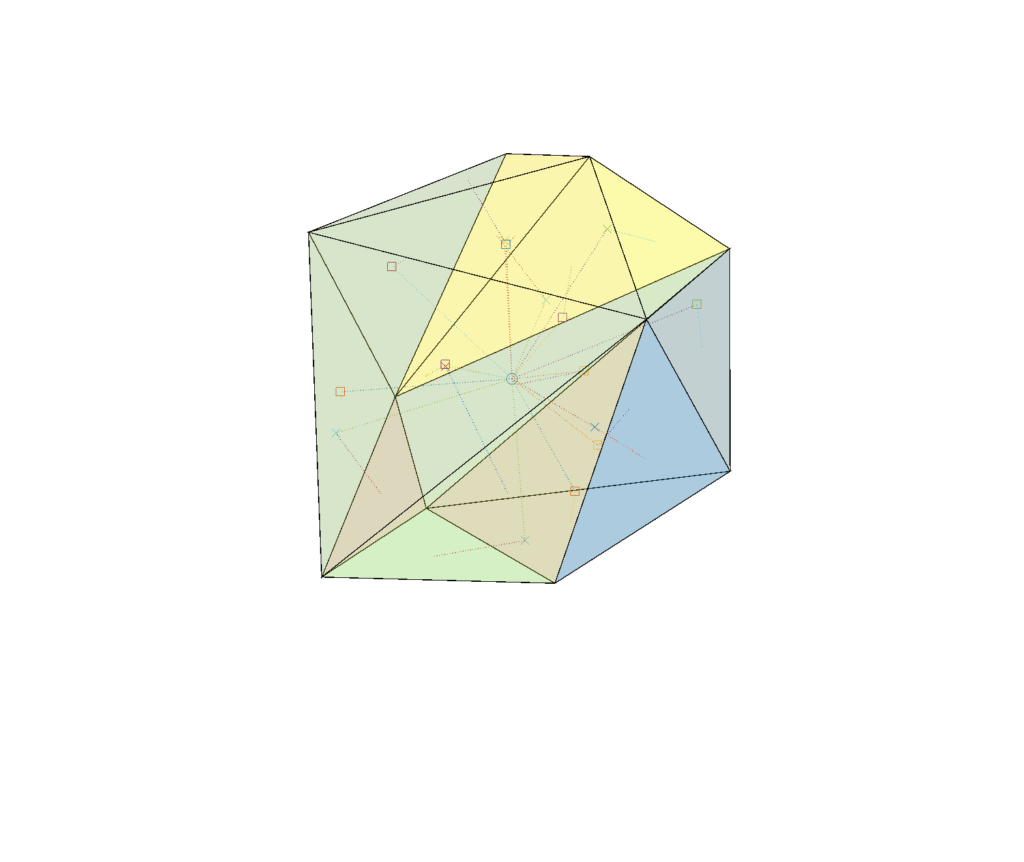
Stability of random polyhedron. The center of mass is marked by a circle. It is projected along the dotted lines into the plane of each face, marked with a square (if inside the face and hence a stable face) or a cross (if outside the face, which is hence unstable). A dotted line connects the projection points to the center of their face.
Stability of random polyhedron. The center of mass is marked by a circle. It is projected along the dotted lines into the plane of each face, marked with a square (if inside the face and hence a stable face) or a cross (if outside the face, which is hence unstable). A dotted line connects the projection points to the center of their face.

The 12 dimensional case is a bit messier:

Projection of a 12D polytope with 20 vertices. Each face is a 11 dimensional simplex.
Projection of a 12D polytope with 20 vertices. Each of the 2777 faces is a 11 dimensional simplex.

So, what is the average fraction of stable faces on a 3D polyhedron?

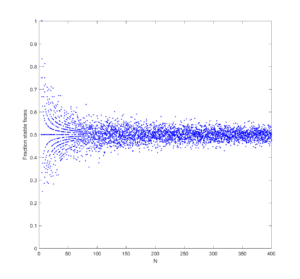
Fraction stable faces on 3D convex hulls of N points on a sphere.
Fraction stable faces on 3D convex hulls of N points on a sphere.

It tends to converge to 50%. Doing this in higher dimensions shows the same kind of convergence, although to lower fractions.

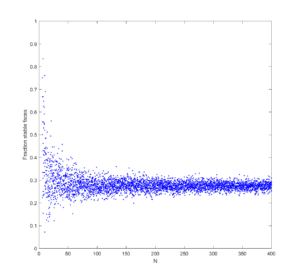
Fraction stable faces on 4D convex hulls of N points on a sphere.
Fraction stable faces on 4D convex hulls of N points on a sphere.
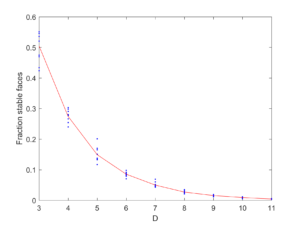
Fraction stable faces of N=100 convex hulls in different dimensions. Red line exponential fit.
Fraction stable faces of N=100 convex hulls in different dimensions. Red line exponential fit.

It looks like the fraction of stable faces declines exponentially with dimensionality.

Does this mean that for a sufficiently high dimension it is likely that a random polytope is unistable? The answer is no: the number of faces increases pretty exponentially (as 2^{1.7680D}), but the number of stable faces also increases exponentially with D (as $latex 2^{0.9273 D}$).

Combined plot of number of faces (points with red line) and stable faces (points with green line) as a function of dimension for N=100.
Combined plot of number of faces (points with red line) and stable faces (points with green line) as a function of dimension for N=100.

This was based on runs with N=100. Obviously things go much faster if you select a lower N, such as 30. However, as you approach N=D the polytopes become more and more simplex-like, and simplices tend to both have fewer faces and be less stable in high dimensions, so the exponential growth stops. This actually happens far below D; for N=30 the effect is felt already in 11 dimensions. The face growth rates were also lower, with coefficients 1.1621 and 0.4730.

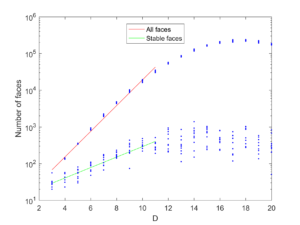
Number of faces and stable faces for N=30 random convex hulls in different dimensions.
Number of faces and stable faces for N=30 random convex hulls in different dimensions.

(There are some asymptotic formulas known for the growth of the number of faces for random convex hulls; they grow linearly with N but at an accelerating rate with D.)

Stuart Armstrong gave me a very heuristic argument for why there would be so many unstable faces. Consider building up the polytope vertex by vertex, essentially just adding together the simplices from the Delaunay decomposition. If you start from a stable state, eventually you will likely end up with an unstable face. Adding the next vertex will add a simplex to the polyhedron, and the center of mass will move in the direction of the new simplex. To have the face become stable again the shift in center of mass needs to be large enough along the directions parallel to the face to bring the projection back inside the face. But in high dimensional spaces there are many directions you can move in: the probability of a random vector being nearly parallel to another vector is very low. Hence, the next step and the following are likely to preserve the instability. So high dimensional polytopes are likely to have many unstable faces even if they are nicely inscribed in spheres.

The number of steps the polytope rolls over  until finding a stable face is also limited: the “drainage basin” of a stable face is a tree, with a branching degree set by D-1 (if faces are D-simplexes). So the number of steps will scale as \log_{D-1}(2^{(1.7680 - 0.9273)D})=0.8407 D \ln(2) / \ln(D-1) \propto D/\ln(D). Even high-dimensional polytopes will stop flipping quickly in general. (A unistable polytope on the other hand can run through at least half of its faces, so there are some very slow ones too).

The expected minimum distance between two points on this kind of random polytope scales as N^{-2/D} (if they were optimally distributed it would be N^{-1/D}). At the same time, if N is relatively small compared to D (the polytope is simplex-like), the average diameter (the longest edge) of each face seems to approach \sqrt{\pi}. Why? I think this is because  \Gamma(1/2), the mean of a flipped k=2 Weibull distribution that shows up because of extreme value theory. Meanwhile the average and median cord length between random points on hyperspheres tends towards \sqrt{2}. Faces hence tends to be fairly wide unless N is large compared to D, but there will typically always be a few very narrow ones that are tricky to balance on.

Stacking no-slip polytopes

What about stacking polytopes?

If you put a polytope on top of another one (assuming no slipping) at first it seems you need to use a stable face of the top polytope, but this is not enough nor necessary.

Since the underlying face is likely tilted from the horizontal, the vertical projection of the center of mass has to be within the top face. The upper polytope can be rotated, moving the projection point. The tilt angle \theta (or rather, tilt angles – we are doing this in higher dimensions, remember?) generates a hypersphere of radius d \tan(\theta) around the normal projection point (which is at distance d from the center of mass) where the vertical projection can intersect the face. Only parts of the hypersphere surface that are inside the face represent orientations that are stable. Even an unstable face can (sometimes) be stabilized if you turn it so that the tilted projection is inside, but for sufficiently high angles the hypersphere will be bigger than the face and it cannot be stable.

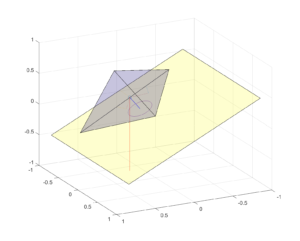
Stability of polyhedron on tilted surface. The line of gravity from the center of mass intersects the inside the bottom face, so the polyhedron is resting stably. Turning the polyhedron will move the line to some point on the circle, but since all points on the circle are inside the face all orientations are stable.
Stability of polyhedron on tilted surface. The line of gravity from the center of mass intersects the inside the bottom face, so the polyhedron is resting stably. Turning the polyhedron will move the line to some point on the circle, but since all points on the circle are inside the face all orientations are stable.
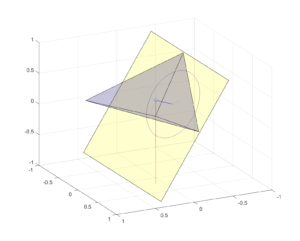
Stability of polyhedron on tilted surface. The line of gravity from the center of mass intersects the outside the bottom face, so the polyhedron is unstable and will flip over. Turning the polyhedron will move the line to some other point on the circle: since some points on the circle are inside the face there are some orientations that are stable.
Stability of polyhedron on tilted surface. The line of gravity from the center of mass intersects the outside the bottom face, so the polyhedron is unstable and will flip over. Turning the polyhedron will move the line to some other point on the circle: since some points on the circle are inside the face there are some orientations that are stable.

Having the top polytope stay in place is the first requirement. The second is that the bottom polytope should not become unstable. The new center of mass is moved to a point somewhere along the connecting line between the individual centers of mass of the polytopes, with exact position dependent on their volume ratio (note that turning the top polytope can move the center of mass too). This moves the projection point along the plane of the bottom face, and if it gets outside that face the assembly will tip over.

One can imagine this as adding random (D-1)-dimensional vectors of length 1/N until they reach the edge of the face. I am a bit uncertain about the properties of such random walks (all works on decreasing step size walks I have seen have been in 1D). The harmonic random walk in 1D apparently converges with probability 1, so I think the (D-1)-dimensional one also does it since the distance from the origin to the walker will be smaller than if the walker just kept to a 1D line. Since the expected distance traversed in 1D is $latex E[|X|] \approx 1.0761$ this is actually not a very extreme  shift. Given the surprisingly large diameters of the faces if N \ll D the first condition might be tougher to meet than the second, but this is just a guess.

The no slipping constraint is important. If the polytopes are frictionless, then any transverse force will move them. Hence only polytopes that have some parallel top and bottom stable faces can be stacked, and the problem becomes simpler. There are still surprises there, though: even stacks of rectangular blocks can do surprising things. The block stacking problem also demonstrates that one can have 1/N overhangs (counting downwards), enabling arbitrarily large total overhangs without tipping over. With polytopes with shapes that act as counterweights the overhangs can be even larger.

Uriel’s stacking problems

This leads to what we might call “Uriel’s stacking problem”: given a collection of no-slip convex D-dimensional polytopes, what is the tallest tower that can be constructed from them?

I suspect that this problem is NP-hard. It sounds very much like a knapsack problem, but there is a dependency on previous steps when you add a new polytope that seem to make it harder. It seems that it would not be too difficult to fool a greedy algorithm just trying to put the next polytope on the most topmost face into adding one that makes subsequent steps too unstable, forcing backtracking.

Another related problem: if the polytopes are random convex hulls of N points, what is the distribution of maximum tower heights? What if we just try random stacking?

And finally, what is the maximum overhang that can be done by stacking polytopes from a given set?

Crystal boutique

2 thoughts on “Uriel’s stacking problem”

  2. Pingback: Hexbyte Hacker News Computers SSC Journal Club: Dissolving The Fermi Paradox | HexByte Inc.

Leave a Reply

Your email address will not be published. Required fields are marked *