I like the hyperbolic tangent function. It is useful for making sigmoid curves for neurons and fitting growth rates, it enables a cute minimal surface. So of course it should be iterated to make fractals! And there is no better way to celebrate Newtonmass than to make fractals!
As iteration formula I choose , where c is a multiplicative constant. Iterating some number like 1 and plotting its fate produces the following “Mandelbrot set” in the c-plane – the colours here do not denote the time until escape to infinity but rather where in the complex plane the point ended up, as a function of c. In a normal Mandelbrot set infinity is an attractive fixed point; here it is just one place in the (extended) complex plane like any other.
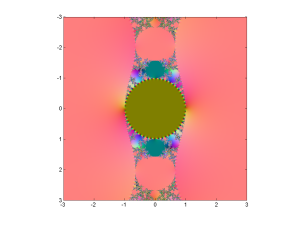
The pinkish surroundings of the pattern represent points attracted to the positive solution of . There is of course a corresponding negative solution since tanh is antisymmetric: if z is an attractive fixed point or cycle, so is -z. So the dynamics is always bistable.
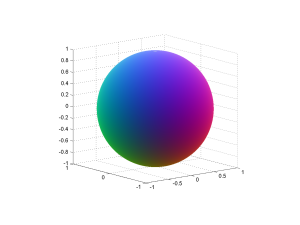
Incidentally, the color scheme is achieved by doing a stereographic projection of the complex plane onto a sphere, which is then fitted into the RBG cube. Infinity corresponds to (0.5,0.5,1) and zero to (0.5,0.5,0) – the brownish middle of the Mandelbrot set, where points are attracted towards zero for small c.
Another property of tanh is that the function has singularities wherever for integer
. Since Great Picard’s Theorem, that means that in the vicinity of those points it takes on nearly all other values in the complex plane. So whatever the pattern of the corresponding Julia set is, it will repeat itself near there (including images of the image, and so on).This means that despite most z points being attracted towards zero for c-values inside the unit circle, there will be a complex stitching of undefined points since they will be mapped to infinity, or are preimages of points that get mapped there.
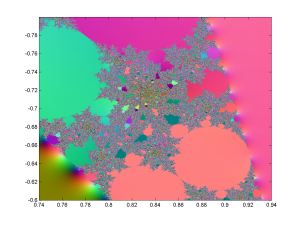
Zooming into the messy regions shows that they are full of circle-cusp areas where there is a periodic attractor cycle. Between them are the regions where most of the z-plane where the Julia sets live is just pure chaos. Thanks to various classic theorems in the theory of complex iteration we know that if the Julia set has non-empty interior it is the entire complex plane.
Walking around the outside edge of the boring brown circle gives a fun sequence of patterns. At there are two real fixed points and a straight line border along the imaginary axis. This line of course contains the singularity points where things get sent to infinity, and near them the preimages of all the other singularities on the line: dramatic, but visually uninteresting.

As we move along the circle towards more imaginary c, there is a twisting of the border since each multiplication by c corresponds to a twist: it is now a fractal spiral covered by little spirals. As the twisting gets stronger, the spirals get bigger and wilder (especially when we are very close to the unit circle, where the dynamics has a lot of intermittency: the iterates almost but not quite gets stuck close to certain points, speed away, and then return to make rather elliptic spirals).



When we advance towards a cuspy border in the c-plane we see the spirals unfold into long twisty tentacles just before touching, turning into borders between chains of periodic domains.

But then the periodic domains start to snake out, filling the plane wildly.

until we get a plane-filling, ergodic Julia set with no discernible structure. For some c-values there are complex tesselations of basins of attraction, and quite often some places are close enough to weakly repelling fixed points to produce small circular false basins of attraction where divergence is slow.

One way of visualizing this is to make a bifurcation diagram like we do for real iteration. Following a curve we plot where iterates end up projected along some line (for example their real or imaginary part, or some combination). To make structure stand out a bit more I decided to color points after where in the whole plane they are, producing a colorful diagram for r=1.1:
(I have some others on Flickr for the imaginary axis, r=1.25 and r=1.5).
Another, more fun way is to turn them into animated gifs. Since Flickr doesn’t handle them well, I have stored them locally instead:
- Growth of the Mandelbrot set – shows the behaviour of test iterates in the c-plane near the edge. Note the intermittent spirals.
- Unit circle – following the unit circle.
- Tanh 1.0 – the same as above, but inverted coordinates:
is at the center, zero outside the borders.
- Tanh 1.1 – r=1.1.
- Tanh 1.5 – r=1.5.
- Tanh 2.5 – r=2.5.
- Tanh 5.0 – r=5.0. Rather sedate except for a brief window near
.
Note how spirals unfold until they touch each other, forming periodic domains or exploding across the entire plane, making a chaotic full-plane attractor… which often blinks into complex patterns of periodic domains only to return to chaos.


