 Most of the time we encounter probability distributions over the reals, the positive reals, or integers. But one can use the rational numbers as a probability space too.
Most of the time we encounter probability distributions over the reals, the positive reals, or integers. But one can use the rational numbers as a probability space too.
Recently I found the paper Vladimir Trifonov, Laura Pasqualucci, Riccardo Dalla-Favera & Raul Rabadan. Fractal-like Distributions over the Rational Numbers in High-throughput Biological and Clinical Data. Scientific Reports 1:191 DOI: 10.1038/srep00191. They discuss the distribution of ratios of the number of reads from the same spot of DNA that come from each chromosome in a pair: the number of reads is an integer, so the ratio is rational. They get a peaky, self-similar distribution empirically, and the paper explains why.
If you take positive independent integers from some distribution and generate ratios
, then those ratios will have a distribution that is a convolution over the rational numbers:
One can of course do the same for non-independent and different distributions of the integers. Oh, and by the way: this whole thing has little to do with ratio distributions (alias slash distributions), which is what happens in the real case.
The authors found closed form solutions for integers distributed as a power-law with an exponential cut-off and for the uniform distribution; unfortunately the really interesting case, the Poisson distribution, doesn’t seem to have a neat closed form solution.
In the case of a uniform distributions on the set they get
.
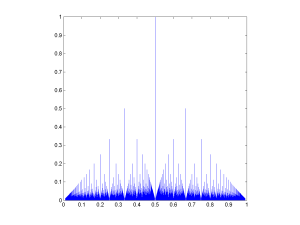
They note that this is similar to Thomae’s function, a somewhat well-known (and multiply named) counterexample in real analysis. That function is defined as f(p/q)=1/q (where the fraction is in lowest terms). In fact, both graphs have the same fractal dimension of 1.5.
It is easy to generate other rational distributions this way. Using a power law as an input produces a sparser pattern, since the integers going into the ratio tend to be small numbers, putting more probability at simple ratios:
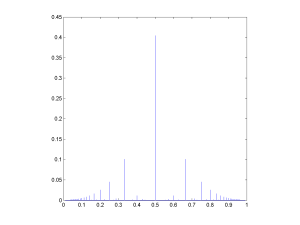
If we use exponential distributions the pattern is fairly similar, but we can of course change the exponent to get something that ranges over a lot of numbers, putting more probability at nonsimple ratios where
:
![The rational distribution of two convolved Exp[0.1] distributions.](http://aleph.se/andart2/wp-content/uploads/2014/09/trifonovexp01-300x225.png)
![Rational distribution of ratio between a Poisson[10] and a Poisson[5] variable.](http://aleph.se/andart2/wp-content/uploads/2014/09/trifonovpoiss105-300x225.png)
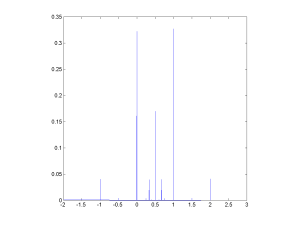
But multiplying the variates by 10 produces a nice distribution.
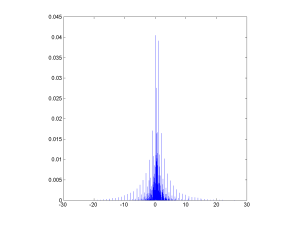
This approaches the Chauchy distribution as the discretisation gets finer. But note the fun microstructure (very visible in the Poisson case above too), where each peak at a simple ratio is surrounded by a “moat” of low probability. This is reminiscent of the behaviour of roots of random polynomials with integer coefficients (see also John Baez page on the topic).
The rational numbers do tend to induce a fractal recursive structure on things, since most measures on them will tend to put more mass at simple ratios than at complex ratios, but when plotting the value of the ratio everything gets neatly folded together. The lower approximability of numbers near the simple ratios produce moats. Which also suggests a question to ponder further: what role does the über-unapproximable golden ratio have in distributions like these?
Oh shit, is this what you’ve meant by “rationality” all along?
Is there any other meaning?