I recently came across this nice animated gif of a fractal based on a Steiner chain, due to Eric Martin Willén. I immediately wanted to replicate it.
Make Steiner chains easily
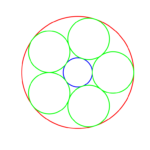
First, how do you make a Steiner chain? It is easy using inversion geometry. Just decide on the number of circles tangent to the inner circle (). Then the ratio of the radii of the inner and outer circle will be
. The radii of the circles in the ring will be
and their centres are located at distance
from the origin. This produces a staid concentric arrangement. Now invert with relation to an arbitrary circle: all the circles are mapped to other circles, their tangencies preserved. Voila! A suitably eccentric Steiner chain to play with.
Since the original concentric chain obviously can be rotated continuously without losing touch with the inner and outer circle, this also generates a continuous family of circles after the inversion. This is why Steiner’s porism is true: if you can make the initial chain, you get an infinite number of other chains with the same number of circles.
Iterated function systems with circle maps
The fractal works by putting copies of the whole set of circles in the chain into each circle, recursively. I remap the circles so that the outer circle becomes the unit circle, and then it is easy to see that for a given small circle with (complex) centre and radius
the map
maps the interior of the unit circle to it. Use the ease of rotating the original concentric ring to produce an animation, and we can reconstruct the fractal.
Done.
Except… it feels a bit dry.
Ever since I first encountered iterated function systems in the 1980s I have felt they tend towards a geometric aesthetics that is not me, ferns notwithstanding. A lot has to do with the linearity of the transformations. One can of course add rotations, which cheers up the fractal a bit.
But still, I love the nonlinearity and harmony of conformal mappings.
Inversion makes things better!
Enter the circle inversion fractals. They are the sets of the plane that map to themselves when being inverted in any and all of a set of generating circles (or, equivalently, the limit set of points under these inversions). As a rule of thumb, when the circles do not touch the fractal will be Cantor/Fatou-style fractal dust. When the circles are tangent the fractal will pass through the point of tangency. If three circles are tangent the fractal will contain a circle passing through these points. Since Steiner chains have lots of tangencies, we should get a lot of delicious fractals by using them as generators.
I use nearly the same code I used for the elliptic inversion fractals, mostly because I like the colours. The “real” fractal is hidden inside the nested circles, composed of an infinite Apollonian gasket of circles.
Note how the fractal extends outside the generators, forming a web of circles. Convergence is slow near tangent points, making it “fuzzy”. While it is easy to see the circles that belong to the invariant set that are empty, there are also circles going through the foci inside the coloured disks, touching the more obvious circles near those fuzzy tangent points. There is a lot going on here.
But we can complicate things by allowing the chain to slide and see how the fractal changes.
This is pretty neat.







Hello,
i´ve a question but it somehow touches this topic too. It´s about your recent article “Dissolving the Fermi-Paradox”. I´ve been wondering where the fractals are in Einstein`s field equasion. I mean we´ve found them pretty much in every field but not there as far as my limited understanding of the matter goes.
As far as i get it we´re basically looking for Dyson-Swarms to infere whether we´re alone right? So if there are fractals in spacetime geometry would this enable FTL travel? Would we be able to detect an ETI who´s using FTL travel?
Luckily we´re all pretty much clueless so i´m not this much bothered by me asking such naive questions.
The Einstein equations are differential equations, so they presuppose a smooth spacetime – no fractals there. You get chaotic orbits in many cases, like around merging black holes – accurate pictures of them will show fractal patterns due to multiple images as light is wrapping around the horizons.
There is no real reason to think fractals have anything to do with FTL. Just because one thing is cool doesn’t mean it has to be involved with other cool mysteries.
Oh i thought fractals are part of geometry and i read something about space time geometry as well so i believed the two are related. My fault. Ayways thanks for answering.
I have other questions:
Is the Plank lengh kind of a “natural” barrier preventing fractals in spacetime geometry?
Wiki says “…beyond (or below) which the predictions of the Standard Model, quantum field theory and general relativity are no longer reconcilable…” So it´s not a hard barrier, we just cannot know, or am i wrong again?
Is this “hologram” universe fractal in nature? Does the Hausdorf-Dimension have some kind of expression beyond math? Can we know whether this “higher dimension” required is a fractal?
Forgive my reference of wiki but i´m kind of clueless about the whole math. I´m just a bit curious and fascinated by these fractals.
Your animations reminded of some work that I did several years ago. An example is shown at https://www.pinterest.com/pin/405324035191340536/. What you see here is a fractal tiling, in which each circle is smaller than the last in such a way that there’s always room for one more. I call this Tim Burton’s Cartesian Nightmare. At any rate, you’ve done some nice work here.